S2OJ NOIP 模拟赛3 div2 题解合集

原题：

A

求什么就对什么计数。寻找合法解的条件。

考虑寻找集合合法的条件，为了方便考虑，我们将集合中元素从小到大排序。

假设目前考虑到了集合中的元素 \(a_i\)，因为我们要求集合能够表示 \([0,\sum_{j=1}^i a_j]\) 中的所有元素，所以 \([0,\sum_{j=1}^{i-1} a_j]\) 需要能够被前 \(i-1\) 个元素表示，同时需要满足 \(a_i \le \sum_{j=1}^{i-1} a_i+1\)，否则会出现 \((\sum_{j=1}^{i-1} a_j,a_i]\) 无法被表示的情况。

于是我们得到了集合合法的充要条件：

\[\forall i,a_i\le \sum_{j=1}^{i-1} a_j+1 \]

现在考虑 DP，设 \(f_{i,j}\) 表示现在从小往大考虑到第 \(i\) 个元素，\(\sum a=j\) 的合法集合数。

令 \(m=\max_{i=1}^n a_i\)，转移是简单的：

\[f_{i,j} \to f_{i+1,\min(j+a_{i+1},m)},a_{i+1}\le j+1 \]

复杂度 \(O(n^2)\)。

B

看到决策一个排列，大概率和邻项微扰相关。

不难想到一个贪心策略：

• 对于 \(c_i\le w_i\) 的情况，此时打怪兽加血，我们按 \(c_i\) 从小到大排序，把加血的放在最前面即可；

• 对于 \(c_i>w_i\) 的情况，此时打怪兽扣血，我们考虑邻项微扰：

对于相邻两项 \(i,j\)，\(i\) 在 \(j\) 前，我们希望最大化：

\[\min(c_i,c_i-w_i+c_j) \]

经过推导得知按 \(w_i\) 从大到小排序最优。

复杂度 \(O(n \log n)\)。

C

看到 \(n\) 只有 \(400\)，我们考虑不决策怎么交换，而是决策最终序列长什么样，计算交换次数。

设 \(f_{i,a,b,0/1/2}\) 表示考虑前 \(i\) 个位置，填了 \(a\) 个 \(0\)，\(b\) 个 \(1\)，第 \(i\) 位填了 \(0/1/2\) 的最小交换次数。

不难发现此时填了 \(c=i-a-b\) 个 \(2\)，我们不记进状态里。

现在的问题在于怎么算交换次数，也就是我们需要求出，在之前填了 \(a\) 个 \(0\)，\(b\) 个 \(1\)，\(c\) 个 \(2\)，在这一位填 \(0/1/2\)，需要在这一位的交换次数。

填 \(0/1/2\) 的情况是类似的，我们只考虑 \(0\) 的情况。

我们可以找出原串中第 \(a+1\) 个 \(0\) 的位置，记为 \(p\)，在之前 \(i-1\) 位不断交换交换，只会把 \(p\) 之后的 \(1,2\) 换到 \(p\) 之前，设 \(p\) 之前有 \(b',c'\) 个 \(1,2\)，那么容易求出 \(p\) 在现在真正的位置 \(p'=p+\max(0,b-b)+\max(0,c-c')\)。

那么交换的次数就是 \(p'-i\)。

直接 DP，复杂度 \(O(n^3)\)。有点卡空间，滚动数组之。

D

常规看不懂题解在说啥，只是发现题解码长比自己长一倍。（1/1）

md 所以题解在说啥啊？？？

首先将题意转化为，在长度为 \(n\) 的序列中选若干个数，要求间隔至少为 \(k\)，最大化选数的和。

考虑简单 DP，设 \(f_{i}\) 表示考虑前 \(i\) 个位置的最大答案，容易得到转移：

\[f_i=\max(f_{i-1},f_{i-k}+a_i) \]

考虑将 DP 数组按 \(\bmod k\) 同余分组，另设 \(g_{i,j}=f_{ik+j}\)，在线段树上每个位置维护 \(g_{*,j}\)，\(*\) 的值取决于目前 DP 到的连续段位置。

从小往大考虑每个极长连续段 \((l,r,k)\)，它在线段树上长这样：

橙色的是具体的连续段，黑色的是原序列。

每次我们在线段树上，维护的具体 DP 值是：

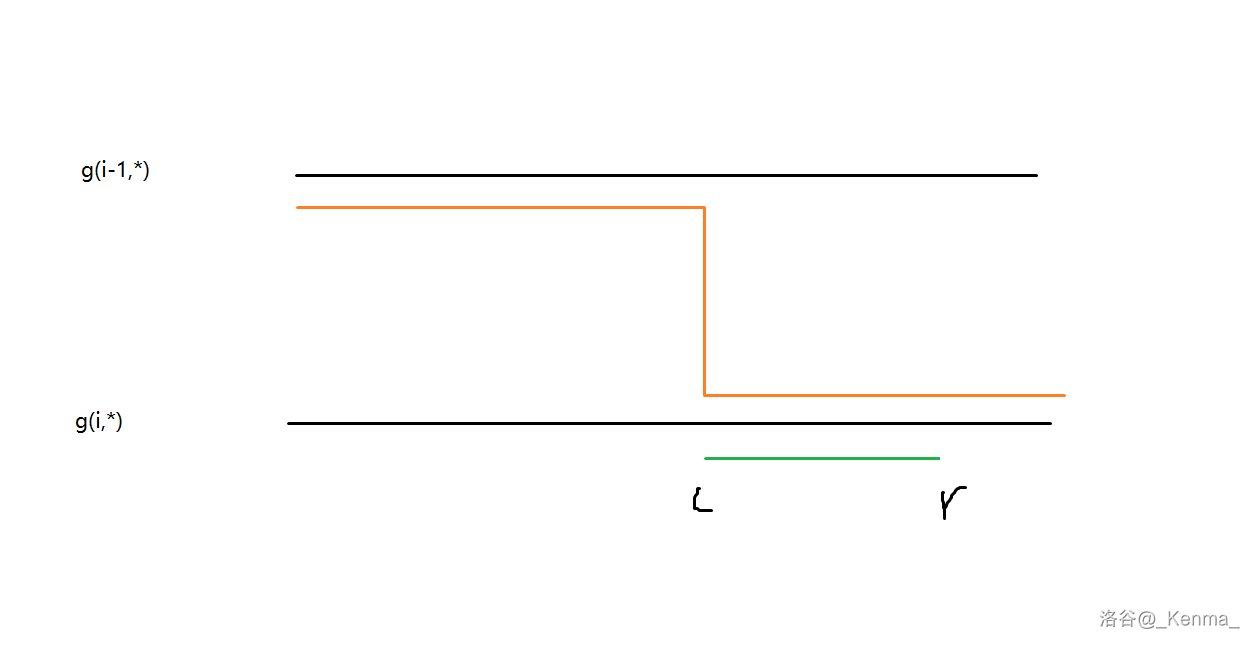
橙色的是线段树上的节点代表什么，绿色的是当前转移的连续段。

首先考虑 \(f_{i-k}\to f_i\) 的转移。

考虑两头的区间，我们只需要在对应区间上做区间加 \(k\) 即可。

对于中间的区间，因为我们都是全局加，所以我们直接把加 \(k\) 累加到答案中，不需要再在线段树上修改。

然后考虑 \(f_{i-1} \to f_i\) 的转移。

我们发现我们难以转移，但是又发现，贪心地考虑，我们只需要在区间左端点维护这个前缀 \(\max\)，在别的地方忽视 \(f_{i-1} \to f_i\) 的转移即可。理由很简单，我们在同一个连续段内加的 \(k\) 的值相同，相对靠左的位置如果 DP 值还大，那么相对靠右的区间完全不用理会。

这一部分只需要在线段树上查询上一个连续段区间的最大值，然后在当前连续段的 \(l\) 位置单点取 \(\max\) 即可。

具体的维护方式下午详细说明。

复杂度 \(O(m \log m)\)。