题解：P12543 [APIO2025] 转杆

前言

详细解密为什么我过 T3 没有 Ag。

思路分析

首先这个题面太唬人了，但是读完发现和计算几何啥的没关系。

考虑末态，不难发现是线段两两配对垂直，此时答案是 \(25000(\lfloor\frac{n}{2}\rfloor)^2\)。

于是考虑构造合法操作方案使得答案不降。

有一个想法是，以和 \(x\) 轴角度最小的直线为新的 \(x\) 轴建立坐标系，然后依次旋转直线使得所有直线和坐标轴平行，最后再调整使得和 \(x\) 轴平行和 \(y\) 轴平行的直线数的差小于等于 \(1\)。

然后考虑什么时候直线可以被旋转至和坐标轴平行。

我们建立新的坐标轴之后，图上的直线可以分为四类，如图所示：

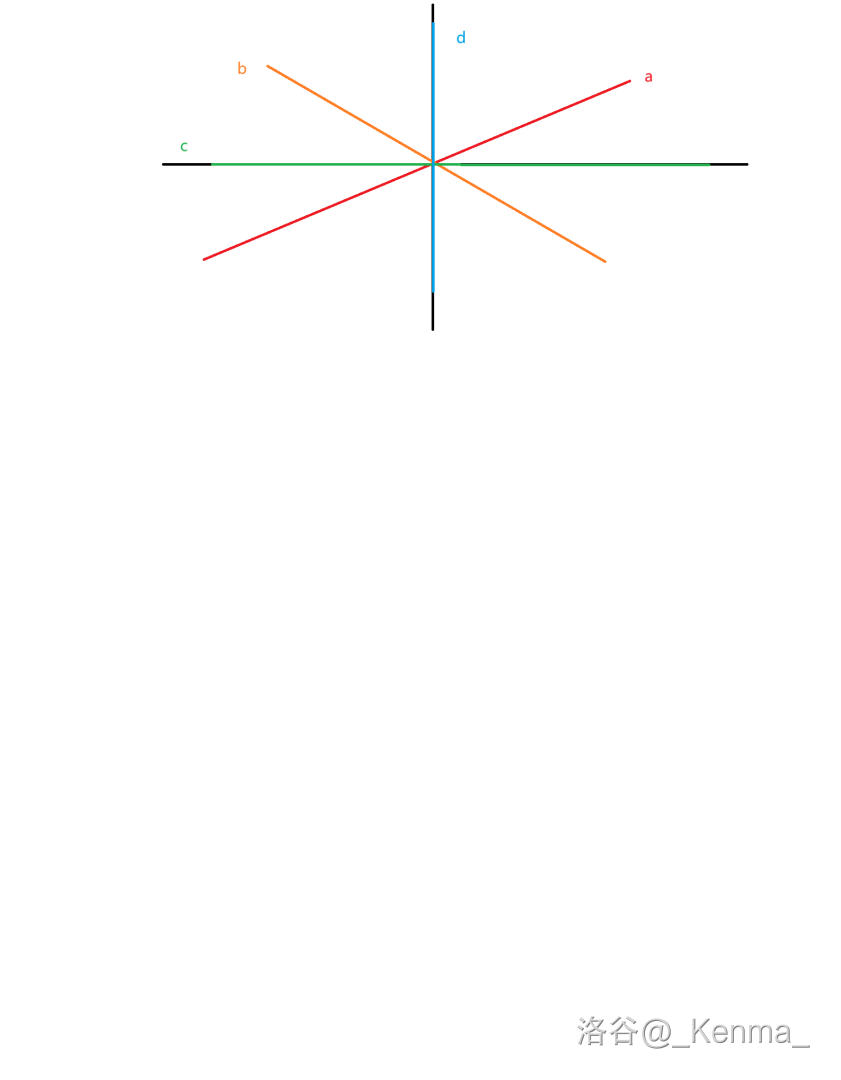
考虑什么时候可以旋转什么样的直线：

• \(a+c>b+d\)，旋转 \(a\) 中最靠近 \(d\) 的直线至 \(d\)；

• \(a+c<b+d\)，旋转 \(b\) 中最靠近 \(c\) 的直线至 \(c\)；

• \(a+d>b+c\)，旋转 \(a\) 中最靠近 \(c\) 的直线至 \(c\)；

• \(a+d<b+c\)，旋转 \(b\) 中最靠近 \(d\) 的直线至 \(d\)。

因为每次都是 \(a,b\) 移动到 \(c,d\)，所以移动会在有限次内结束。

无法移动的情况可能有两种：

• \(a=b\) 且 \(c=d\)；

• 满足不等式但是 \(a=0\) 或 \(b=0\)。

仔细思考后发现第二种是不可能的，此时除非 \(a=b=0\)，不然一定存在满足条件的移动方式。

于是我们只需要考虑第一种情况的处理，因为此时满足 \(c=d\)，相当于之前移动的直线已经两两配对，我们只需要把剩下 \(a,b\) 中的直线两两配对即可。这个部分是简单的，仔细手玩之后发现只需要把 \(a\) 中最靠近 \(d\) 的直线和 \(b\) 中最靠近 \(c\) 的直线配对即可，依次进行，判断谁去向谁垂直，就能做到每次移动直线都不相交。

如果没有出现第一种情况，那么一定能移动至 \(a=b=0\) 的末态，此时我们再调整 \(c,d\) 的值使得 \(|c-d|\le 1\) 即可。

使用 set 维护直线斜率，复杂度 \(O(n \log n)\)，操作次数在 \(1.5n\) 以内。

后记

这个做法其实属于比较麻烦的那种，所以场上我刚了 4h 才刚出来，导致 T1 T2 暴力基本没打，Cu 遗憾离场。

有无老哥帮我复现一下代码。