题解：AT_abc283_g [ABC283G] Partial Xor Enumeration

abc283_g 解题报告

前言

首先这个题面就很抽象。

其实就是求序列任意数的异或和中，第 \(l\) 小到第 \(r\) 小的数。

思路分析

其实是模板题。

考虑线性基可以求异或第 \(k\) 小，直接循环枚举 \([l,r]\)，直接求就行了。

复杂度 \(O(n \log v)\)。

所以这篇题解主要讲线性基为什么能以及怎样求异或第 \(k\) 小。

首先其实我们写的最多的，从高位到低位贪心插入的线性基并没有很好的性质。

比如说，线性基中的一个元素 \(a_i\)，只能满足它的最高位是 \(i\)，但是对它的低位并没有限制，也就是说，它不是所有可能的 \(a_i\) 中最小的一个。

考虑这样修改我们贪心构建的线性基。

对于每一个线性基中的元素 \(a_i\)，枚举它在线性基中的所有低位元素 \(a_j\)，将 \(a_i\) 异或上 \(a_j\)，以此消去 \(a_i\) 的低位 \(1\)。这样 \(a_i\) 依然是合法的，但是 \(a_i\) 变成了所有可能的 \(a_i\) 中最小的一个。

值得一提的是，这样依次消去 \(a_i\) 的低位 \(1\) 的操作和高斯消元构建线性基的本质是相同的。因为消去低位 \(1\) 的过程也可以被理解为构建上三角矩阵。

这样重新构建的线性基就有了很好的性质。

不难发现，这样构造，使得线性基中的每一个元素 \(a_i\)，有且只有它在第 \(i\) 位上是 \(1\)。

可能文字还是比较苍白，上图：

放错了。

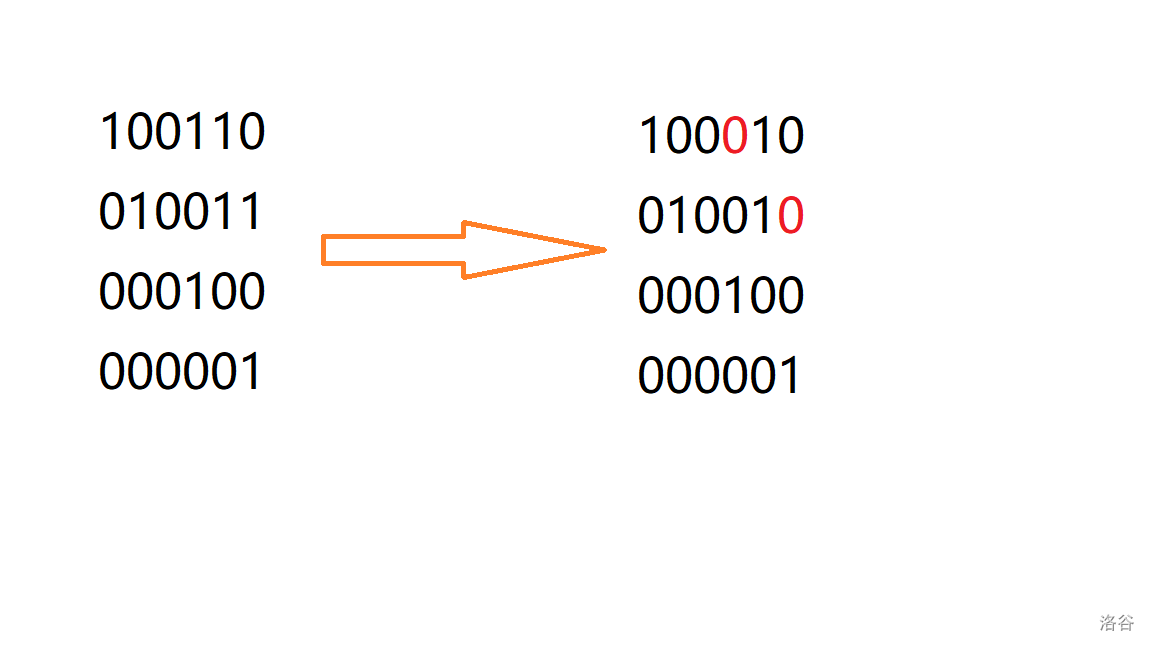
这张是对的。

从左往右由高到低，和高斯消元的结果应该是一样的。

然后考虑怎样求第 \(k\) 小。

注意到调整后线性基中的元素只会越异或越大，并且越高位的线性基，它和别人异或的结果会严格大于它不参与异或的结果。

所以第 \(k\) 小元素就是将 \(k\) 二进制拆分后，选择 \(k\) 这一位是 \(1\) 的若干个线性基中的元素异或起来的结果。

比如求上图的线性基的异或第 \(3\) 小值，应该让第三个元素和第四个元素异或，结果是 \(5\)。

具体实现看代码。

代码实现

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,l,r,a[200005];
int base[65],flag;
void insert(int a){
	for(int i=61;i>=1;i--){
		if(a&(1ll<<(i-1))){
			if(base[i]) a^=base[i];
			else{
				base[i]=a;
				break;
			}
		}
	}
	flag=1;
}
void rebuild(){
	for(int i=1;i<=61;i++){
		for(int j=1;j<i;j++){
			if(base[i]&(1ll<<(j-1))) base[i]^=base[j];
		}
	}
}
int query_k(int k){
	int ans=0;
	k-=flag;
	if(!k) return 0;
	for(int i=1;i<=61;i++){
		if(base[i]){
			if(k&1) ans^=base[i];
			k>>=1;
		}
	}
	return ans;
}
signed main(){
	cin>>n>>l>>r;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=n;i++){
		insert(a[i]); 
	}
	rebuild();
	for(int i=l;i<=r;i++){
		cout<<query_k(i)<<' ';
	}
	return 0;
}

后记

终于把线性基的技能点点满啦！