【总结】重链剖分

好吧，现在让我来说一下树链剖分中的重链剖分。

Part one

首先让我来说一下什么是树链剖分。

实如其名，就是将一棵树化分成若干条连，下面是一个图。

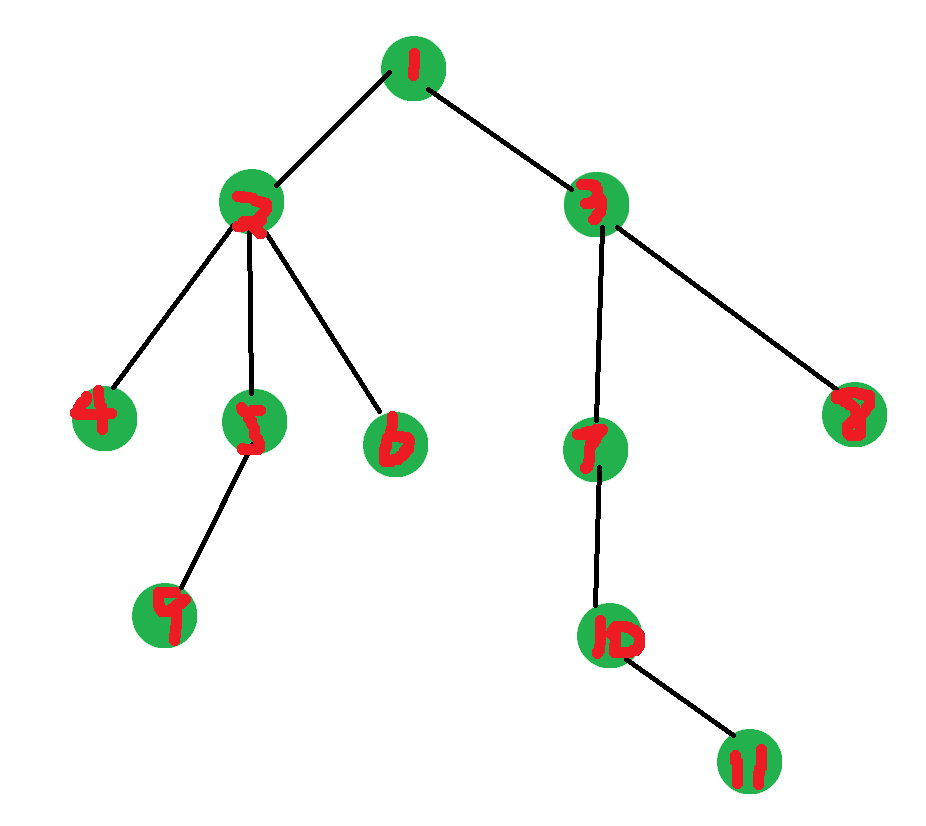
在这个图中你怎末划分都行。

下面是几种方案。

第 \(1\) 条链：\(1,2,4\)。

第 \(2\) 条链：\(5,9\)。

第 \(3\) 条连：\(6\)。

第 \(4\) 条链：\(3,8\)。

第 \(5\) 条链：\(7,10,11\)。

这就是一种划分的方式。

不过把数划分成若干条连有什莫好处呢。（没好处你学它干甚。

这可以方便你处理一些树上问题。（废话，不然还能处理序列上的问题吗。

Part two

你可能会问，怎末就 \(part2\) 了呢，上头都讲了写啥？

实际就是基本上啥也没讲。

别急，现在开始本文的重头戏。

树链剖分可以分成两类，一类叫作长链剖分，一类叫作重链剖分。

而长链剖分就是让每个点向它子孙中最深的点剖。

就像下图：

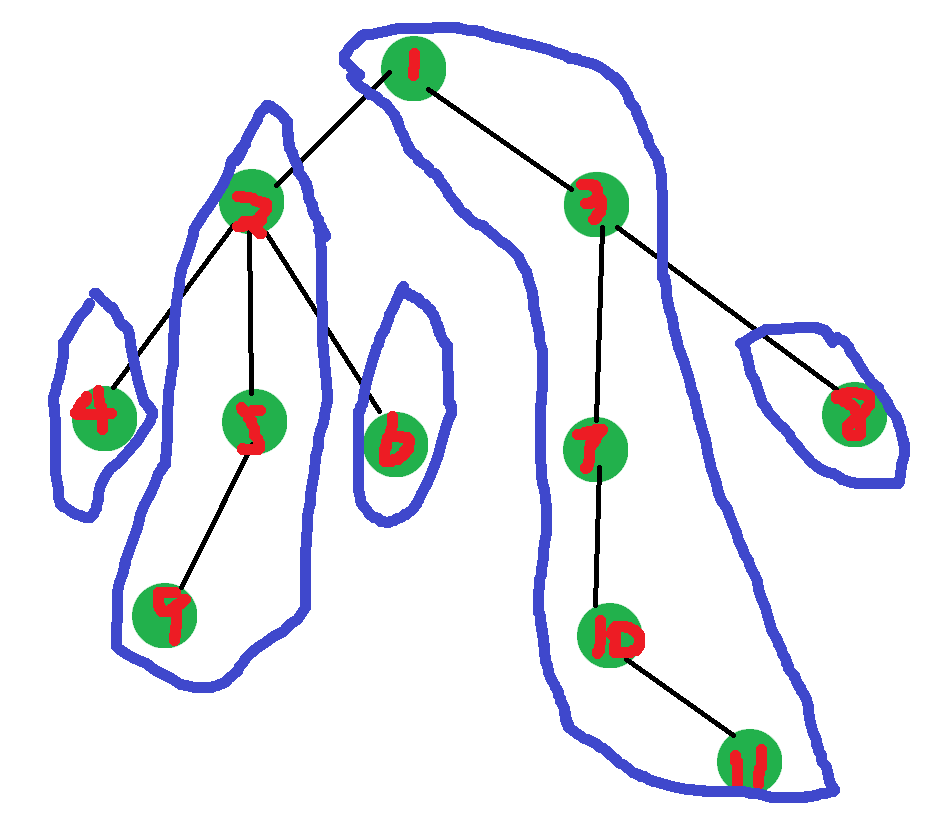
这个的用处主要在于 dp 优化啥的，今天先不讲。

下面是今天的主角——重链剖分。

重链剖分又是啥呢，就是每一个节点向它的儿子当中子孙最多的节点剖，就像这样：

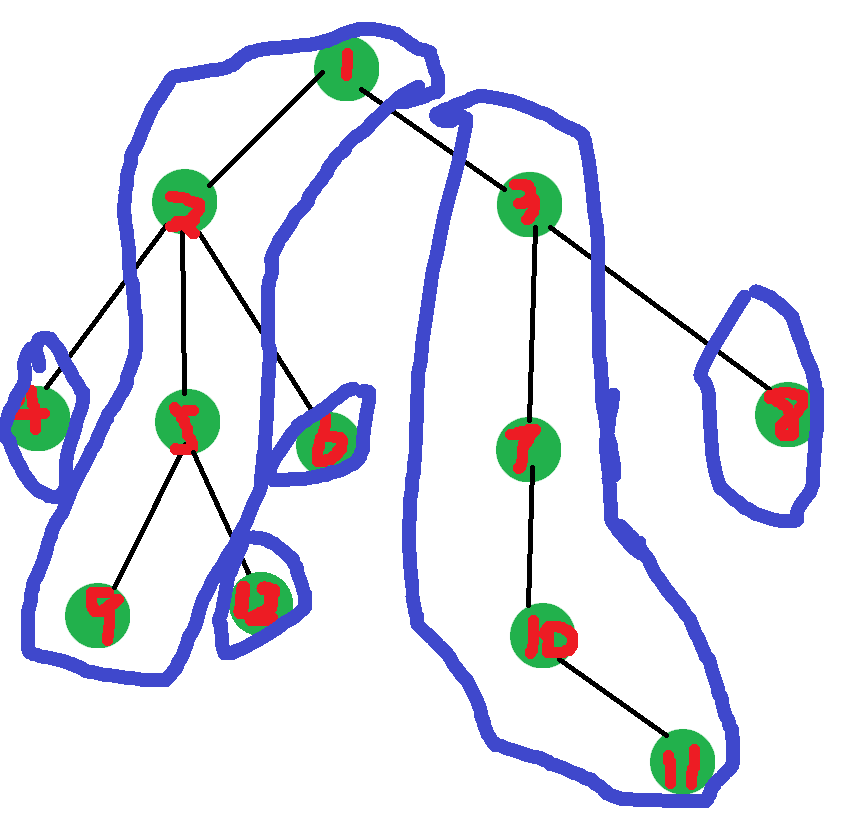
而重链剖分支干啥的呢。

它可以对树上进行区间操作，比如树上子树加，树上路经查询啥的。

虽然这里用区间很不准确，但一想到这个词，想必很多人会想到另一个名词：线段树。

线段树是干啥的，是用来维护序列上的区间操作。

所以就会有人想，能不能在树上建线段树。

于是重链剖分出现了。

那这和重链剖分有啥关系呢？

想一下，树为什么不能建线段树，因为树的各个节点很难组成一段连续的区间。

但是如果找到一个顺序，将树分成好几块，操作和查询的时候也是分成好几块，这样就会大大降低复杂度。

考虑 dfs 序，这个是比较容易被卡的，因为太不连贯了，所以排除。

接下来让我们谈谈按照重链头的 dfs 顺序排序的首尾相连的序列。

先想一下如何操作以 \(x\) 为根的子树。

首先一个树的根会先被 dfs 到，且在 dfs 完这颗子树前是不会到其他子树内的，所以到这颗子树的最后一个点只需加上这个子树大小再减 \(1\) 即可，这就是这棵子树映射到序列上的区间。

同时这也是 dfs 序所拥有的。

查询 \(x\) 到 \(y\) 的路径呢。

首先一个点要么在链中要么在链首（纯废话。

那么我们可以重链长驱直上，直至 \(x\) 和 \(y\) 到了同一个点即可。

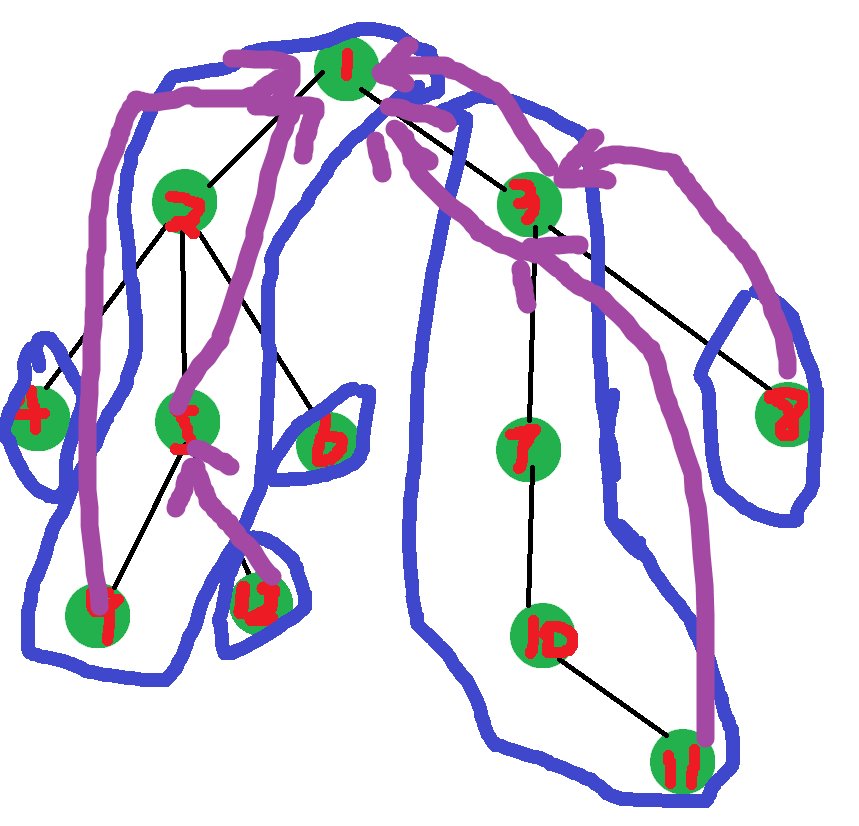
这是 \(9,13,11,8\) 这 \(4\) 个叶子节点到 \(1\) 节点的路径。

可见这是十分连贯的，所以说重链是可以实现树上路径修改的。

Part three

现在让我们对着例题详将一下代码。

Step one

先用一个 dfs 去处理一下一个结点的重儿子，父节点，子树大小，深度。

ll fa[N],siz[N],dep[N]/*deep(深度)*/;
ll hson[N];
void dfs1(ll x,ll fax){
	fa[x]=fax;
	siz[x]=1;
	dep[x]=dep[fax]+1;
	ll g=-1;
	for(ll i=0;i<e[x].size();i++){
		ll v=e[x][i];
		if(v==fax)continue;
		dfs1(v,x);
		siz[x]+=siz[v];
		if(g<siz[v]){
			g=siz[v];
			hson[x]=v;
		}
	}
} 

Step two

再用一个 dfs 去处理节点所属链头在映射序列中的位置，和该节点在序列上的位置。

注意这里应该先 dfs 重儿子，为啥，因为这是重链，重链上的点应该是连续的（虽然这样解释没有一点逻辑性，但至少对我来说是能让这个更好记）。

ll top[N];
ll tot=0;
ll dfn[N];
void dfs2(ll x,ll zt/*重(z)链top*/){
	top[x]=zt;
	dfn[x]=++tot;
	if(w[x]!=0)modify(1,1,n,dfn[x],dfn[x],w[x]); 
	if(hson[x]==0)return ;
	dfs2(hson[x],zt);
	for(ll i=0;i<e[x].size();i++){
		ll v=e[x][i];
		if(v==fa[x]||v==hson[x])continue;
		dfs2(v,v);
	}
}

Step three

查询和修改。

对子树的部分已经说过了。

void add_sontree(ll x,ll z){
	z%=mod;
	modify(1,1,n,dfn[x],dfn[x]+siz[x]-1,z);
}
ll query_sontree(ll x){
	return query(1,1,n,dfn[x],dfn[x]+siz[x]-1);	
}

对 \(x\) 到 \(y\) 路径部分。

就是像找 \(lca\) 一样向上跳，只不过 \(lca\) 是倍增，这里是跳重链。

什么时候不跳了呢，就是到他两个跳到了同一个重链的时候就不用跳了。

那在同一个重链上了点的编号就是连续的了，就直接搞就行了啊。

void add_path(ll l,ll r,ll k){
	k%=mod;
	while(top[l]!=top[r]){
		if(dep[top[l]]<dep[top[r]])swap(l,r);
		modify(1,1,n,dfn[top[l]],dfn[l],k);
		l=fa[top[l]];
	}
	if(dep[l]>dep[r])swap(l,r);
	modify(1,1,n,dfn[l],dfn[r],k);
}
ll query_path(ll l,ll r){
	ll cnt=0;
	while(top[l]!=top[r]){
		if(dep[top[l]]<dep[top[r]])swap(l,r);
		cnt=(cnt+query(1,1,n,dfn[top[l]],dfn[l]))%mod;
		l=fa[top[l]];
	}
	if(dep[l]>dep[r])swap(l,r);
	cnt=(cnt+query(1,1,n,dfn[l],dfn[r]))%mod;
	return cnt;	
}

Step four

#include<bits/stdc++.h>
using namespace std;
typedef int ll;
const ll N=1e5+5;
ll n,q,root,mod;
struct node{
	ll sum;
	ll lazy_tag; 
	ll l,r;
}tr[N*4];
void build(ll id,ll l,ll r){
	tr[id].l=l;
	tr[id].r=r;
	tr[id].lazy_tag=0;
	if(l==r){
		tr[id].sum=0;
		return ;
	}
	ll mid=(l+r)/2;
	build(id*2,l,mid);
	build(id*2+1,mid+1,r);
	tr[id].sum=tr[id*2].sum+tr[id*2+1].sum;
}
void pushdown(ll id){
	if(tr[id].lazy_tag!=0){
//		tr[id].lazy_tag%=mod;
		tr[id*2].lazy_tag+=tr[id].lazy_tag;
		tr[id*2].lazy_tag%=mod;
		tr[id*2+1].lazy_tag+=tr[id].lazy_tag;
		tr[id*2+1].lazy_tag%=mod;
		tr[id*2].sum=(tr[id*2].sum+((tr[id*2].r-tr[id*2].l+1)*tr[id].lazy_tag)%mod)%mod;
		tr[id*2+1].sum=(tr[id*2+1].sum+((tr[id*2+1].r-tr[id*2+1].l+1)*tr[id].lazy_tag)%mod)%mod;
		tr[id].lazy_tag=0;
	}
}
void modify(ll id,ll l,ll r,ll ql,ll qr,ll k){
	if(ql<=l&&r<=qr){
		tr[id].lazy_tag=(tr[id].lazy_tag+k)%mod;
		tr[id].sum=(tr[id].sum+(k*(r-l+1))%mod)%mod;
		return ;
	}
	pushdown(id);
	ll mid=(l+r)/2;
	if(ql<=mid)modify(id*2,l,mid,ql,qr,k);
	if(qr>mid)modify(id*2+1,mid+1,r,ql,qr,k);
	tr[id].sum=(tr[id*2].sum+tr[id*2+1].sum)%mod;
}
ll query(ll id,ll l,ll r,ll ql,ll qr){
	if(ql<=l&&r<=qr)return tr[id].sum;
	pushdown(id);
	ll mid=(l+r)/2;
	ll ans=0; 
	if(ql<=mid)ans=(ans+query(id*2,l,mid,ql,qr))%mod;
	if(qr>mid)ans=(ans+query(id*2+1,mid+1,r,ql,qr))%mod;
	return ans;
}
ll w[N];
vector<ll>e[N];
ll fa[N],siz[N],dep[N]/*deep(深度)*/;
ll hson[N];
void dfs1(ll x,ll fax){
	fa[x]=fax;
	siz[x]=1;
	dep[x]=dep[fax]+1;
	ll g=-1;
	for(ll i=0;i<e[x].size();i++){
		ll v=e[x][i];
		if(v==fax)continue;
		dfs1(v,x);
		siz[x]+=siz[v];
		if(g<siz[v]){
			g=siz[v];
			hson[x]=v;
		}
	}
} 
ll top[N];
ll tot=0;
ll dfn[N];
void dfs2(ll x,ll zt/*重(z)链top*/){
	top[x]=zt;
	dfn[x]=++tot;
	if(w[x]!=0)modify(1,1,n,dfn[x],dfn[x],w[x]); 
	if(hson[x]==0)return ;
	dfs2(hson[x],zt);
	for(ll i=0;i<e[x].size();i++){
		ll v=e[x][i];
		if(v==fa[x]||v==hson[x])continue;
		dfs2(v,v);
	}
}
void add_path(ll l,ll r,ll k){
	k%=mod;
	while(top[l]!=top[r]){
		if(dep[top[l]]<dep[top[r]])swap(l,r);
		modify(1,1,n,dfn[top[l]],dfn[l],k);
		l=fa[top[l]];
	}
	if(dep[l]>dep[r])swap(l,r);
	modify(1,1,n,dfn[l],dfn[r],k);
}
ll query_path(ll l,ll r){
	ll cnt=0;
	while(top[l]!=top[r]){
		if(dep[top[l]]<dep[top[r]])swap(l,r);
		cnt=(cnt+query(1,1,n,dfn[top[l]],dfn[l]))%mod;
		l=fa[top[l]];
	}
	if(dep[l]>dep[r])swap(l,r);
	cnt=(cnt+query(1,1,n,dfn[l],dfn[r]))%mod;
	return cnt;	
}
void add_sontree(ll x,ll z){
	z%=mod;
	modify(1,1,n,dfn[x],dfn[x]+siz[x]-1,z);
}
ll query_sontree(ll x){
	return query(1,1,n,dfn[x],dfn[x]+siz[x]-1);	
}
int main(){
	cin>>n>>q>>root>>mod;
	for(ll i=1;i<=n;i++)cin>>w[i];
	for(ll i=1;i<n;i++){
		ll u,v;
		cin>>u>>v;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	build(1,1,n);
	dfs1(root,0);
	dfs2(root,root);
	while(q--){
		ll op;
		cin>>op;
		if(op==1){
			ll l,r,k;
			cin>>l>>r>>k;
			add_path(l,r,k);
		}else if(op==2){
			ll l,r;
			cin>>l>>r;
			cout<<query_path(l,r)<<"\n";
		}else if(op==3){
			ll x,z;
			cin>>x>>z;
			add_sontree(x,z);
		}else{
			ll x;
			cin>>x;
			cout<<query_sontree(x)<<"\n";
		}
	}
	return 0;
}

打线段树一定要建树，不然。。。