【总结】指对幂函数

自从从 zr 回来，就感觉高中数学降了一个梯级。

指数函数

其实吧，指数函数没什么好说的，就是那么多。

有理数指数幂

整数指数幂

初中都学了。

分数指数幂

规定：$a^{\frac{m}{n}} = \sqrt[n]{a^{m}} $。

无理数指数幂

知道它仍然成立即可。

运算性质

\(1.a^{r}\cdot a^{s}=a^{r+s}\)

\(2.(a^{r})^{s}=a^{rs}\)

\(3.(ab)^{r}=a^{r}b^{r}\)

来一到自认为还不错的例题试试。

若方程 \(|3^{x}-1|=k\) 有一解，求 \(k\) 的取值范围。

画图题。

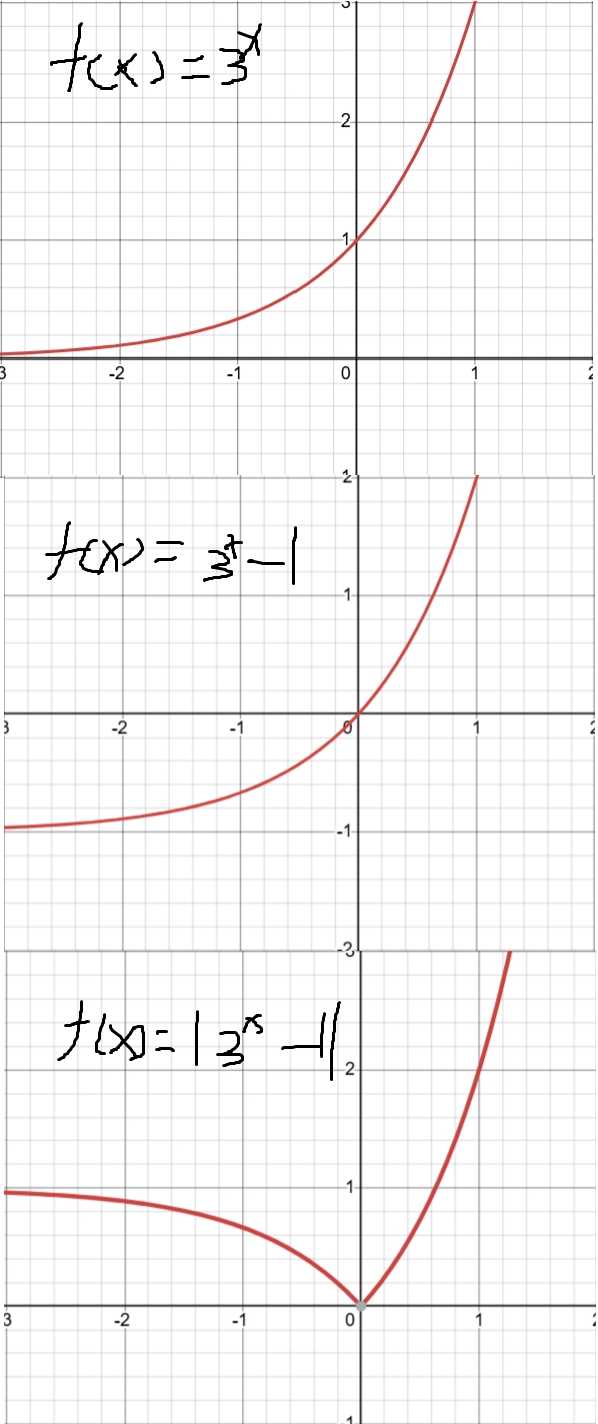
如图得，\(k\) 的取值范围是 \(k=0\) 或 \(k\ge 1\)。

对数函数

对数的基本性质

1. 当 \(a>0\) ，且 \(a\ne 1\) 时 $a^{x}=N\Leftrightarrow x=\log_{a}{N} $。

2. 当 \(N\le 0\) 时，\(N\) 没有对数。

特殊的对数函数

1. 以 \(10\) 为底的是 \(y=\lg{x}\)。

2. 以 \(e\) 为底的是 \(y=\ln{x}\)。

懒得讲了，来道信奥例题勇气。

不会看题解，我写过，自己搜。

幂函数

太简单了。