【题解】P4563 [JXOI2018] 守卫

思路

解法：区间 DP。

本题虽标上紫题，但黄队说了：“不要被颜色所吓倒。”

易得，区间 \([l,r]\) 中最右端的亭子 \(r\) 一定会有保镖。

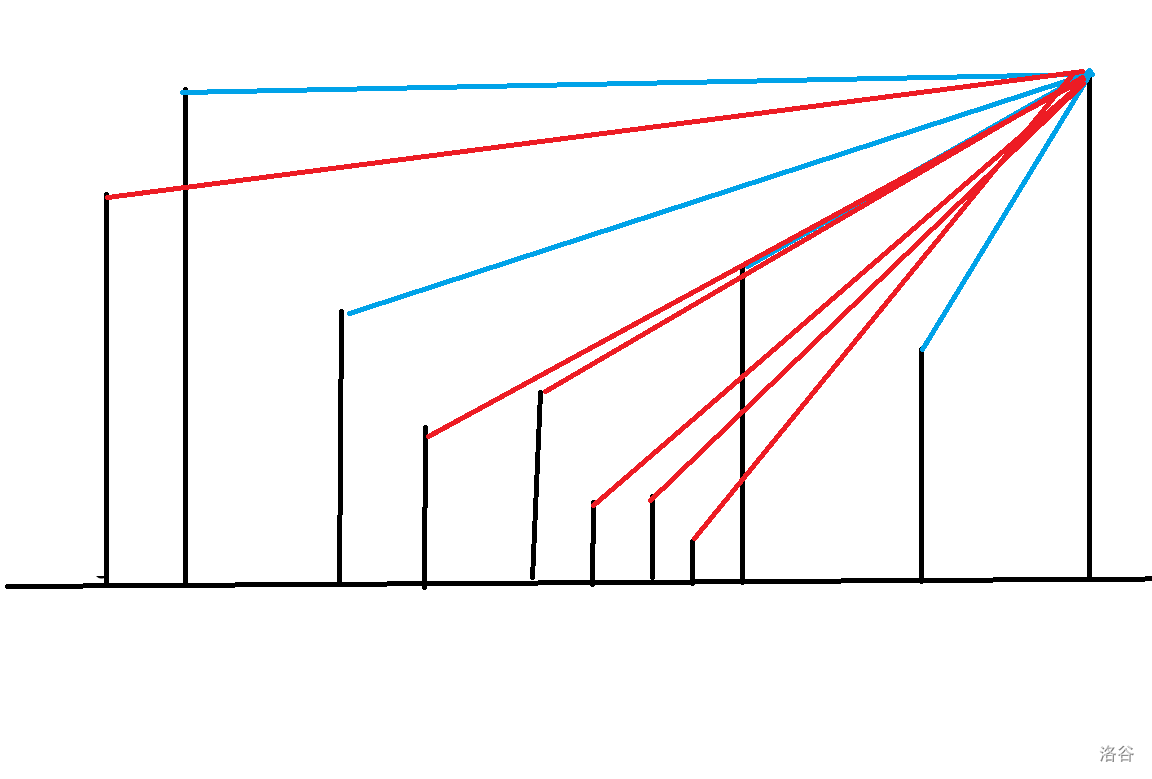
先说一下可见性判断吧，只要 \(l,r\) 的连线的斜率大于 \(p,r\) 连成的线的斜率大，\(l\) 即是可见的。

如图，红线是 \(r\) 无法看到的，而蓝线是 \(r\) 可以看到的，我们可以从 \(r\) 向 \(l\) 扫描，设 \(p\) 是 \(r\) 可以看到的最左端点，因次 \(p-1\) 必然低于 \(p\)。

则对于 \(l\) 到 \(p-1\) 一段，在 \(p\) 或 \(p-1\) 必有一个保镖。

易得 \(f_{l,r}=sum+\min(f_{l,p-1},f{l,p})\)。

若当前点 \(r\) 可见，则 \(p\) 和 \(p-1\) 中有一个保镖，则 \(sum\) 要加 \(\min(f_{l+1,p-1},f_{l+1,p}\)，将 \(p\) 更新成 \(l\)。

AC code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5010;
int f[N][N], h[N], n, ans = 0;
bool abledlook(int l, int x, int r) {
	return 1.0 * (h[x] - h[r]) / (x - r) > 1.0 * (h[r] - h[l]) / (r - l);//计算斜率
}
//判断是否可见

signed main() {
	cin >> n;

	for (int i = 1; i <= n; i++)cin >> h[i];
	for (int r = 1; r <= n; r++) {
		ans ^= (f[r][r] = 1);
		int sum = 1, p = 0;
		for (int l = r - 1; l >= 1; l--) {
			if (!p || abledlook(l, p, r))sum += min(f[l + 1][p - 1], f[l + 1][p]), p = l;//更新 p,sum

			ans ^= (f[l][r] = sum + min(f[l][p - 1], f[l][p]));
		}
	}

	cout << ans << "\n";
	return 0;
}