容斥与简单反演乱写
#define TBD ToBeDone 😅
容斥的本质
容斥原理首先基于这样的一个经验:求集合的交比求集合的并更简单,因此对于求并的问题,我们尝试向求交转化
容斥原理求解的是这样的问题:
有\(n\)个元素,每个元素可能有\(k\)种属性中的一种或多种
设\(A_i\)为至少含有属性\(i\)的元素构成的集合,若干个\(A_i\)的交是容易计算的
对于一个有\(s\)种属性的元素,我们希望其被统计\(g_s\)次,考虑每次在其\(s\)种属性中选出\(i\)种,在对应属性的\(i\)个集合\(A\)的并中统计一次。同时为了保证最后统计次数为\(g_s\),需要构造一个容斥系数\(f_i\),使得\(\sum\limits_{i=1}^s \binom{s}{i}f_i=g_s\)
对于\(g_s\)全部等于1的特殊情况,此时\(f_i = (-1) ^{(i - 1)}\),可以带入用二项式定理验证。
对于一般性的问题,由\(\sum\limits_{i=1}^{s+1} \binom{s+1}{i}f_i=g_{s+1}\)可以得到\(f_{s+1}=g_{s+1}-\sum\limits_{i=1}^s \binom{s+1}{i} f_i\),边界为\(f_0=0\),可以通过\(O(n^2)\)的递推或者\(O(n\log n)\)的多项式科技得到容斥系数。
例题
证明:对于\(n = \prod\limits_{i=1}^{k}{p_i ^ {c_i}}\) ,有\(\varphi(n) = n \times \prod\limits_{i=1}^{k}{\frac{p_i -1}{p_i}}\),其中\(p_i\)为\(n\)的质因子
为了统计小于\(n\)且与\(n\)互质的数,考虑对\(x\)的所有质因子进行容斥
在\([1, n]\)中,与\(n\)的\(\gcd\)为\(p_i\)的数有\(\lfloor\frac{n}{p_i} \rfloor\)个,与\(n\)的\(gcd\)为\(p_i\times p_j\)的数有\(\lfloor\frac{n}{p_i \times p_j} \rfloor\)个,以此类推
由容斥定理有,与\(n\)不互质的数有\(\sum\limits_{i}{\frac{n}{p_i}} - \sum\limits_{i < j}{\frac{n}{p_i\times p_j}} +...+(-1)^{k}\sum{\frac{n}{p_1 \times p_2 \times ... \times p_k}}\)
所以有\(\varphi(x) = n - \sum\limits_{i}{\frac{n}{p_i}} - \sum\limits_{i < j}{\frac{n}{p_i\times p_j}} +...+(-1)^{k}\sum{\frac{n}{p_1 \times p_2 \times ... \times p_k}}\)
上式等价于\(n \times \prod\limits_{i=1}^{k}(1 - \frac{1}{p_i})\)
sol
三个月前做过,现在不会了,不像某位神仙两年前做过现在一眼秒了😅比较navie的想法是设\(dp_{u,x}\)为\(u\)的子树中有\(x\)个点未被覆盖,需要子树外一个点向内某个点相连的方案数,直接类似树背包转移有 \(dp_{u,x + y - 2k} = \sum \limits_{v \in son(u), x +y > 0,k \leq min(x, y)} dp_{u, x} \times dp_{v,y} \times \binom{x}{k} \times \binom{y}{k} \times k!\)。
系数过于复杂,不便于优化。看到每条边至少被覆盖一次考虑容斥。
考虑边集\(S\)中的边一次都没被覆盖过,这等价于删去这些边。此时整张图被分成了若干个联通块,显然每个联通块内部匹配的方案数是 \(g(n) = \prod \limits _{2k \leq n, k \in N^*}{2k - 1}\),注意\(n\)为奇数时\(g(n) = 0\)。
数据范围无法枚举子集,考虑\(dp\),重定义\(dp_{u,x}\)为以\(u\)为根的子树联通块大小为\(x\)的方案数(考虑容斥系数)。那么有这条边断掉 \(dp_{u,x} \times dp_{v,y} \times{g(y)} \times -1 \rightarrow dp_{u,x}\) (断边集合大小加一),保留这条边 \(dp_{u,x} \times dp_{v,y} \rightarrow dp_{u, x +y}\)。
最后答案即为 \(\sum \limits_{i = 1} ^n dp_{1, i} \times g(i)\)。复杂度为树形背包的 \(O(n ^2)\)。
点击查看代码
#include <bits/stdc++.h>
void solve() {
int n;
std::cin >> n;
std::vector <std::vector<int> > adj(n + 1);
for (int i = 1; i < n; i++) {
int u, v;
std::cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
const int MOD = 1e9 + 7;
std::vector <int> g(n + 1);
g[0] = 1;
for (int i = 2; i <= n; i += 2) g[i] = 1ll * g[i - 2] * (i - 1) % MOD;
std::vector <std::vector<int> > dp(n + 1);
std::vector <int> siz(n + 1);
for (int i = 0; i <= n; i++) dp[i].resize(n + 1);
auto dfs = [&](auto self, int u, int fa) -> void {
siz[u] = 1;
dp[u][1] = 1;
for (const auto &v : adj[u]) {
if (v == fa) continue;
self(self, v, u);
std::vector <int> tmp(siz[u] + siz[v] + 1);
for (int j = 1; j <= siz[u]; j++) {
for (int k = 1; k <= siz[v]; k++) {
tmp[j] += -1ll * dp[u][j] * dp[v][k] % MOD * g[k] % MOD;
tmp[j] %= MOD; tmp[j] += MOD; tmp[j] %= MOD;
tmp[j + k] += 1ll * dp[u][j] * dp[v][k] % MOD;
tmp[j + k] %= MOD;
}
}
siz[u] += siz[v];
for (int i = 1; i <= siz[u]; i++) dp[u][i] = tmp[i];
}
};
dfs(dfs, 1, 0);
int ans = 0;
for (int i = 1; i <= n; i++) {
ans += 1ll * dp[1][i] * g[i] % MOD;
ans %= MOD;
}
std::cout << ans << "\n";
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int t = 1;
while (t--) {
solve();
}
return 0;
}
子集反演
若\(g(s) = \sum\limits_{t \subseteq s} f(t)\),那么有 \(f(s) = \sum \limits_{t \subseteq s} (-1) ^ {(|s| - |t|)}g(t)\)。(子集形式)
若\(g(s) = \sum\limits_{s \subseteq t} f(t)\),那么有 \(f(s) = \sum \limits_{s \subseteq t} (-1) ^ {(|t| - |s|)}g(t)\)。(超集形式)
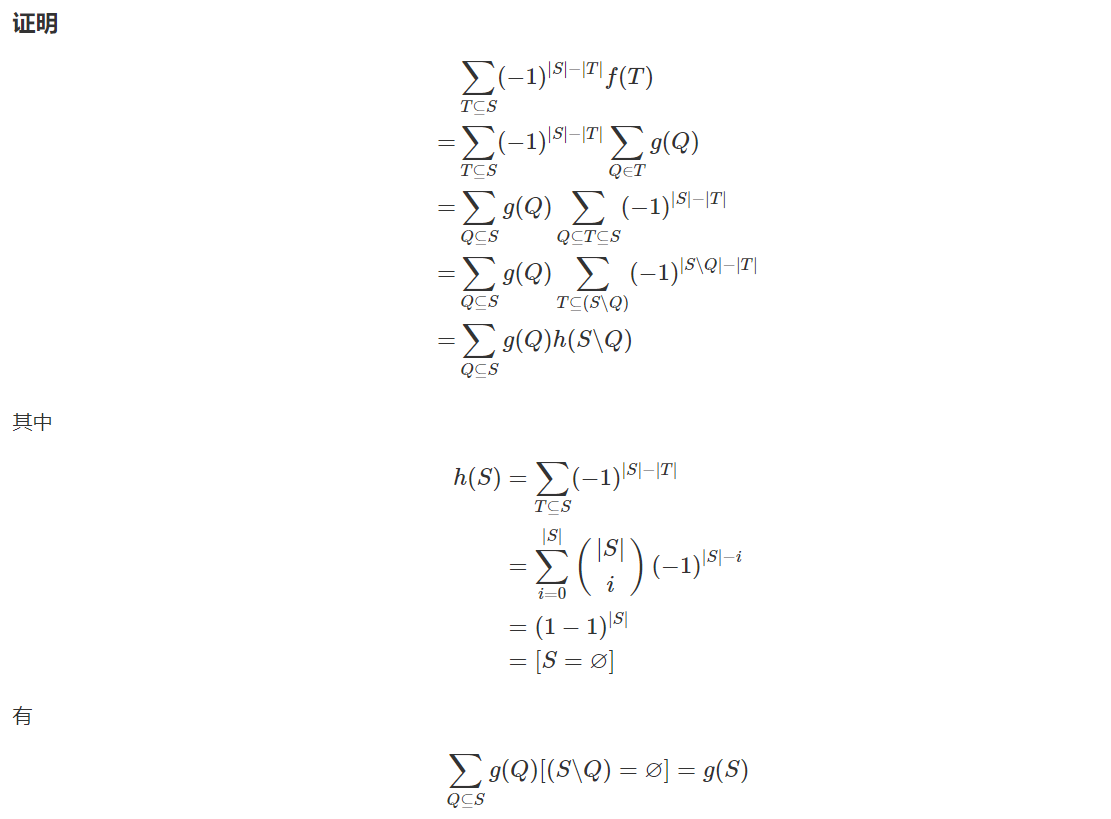
例题
TBD
二项式反演
若\(g_n = \sum\limits_{i = 0} ^ n \binom{n}{i} f_i\),那么有\(f_n = \sum\limits_{i = 0} ^ n (-1) ^ {(n - i)}\binom{n}{i} g_i\)。
若\(g_n = \sum\limits_{i = n} ^ m \binom{i}{n} f_i\),那么有\(f_n = \sum\limits_{i = n} ^ m (-1) ^ {(i - n)}\binom{i}{n} g_i\)。
证明:咕咕咕。
发现两种形式左右都是对称的,且-1的次数都为\(|i - n|\),便于背诵。
本质是容斥在大小相同的集合贡献相同的一种特殊形式。
一般设\(f_n\)为恰好取\(n\)个的值,\(g_n\)为钦定取\(n\)个的值,通常情况下后者比前者更好计算,就完成了从至少到恰好的转化
例题
sol:TBD
点击查看代码
#include <bits/stdc++.h>
void solve() {
int n, k;
std::cin >> n >> k;
const int MOD = 1e9 + 7;
std::vector <int> fac(n + 1), inv(n + 1);
auto power = [&](int a, int b) {
int ret = 1;
for (; b; b >>= 1) {
if (b & 1) ret = (1ll * ret * a) % MOD;
a = (1ll * a * a) % MOD;
}
return ret;
};
fac[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = (1ll * fac[i - 1] * i) % MOD;
inv[n] = power(fac[n], MOD - 2);
for (int i = n - 1; i >= 0; i--) {
inv[i] = 1ll * inv[i + 1] * (i + 1) % MOD;
}
auto C = [&](int n, int m) {
return 1ll * fac[n] * inv[n - m] % MOD * inv[m] % MOD;
};
auto g = [&](int i, int j) {
int lim1 = n * (i + j) - i * j, lim2 = n * n - lim1;
return 1ll * C(n, i) * C(n, j) % MOD * power(k - 1, lim1) % MOD * power(k, lim2) % MOD;
};
auto f = [&](int x, int y) {
int ret = 0;
for (int i = x; i <= n; i++) {
for (int j = y; j <= n; j++) {
int v = 1ll * C(i, x) * C(j, y) % MOD * g(i, j) % MOD;
if ((i + j - x - y) & 1) ret -= v, ret %= MOD, ret += MOD, ret %= MOD;
else ret += v, ret %= MOD;
}
}
return ret;
};
std::cout << f(0, 0) << "\n";
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int t = 1;
while (t--) {
solve();
}
return 0;
}
sol:TBD
点击查看代码
#include <bits/stdc++.h>
const int MAXN = 5005;
const int MOD = 998244353;
int dp[MAXN][MAXN];
void solve() {
int n, m;
std::cin >> n;
m = n / 2;
std::string s;
std::cin >> s;
std::vector <int> col(n + 1);
for (int i = 1; i <= n; i++) col[i] = s[i - 1] - '0';
std::vector <std::vector<int> > adj(n + 1);
for (int i = 1; i < n; i++) {
int u, v;
std::cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
auto power = [&](int a, int b) {
int ret = 1;
for (; b; b >>= 1) {
if (b & 1) ret = (1ll * a * ret) % MOD;
a = (1ll * a * a) % MOD;
}
return ret;
};
std::vector <int> fac(n + 1), inv(n + 1);
fac[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = (1ll * fac[i - 1] * i) % MOD;
inv[n] = power(fac[n], MOD - 2);
for (int i = n - 1; i >= 0; i--) {
inv[i] = (1ll * inv[i + 1] * (i + 1)) % MOD;
}
auto C = [&](int n, int m) {
return 1ll * fac[n] * inv[n - m] % MOD * inv[m] % MOD;
};
std::vector <std::vector<int> > siz(n + 1);
for (int i = 0; i <= n; i++) siz[i].resize(2);
auto dfs = [&](auto self, int u, int fa) -> void {
siz[u][col[u]] = 1; dp[u][0] = 1;
for (const auto &v : adj[u]) {
if (v == fa) continue;
self(self, v, u);
int s1 = (siz[u][0] + siz[u][1]) / 2, s2 = (siz[v][0] + siz[v][1]) / 2, s3 = (siz[u][0] + siz[u][1] + siz[v][0] + siz[v][1]) / 2;
std::vector <int> tmp(s3 + 1);
for (int j = 0; j <= s1; j++) {
for (int k = 0; k <= s2; k++) {
if (j + k > m) break;
tmp[j + k] += 1ll * dp[u][j] * dp[v][k] % MOD;
tmp[j + k] %= MOD;
}
}
siz[u][0] += siz[v][0], siz[u][1] += siz[v][1];
for (int i = 0; i <= s3; i++) dp[u][i] = tmp[i];
}
for (int i = siz[u][col[u] ^ 1]; i >= 0; i--) {
dp[u][i + 1] += 1ll * dp[u][i] * (siz[u][col[u] ^ 1] - i) % MOD;
dp[u][i + 1] %= MOD;
}
};
dfs(dfs, 1, 0);
auto g = [&](int x) {
return 1ll * dp[1][x] * fac[m - x] % MOD;
};
auto f = [&](int x) {
int res = 0;
for (int i = x; i <= m; i++) {
int v = 1ll * C(i, x) * g(i) % MOD;
if ((i - x) & 1) res -= v, res %= MOD, res += MOD, res %= MOD;
else res += v, res %= MOD;
}
return res;
};
for (int i = 0; i <= m; i++) {
std::cout << f(i) << "\n";
}
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int t = 1;
while (t--) {
solve();
}
return 0;
}
sol:TBD
点击查看代码
#include <bits/stdc++.h>
const int MAXN = 1005;
int dp[MAXN][MAXN][2][2];
void solve() {
int n, k;
std::cin >> n >> k;
#define ll long long
const int MOD = 1e9 + 7;
std::vector <int> fac(n + 1), inv(n + 1);
auto power = [&](int a, int b) {
int ret = 1;
for (; b; b >>= 1) {
if (b & 1) ret = (1ll * ret * a) % MOD;
a = (1ll * a * a) % MOD;
}
return ret;
};
fac[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = 1ll * fac[i - 1] * i % MOD;
inv[n] = power(fac[n], MOD - 2);
for (int i = n - 1; i >= 0; i--) {
inv[i] = 1ll * inv[i + 1] * (i + 1) % MOD;
}
auto C = [&](int n, int m) {
return 1ll * fac[n] * inv[m] % MOD * inv[n - m] % MOD;
};
dp[1][0][0][0] = dp[1][1][0][1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 0; j <= i; j++) {
//select i - 1
if (j) {
dp[i][j][0][0] += dp[i - 1][j - 1][0][0]; dp[i][j][0][0] %= MOD;
dp[i][j][1][0] += dp[i - 1][j - 1][0][1]; dp[i][j][1][0] %= MOD;
}
//select i + 1
if (j) {
dp[i][j][0][1] += dp[i - 1][j - 1][0][0]; dp[i][j][0][1] %= MOD;
dp[i][j][0][1] += dp[i - 1][j - 1][1][0]; dp[i][j][0][1] %= MOD;
dp[i][j][1][1] += dp[i - 1][j - 1][0][1]; dp[i][j][1][1] %= MOD;
dp[i][j][1][1] += dp[i - 1][j - 1][1][1]; dp[i][j][1][1] %= MOD;
}
//select nothing
dp[i][j][0][0] += dp[i - 1][j][1][0]; dp[i][j][0][0] %= MOD;
dp[i][j][0][0] += dp[i - 1][j][0][0]; dp[i][j][0][0] %= MOD;
dp[i][j][1][0] += dp[i - 1][j][0][1]; dp[i][j][1][0] %= MOD;
dp[i][j][1][0] += dp[i - 1][j][1][1]; dp[i][j][1][0] %= MOD;
}
}
auto g = [&](int x) {
return 1ll * ((dp[n][x][1][0] + dp[n][x][0][0]) % MOD) * fac[n - x] % MOD;
};
auto f = [&](int x) {
int ret = 0;
for (int i = x; i <= n; i++) {
int v = 1ll * g(i) * C(i, x) % MOD;
if ((i - x) & 1) ret -= v, ret %= MOD, ret += MOD, ret %= MOD;
else ret += v, ret %= MOD;
}
return ret;
};
std::cout << f(k) << "\n";
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int t = 1;
while (t--) {
solve();
}
return 0;
}
Timber
sol:TBD
点击查看代码
#include <bits/stdc++.h>
void solve() {
int n, m, k;
std::cin >> n >> m >> k;
const int MOD = 998244353;
std::vector <int> fac(n + 1), inv(n + 1), pw(n + 1);
auto power = [&](int a, int b) {
int ret = 1;
for (; b; b >>= 1) {
if (b & 1) ret = (1ll * ret * a) % MOD;
a = (1ll * a * a) % MOD;
}
return ret;
};
fac[0] = 1; pw[0] = 1;
for (int i = 1; i <= n; i++) {
fac[i] = 1ll * fac[i - 1] * i % MOD;
pw[i] = 1ll * pw[i - 1] * 2 % MOD;
}
inv[n] = power(fac[n], MOD - 2);
for (int i = n - 1; i >= 0; i--) inv[i] = 1ll * inv[i + 1] * (i + 1) % MOD;
auto C = [&](int n, int m) {
if (n < 0 || m < 0) return 0ll;
if (m > n) return 0ll;
return 1ll * fac[n] * inv[n - m] % MOD * inv[m] % MOD;
};
#define ll long long
int ans = 0;
for (int i = 0; i <= m; i++) {
ll tmp = (ll)n - 1ll * (m + i) * k;
if (tmp < 0) continue;
int v = 1ll * pw[m - i] * C(m, i) % MOD * C(n - (m + i) * k, m) % MOD;
if (i & 1) ans -= v, ans %= MOD, ans += MOD, ans %= MOD;
else ans += v, ans %= MOD;
}
std::cout << ans << "\n";
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int t = 1;
while (t--) {
solve();
}
return 0;
}
广义容斥(容斥系数)
本人认为二项式反演不等于广义容斥,相反,只是容斥中的一种可以简化的特殊情况,只是容斥系数的推导可以用到二项式反演。
\( \begin{aligned} & \sum\limits_{i = 0} ^ {h_x} \binom {h_x}{i} f_i = g_x \\ & f_x = \sum\limits_{i = 0}^{h_x} (-1) ^ {(h_x - i)}\binom{h_x}{i} g_i \end{aligned} \)
例题
sol
设一个三角形由 \(t\) 个给定的三角形覆盖,那么有 \(f_t = \sum\limits_{i = 0} ^ {t} (-1) ^ {(t - i)} \binom{t}{i} [2 \nmid t]\)。
发现只有为\(i\)奇数时才有贡献,所以 \(f_t = (-1) ^ {(t - 1)}\sum\limits_{i = 0} ^ {t} \binom{t}{i} [2 \nmid t]\)。
考虑用二项式定理相减化简,具体来说如下。
\((a + b) ^ n - (a - b) ^ n = \sum\limits_{i = 0} ^ {n} \binom{n}{i} a ^ {n - i}b^i - \sum\limits_{i = 0} ^ {n} (-1) ^ i \binom{n}{i}a^{n - i}b^i = 2 \times \sum\limits_{i = 0} ^ n [2 \nmid n]\binom{n}{i}a^{n - i}b^i\)
所以有 \(f_t = (-1) ^ {(t - 1)} \frac{(1 + 1) ^ t - (1 - 1) ^ t}{2} = (-2) ^ {(t - 1)}\)。
然后枚举子集计算子集中三角形面积交乘上系数相加即可。
还有由于是等腰直角三角形,比较特殊,无需计算几何,初中知识即可。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
struct Tri {
int x, y, r;
double size() {
if (r < 0) return 0.0;
return 1.0 * r * r / 2.0;
}
Tri(int X = 0, int Y = 0, int R = 0) {
x = X; y = Y; r = R;
}
bool operator == (const Tri &t) const {
return x == t.x && y == t.y && r == t.r;
};
};
Tri merge(Tri x, Tri y) {
int c1 = x.x + x.y + x.r, c2 = y.x + y.y + y.r;
int mxx = std::max(x.x, y.x), mxy = std::max(x.y, y.y);
return Tri(mxx, mxy, std::min(c1, c2) - mxx - mxy);
}
void solve() {
int n;
std::cin >> n;
std::vector <Tri> a(n);
for (int i = 0; i < n; i++) {
std::cin >> a[i].x >> a[i].y >> a[i].r;
}
std::vector <int> f(n + 1);
f[1] = 1;
for (int i = 2; i <= n; i++) {
f[i] = -2 * f[i - 1];
}
double ans = 0;
for (int mask = 1; mask < (1 << n); mask++) {
int sz = __builtin_popcount(mask);
Tri tr = Tri(0, 0 ,0);
for (int i = 0; i < n; i++) {
if (mask & (1 << i)) {
if (tr == Tri(0, 0, 0)) tr = a[i];
else tr = merge(tr, a[i]);
}
}
double s = tr.size();
if (s) {
ans += 1.0 * f[sz] * s;
}
}
std::cout << std::fixed << std::setprecision(1) << ans << "\n";
// printf("%.1lf\n", ans);
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
int t = 1;
while (t--) {
solve();
}
return 0;
}
sol
没必要写了,如果写一遍多半会和别人的题解大幅度相似
点击查看代码
#include <bits/stdc++.h>
const int MAXN = 3005;
const int MOD = 998244353;
#define ll long long
int C[MAXN][MAXN], f1[MAXN], f2[MAXN], pw[MAXN * MAXN];
void Mod(int &x) {
if (x >= MOD) x -= MOD;
if (x < 0) x += MOD;
}
void Mod(ll &x) {
if (x >= MOD) x -= MOD;
if (x < 0) x += MOD;
}
void init() {
for (int i = 0; i < MAXN; i++) {
for (int j = 0; j <= i; j++) {
if (!j) C[i][j] = 1;
else C[i][j] = C[i - 1][j] + C[i - 1][j - 1], Mod(C[i][j]);
}
}
pw[0] = 1;
for (int i = 1; i < MAXN * MAXN; i++) pw[i] = pw[i - 1] + pw[i - 1], Mod(pw[i]);
}
void solve(int n, int m, int a, int b) {
int t = std::max(n, m);
for (int i = 0; i <= t; i++) {
f1[i] = f2[i] = 0;
}
f1[a] = f2[b] = 1;
for (int i = a + 1; i <= n; i++) {
for (int j = a; j < i; j++) {
f1[i] -= 1ll * C[i - 1][j - 1] * f1[j] % MOD;
Mod(f1[i]);
}
}
for (int i = b + 1; i <= m; i++) {
for (int j = b; j < i; j++) {
f2[i] -= 1ll * C[i - 1][j - 1] * f2[j] % MOD;
Mod(f2[i]);
}
}
ll ans = 0;
for (int i = a; i <= n; i++) {
for (int j = b; j <= m; j++) {
ans += 1ll * f1[i] * f2[j] % MOD * C[n][i] % MOD * C[m][j] % MOD * pw[(n - i) * (m - j)] % MOD;
Mod(ans);
}
}
std::cout << ans << "\n";
}
int main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
std::cout.tie(0);
init();
int n, m, a, b;
while (std::cin >> n >> m >> a >> b) {
solve(n, m, a, b);
}
return 0;
}
HDU5072 Coprime
TBD
莫比乌斯反演
link,这玩意儿严格来讲属于数论了,不在此展开。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号