解题报告——论对“数据分治”的新理解

解题报告——论对“数据分治”的新理解

所谓数据分治，就是对于一道题我们有多种算法，如果一个一个地运用这几种算法，每个都不能通过这道题，但是每种算法都有其最适合的数据范围，我们根据不同的数据运用不同的算法，就可以通过这道题。

一般的数据分治都是根据输入数据的规模分治的，但是有些数据分治是“思维上的”数据分治，跟输入数据完全无关，这样的数据分治，本身就可以是为一种算法，所以这样的题一般都是思维好题。

这道题告诉我们就算是 \(\text{OI}\) 的思维也可以运用到 \(\text{ACM}\) 赛制中。

先考虑一个最朴素的暴力，如果我们把 \(b\) 从 \(1\) 到 \(n\) 枚举，时间复杂度是 \(n\lg n\) 的，无法通过这道题。

再从反向思维考虑，我们枚举 \(n\) 最后变成了什么样，就是 \(n\) 在 \(b\) 进制下的 \(01\) 串长什么样，然后二分查找这个 \(b\) 是否存在，时间复杂度也是 \(n\log n\) 的。

现在想，如果我们已经确定了一个 \(b\)，那么 \(b\) 越大，上面那个算法的复杂度就越大，但是下面这个算法的 \(01\) 串就越短。

从这里开始我们就可以对 \(b\) 数据分治了。我设置的边界是 \(b\) 从 \(1\) 枚举到 \(3.5\times 10^4\)，\(01\) 串从 \(0001\) 枚举到 \(1111\)。

那么这道题目已经不重要了。我们剖析一下数据分治的本质。

回到一开头的定义来——通过这道题我们可以看到，有一些算法的复杂度随着 \(n\) 的增大而增大，但还有另外一些算法的复杂度随着 \(n\) 的增大而减小。如果我们把这些算法时间复杂度随 \(n\) 变化的关系画到一个函数图像上，那么其就像这样：

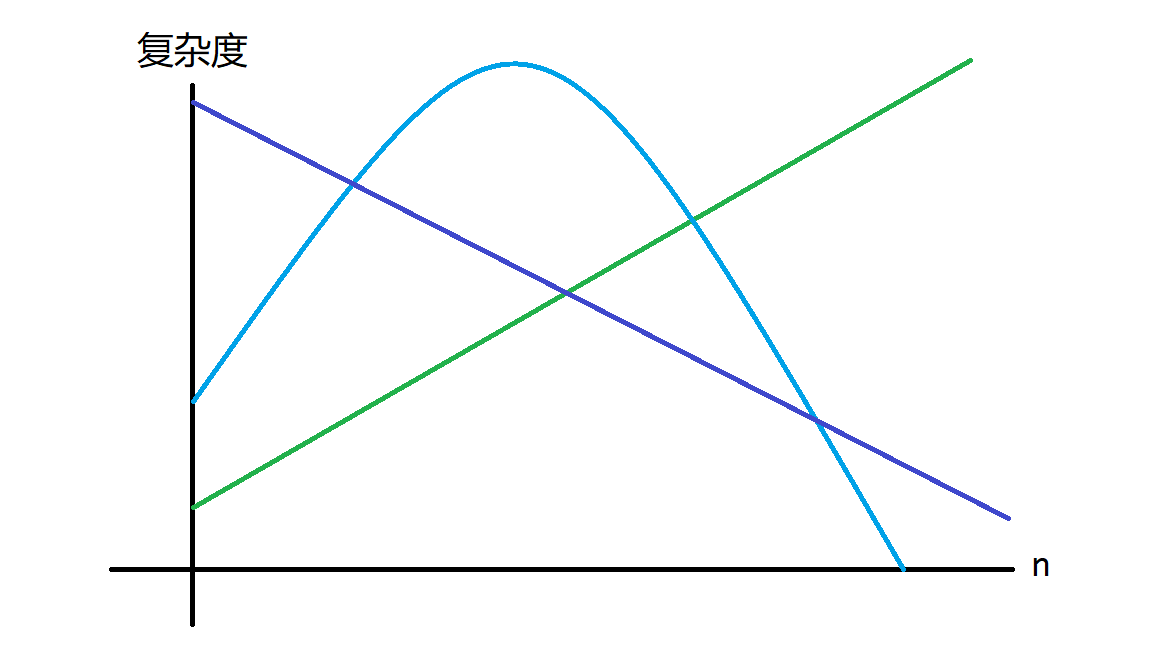
那么我们数据分治要干的是什么？对于每个 \(n\) 取到复杂度的最小值。那不就是凸包吗？

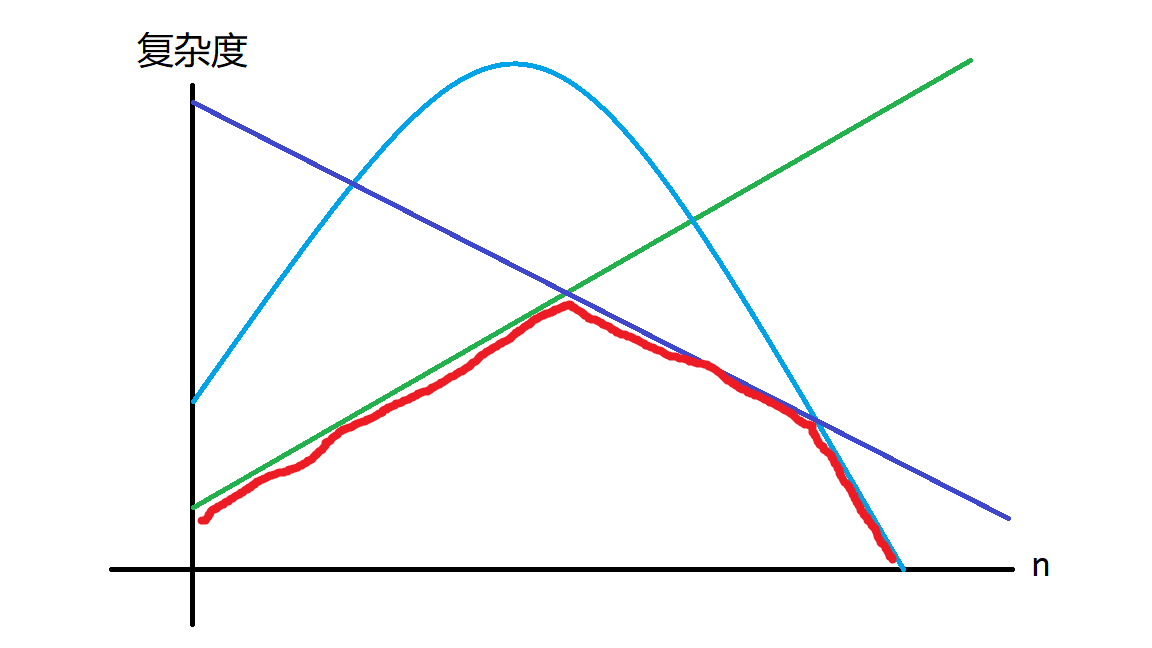
这启示我们：当我们想要数据分治但情况太复杂的时候，我们甚至可以搞个凸包来帮我们判断哪个数据用哪个算法，甚至还可以把这个凸包加到代码中。