面试可能遇到的关联式容器(map、set等)相关问题
>>>. map与set的区别是什么,各有哪些优势?
map中存储的数据是以键值对(key - value)形式并且通过排序(比较key,默认以 '<' 方式排序)存在的(每个key只能出现一次),set中存储的数据是以值单独通过排序(默认以 '<' 方式排序)存储(每个值只能出现一次), 对map和set容器进行迭代时都可以获得一个有序序列
>对于map来说,由于是关联容器,所以提供一对一的数据处理,而且可以使用 [ ](下标访问符),在 [ ] 中放入key,就可以得到key对应的value
>而对于set来说,可以通过自身值唯一性质来做数据的‘去重’操作
>注意:
map/multimap存储的是真正的键值对,set只存放value,但是set底层实际存放的是由value-value组成的键值对。
set中不允许修改元素(一般都为const类型),只能进行插入或者删除,map中也不允许修改key值,但是可以修改key对应的value
map与set查找效率都为O(log2N),底层实现都为红黑树
>>>. 红黑树是如何插入,如何旋转的。
红黑树也就是二叉搜索树,所以插入首先按照二叉搜索树方式插入,插入后观察各节点颜色是否满足红黑树性质(即根为黑,父母红则双子节点黑,叶子结点黑(包括空结点),每个结点到叶子结点简单路径上的黑结点数相同,以上4点)
所以插入后会出现以下几种情况:(cur为当前插入的结点)
>1.cur的父母结点(p)及其兄弟节点(u)为红,祖父节点(g)为黑
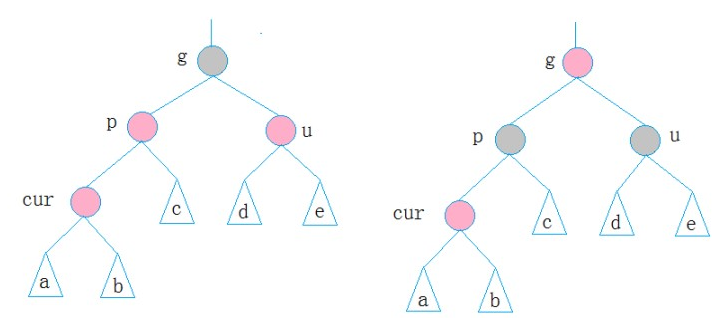
此时解决方法如图,将p,u 置为黑,将g置为红,之后继续向上调整(g看做cur继续调整)
>2.p为红,g为黑
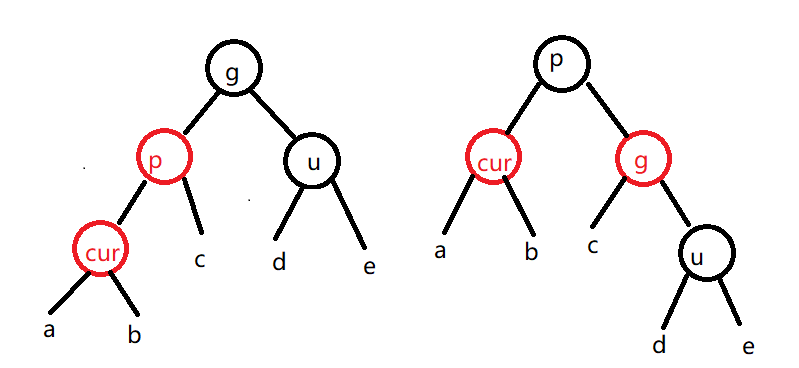
此时需要分情况进行:
若是p为g的左孩子,cur为p的左孩子,则进行右单旋转,然后p置为黑,g置为红(图示)。
若是p为g的右孩子,cur为p的右孩子(前一种对称翻转),则进行左单旋转,然后p置为黑,g置为红.
>3.p为红,g与u为黑(或者无u)

p为g的左孩子,cur为p的右孩子,则针对p做左单旋转
p为g的右孩子,cur为p的左孩子(前一种对称翻转),则针对p做右单旋转
则都可以转换为情况2,再根据情况2进行调整
>>>. map的迭代器会失效吗,什么情况下失效,如何处理。
与vector迭代器失效的场景相似,map的迭代器也会失效,如以下代码:
for (iter = dataMap.begin(); iter != dataMap.end();iter++){
int nKey = iter->first;
string strValue = iter->second;
if (nKey % 2 == 0){
dataMap.erase(iter);
//此时iter已经失效了,进入下一次循环++时就会报错
}
}
//这里有一个常见误区,就是map与vector的erase操作返回值是不同的
//vector中erase执行结束会返回删除元素的下一个元素的迭代器。如下
vector<int> v={1,2,3,4,5};
auto it=v.begin();
for(;it!=v.end();){
if(*it%2){
it=v.erase(it); //这一句执行完后it指向的是4,erase会自动移位
}
else it++;
}
//但是map中的erase不会自动移位,所以为了防止迭代器失效,通常使用以下两种方法编写:
//1
map<int,string> m;for (auto it = m.begin(); it != m.end();){
if (it->first % 2){
auto it1=it;
it++;
m.erase(it1);
}
else
it++;
}
//2
……
for (auto it = m.begin(); it != m.end();){
if (it->first % 2){
m.erase(it++); //使用++进行移位,此时it不会失效,因为++运算返回的是运算前的值
}
else
it++;
}
>>>. AVL数和红黑树相比,为什么map和set使用了红黑树,红黑树的优势是什么?
首先,AVL数和红黑树都是高效的二叉搜索树。红黑树并没有追求绝对的*衡,它只要求部分达到*衡,但是提出了为节点增加颜色,红黑是用非严格的*衡来换取增删节点时候旋转次数的降低,任何不*衡都会在三次旋转之内解决,而AVL有着*衡因子大于等于-1小于等于1的设定,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多。
虽然红黑树的查询性能略微逊色于AVL树(毕竟趋*绝对*衡),但是红黑树在插入和删除上优于AVL树,AVL树每次插入删除会进行大量的*衡度计算,而红黑树为了维持红黑性质所做的红黑变换和旋转的开销,相较于AVL树为了维持*衡的开销要小得多。
所以若搜索的次数远远大于插入和删除,那么选择AVL,如果搜索,插入删除次数几乎差不多,应该选择红黑树。也是出于这种综合性能的考虑,所以实际运用中红黑树更多
最后祝各位生活愉快~~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号