平衡树Splay与FHQ

树剖的未来会补的（卑微）。

这里想讲讲平衡树，因为看着高级，可以证明我学过OI。

我们先了解下 \(BST\)，也就是平衡二叉树。

他的概念是，对于每一个非叶子结点，他的左儿子一定小于当前节点，右儿子必定大于当前节点。

类似于如下图，就是一个好看的 \(BST\)：

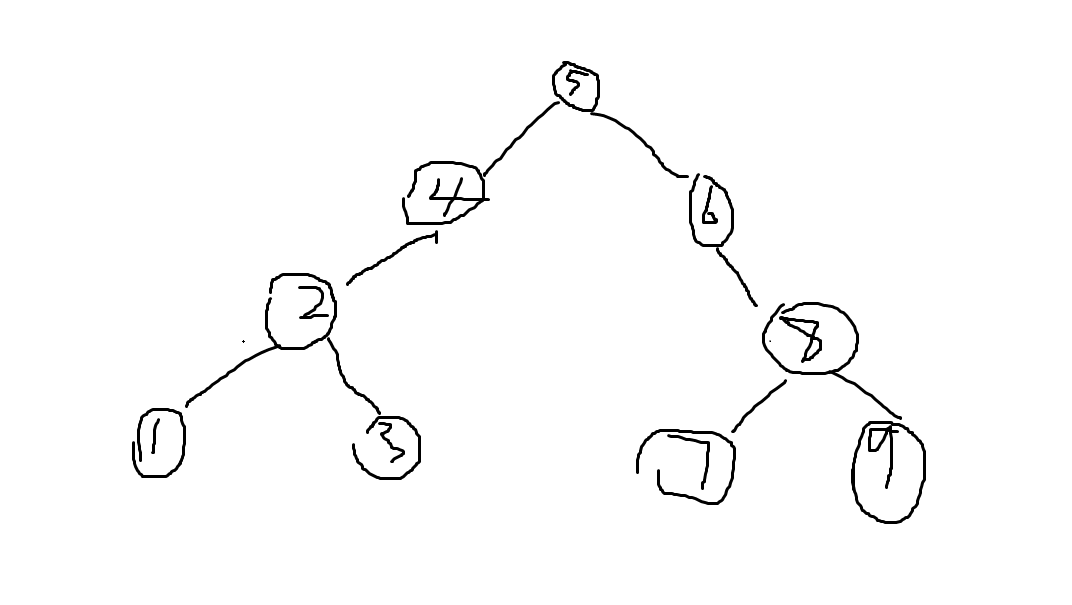
那我们现在对平衡二叉树有了深入的了解了，我们就开始进行平衡树的讲解。

一：平衡树解决的问题类型：

1.插入（删除）一个数

2.查询某个数的排名

3.查询某个排名所对应的数

4.查询某个数的前驱（后驱）

二：Splay

1.rotate 操作

分为左旋和右旋，我们偷一张图看一下：

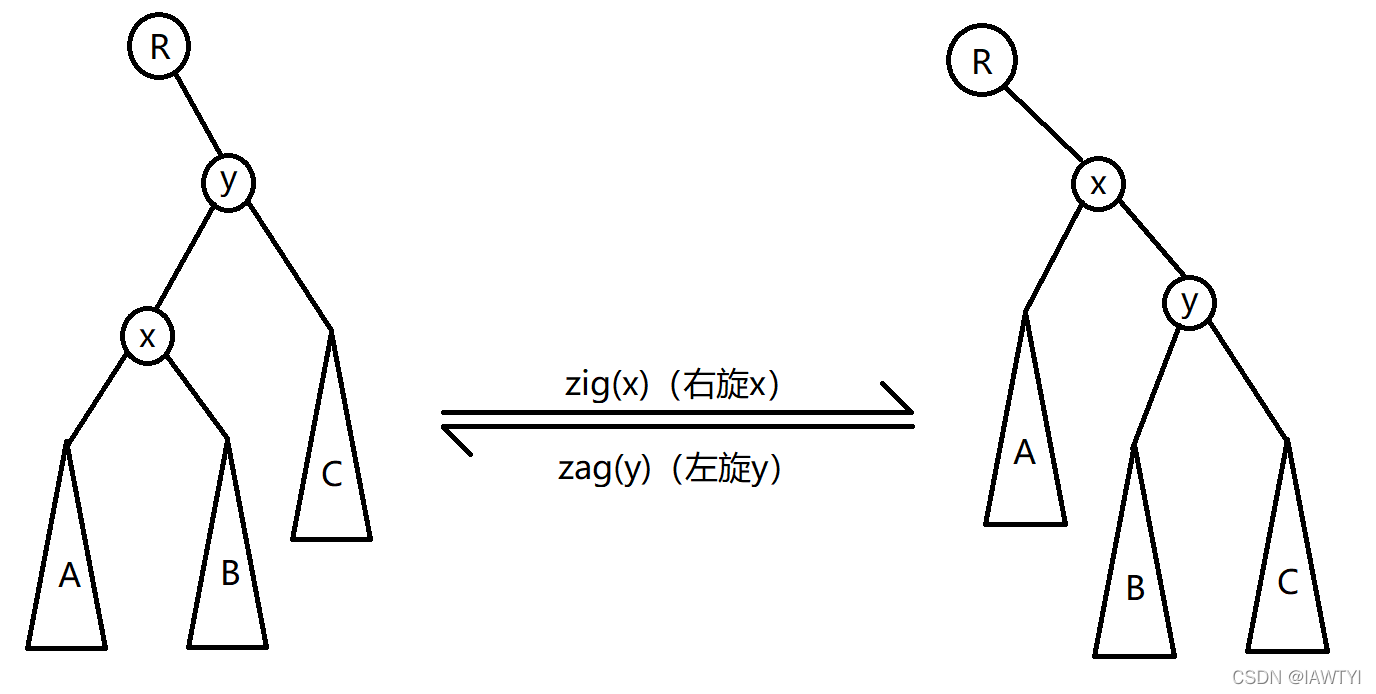
我们将 x 右旋，就是将 x 的父亲 (y) 变成 x 的右儿子，x 的右儿子变成 y 的左儿子，x 变为 R 的右儿子。

我们将 y 左旋，得到的结果和上面一样。

那么我们可以轻松写出 rotate 函数了：

inline void rotate(int x) {
	int idx = check(x);//x作为y的哪个儿子
		int f = tree[x].f, idf = check(f);//y和y作为R的哪个儿子
		int sonx = tree[x].son[idx ^ 1];//x的儿子（与x作为的儿子反着）
		int ff = tree[f].f;//y的父亲
		
		connect(sonx, f, idx);//将x的儿子变成y的儿子
		connect(f, x, idx ^ 1);//将x的父亲变成x的儿子
		connect(x, ff, idf);//将x变为原来y的父亲的对应儿子
		
		update(f);
		update(x);//修改当前节点子树的大小
}

2.splay 函数

Splay 的核心，不然也不配命名为 splay。

主要就是进行旋转，将 u 转到 v 的上。

那么我们分三种情况：

1.v 是 u 的父亲，如下图：

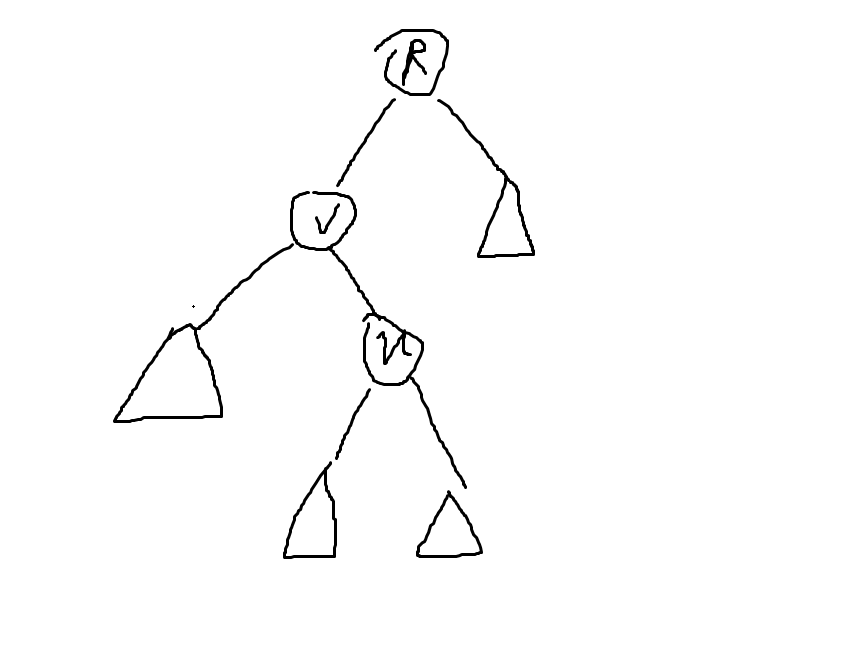
我们只需要将 u 转一下即可：

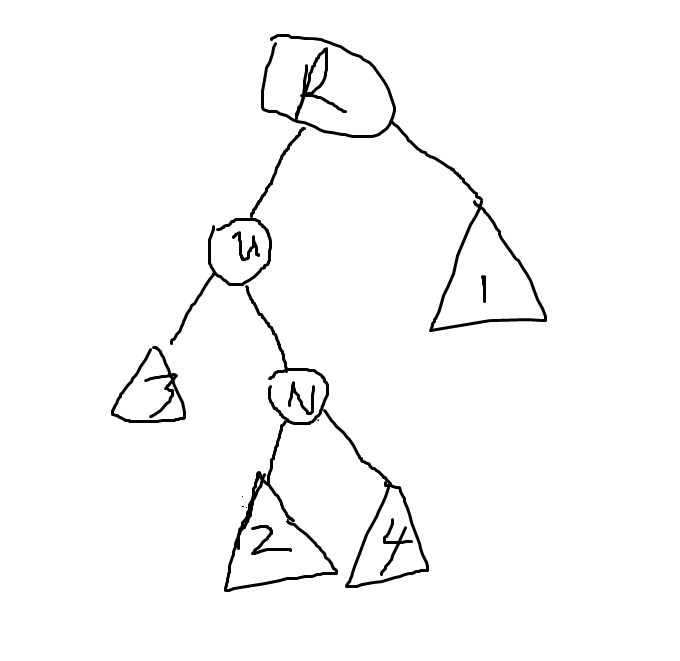
2.u 作为 u 的父亲 k 的左（右）儿子， k 也作为 k 的父亲 v 的左（右）儿子，如下图:

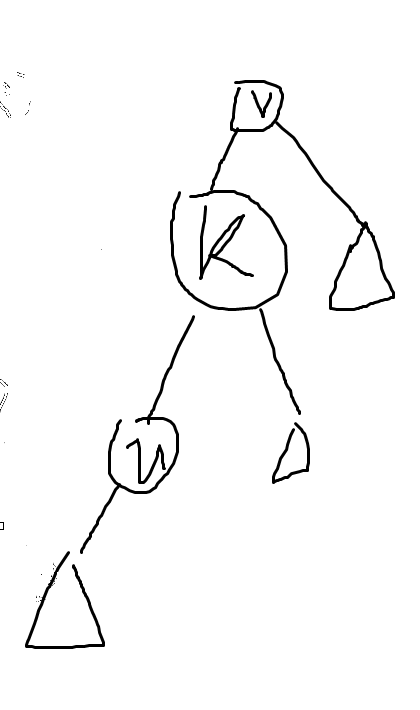
我们需要先旋转 k，再旋转 u：

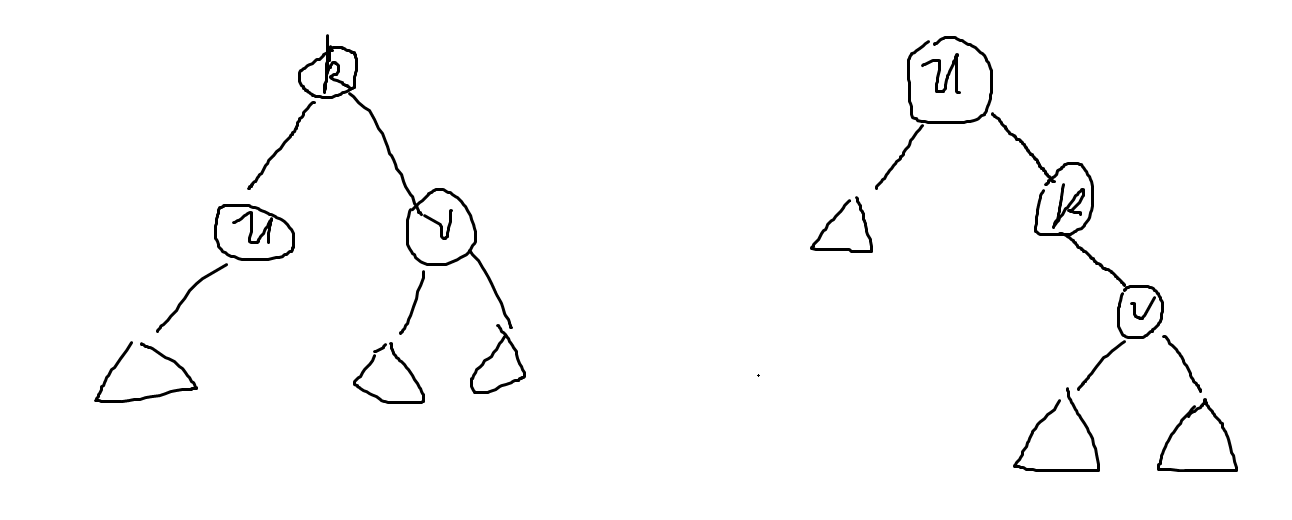
3.u 作为 u 的父亲 k 的左（右）儿子， k 也作为 k 的父亲 v 的右（左）儿子，如下图：

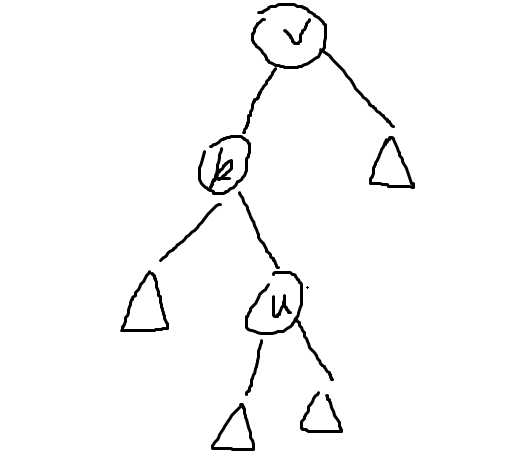
我们需要连选 2 次 u：

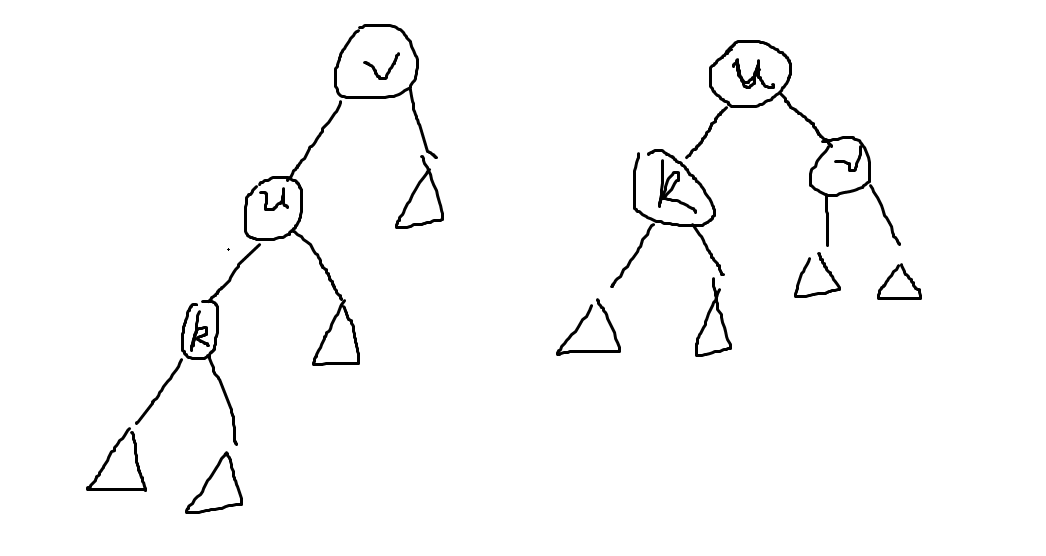
那么这样，我们可以很容易得到 splay 函数的代码：

inline void splay(int u, int v) {
	int fv = tree[v].f;
		
	while (fv != tree[u].f) {
		int fu = tree[u].f;
			
		if (fv == tree[fu].f) rotate(u);//v的父亲是u的父亲的父亲，即v是u的父亲		
		else if (check(u) == check(fu)) rotate(fu), rotate(u);//u和u的父亲分别同属于他们父亲的同种儿子
		else rotate(u), rotate(u);//与上面相反
	}
}

3.处理操作

1.插入：

那么是很显然的，只需要判断是否是相同的数即可。

相同的数，直接在频率上加一即可，否则建立新节点。

代码如下：

inline int add(int x, int fa) {
	tree[++ siz].data = x;
	tree[siz].f = fa;
	tree[siz].cnt = tree[siz].sum = 1;

	return siz;
}//添加一个节点

void push(int x) {
	int sign = 0, nxt;

	tot ++;

	if (! root) root = add(x, 0);//总得先有根节点吧……
	else {
		int now = root;

		while (now) {
			tree[now].sum ++;

			if (tree[now].data == x) {
				tree[now].cnt ++, sign = now;

				break; 
			} //已经有过这个数字，就将cnt++，位置标记

			nxt = tree[now].data < x ? 1 : 0;

			if (! tree[now].son[nxt]) {
				sign = tree[now].son[nxt] = add(x, now);

				break;
			}//这个节点还没有数字，就将这个数字差到当前节点

			now = tree[now].son[nxt];
		}
	}

	splay(sign, root);
}

2.删除：

这个操作复杂一点，可能不是很好理解。

我们要删除某个节点，肯定是要找到这个节点的吧。

所以必然会有查找的函数，这个函数也很简单，模拟即可：

inline int findd(int x) {
	int now = root, nxt;
		
	while (now) {
		if (tree[now].data == x) {
			splay(now, root);
				
			return now;
		}//找到了元素返回
			
		nxt = tree[now].data < x ? 1 : 0;//判断左儿子还是右儿子
			
		now = tree[now].son[nxt];
	}
		
	return 0;
}

这个节点要是出现次数大于 1，那好办，直接将其数量减 1 即可。

若是只有 1 次，必然将其转换到叶子节点，不然会对他的子树造成严重影响。

考虑两种情况：

1.没有做左儿子，由于我们已经将该节点转到根节点，相当于这个 \(BST\) 已经变成一条链，那么我们只需要将其直接删除，把他的右儿子换成根节点即可。

2.有左儿子，我们搜寻其左儿子里面的最大值，然后将他转到根节点，因为目标节点的左儿子的最大值必然是个叶子节点，将其转到根节点，相当于将目标节点转移到了叶子节点，但是我们同时要先将目标节点的右儿子变成其儿子才可，最后直接删除即可。

代码：

inline void pop(int x) {
	int node = findd(x);
		
	if (! node) return ;
		
	tot --;
		
	if (tree[node].cnt > 1) {
		tree[node].cnt --, tree[node].sum --;
			
		return ;
	}
		
	if (! tree[node].son[0]) {
			root = tree[node].son[1];
			tree[root].f = 0;
	} else {
		int lmax = tree[node].son[0], rson = tree[node].son[1];
			
		while (tree[lmax].son[1]) lmax = tree[lmax].son[1];//搜寻node节点的左儿子的最大值
			
		splay(lmax, root);//将lmax旋转到根
			
		connect(rson, lmax, 1);//将rson变成lmax的右儿子
		connect(lmax, 0, 1);//让lmax变成0号节点的右儿子，这样就可以让node变为叶子节点
			
		update(lmax);//旋转后修改值
	}
		
	delte(node);//删除
}

3.查询 x 的排名

这个相对来说还是好理解的。

考虑由 x 的大小决定左右子树走向。

若是小于，走右子树，那么这个时候，我们就需要将排名加上左子树的大小了，因为，右儿子肯定比左子树里的所有数大。

若是最后搜到了，上面的加上其左子树大小再加 1 即可。

代码：

inline int qxrank(int x) {
	int ans = 0, nxt, now = root;
		
	while (now) {
		if (tree[now].data == x) {//查询到x
			int rank = ans + tree[tree[now].son[0]].sum + 1;//x的排名即为ans+当前子树大小+1
				
			splay(now, root);
				
			return rank;
		}
			
		nxt = tree[now].data < x ? 1 : 0;
			
		if (nxt) ans += tree[tree[now].son[0]].sum + tree[now].cnt;//若为右儿子则要算上右子树的大小
			
		now = tree[now].son[nxt];
	}
		
	return ans;
}

4.查询排名为 x 的数

考虑逐次递减。

首先先算当前节点的排名，只需用其子树大小加次数即可。

那么这边我们用两个变量 \(num\) 和 \(rank\)，分别来表示没有算其频率和算了其频率的排名。

那么显然，当 \(rank < x\) 的时候，我们当前这个数小了，所以转到右子树，将 x 减去 \(rank\)。

或者 \(num > x\) 的时候，当前数必然大了，就转到左子树搜索。

剩下的，肯定就是频率问题，相当于符合条件，返回即可。

代码：

inline int qrankx(int x) {
	int now = root, rank, num;//当前节点，当前节点的排名(算当前节点出现次数)，当前节点的排名(不算这个节点的数值出现次数)
		
	while (1) {
		num = tree[tree[now].son[0]].sum;
		rank = num + tree[now].cnt;
			
		if (rank < x) now = tree[now].son[1], x -= rank;//如果说rank小于了当前排名，num必然小于，我们就将其转到右儿子搜索
		else if (num >= x) now = tree[now].son[0];//如果说num都大于等于当前排名，rank必然大于，我们就将其转到左儿子
		else {
			splay(now, root);
				
			return tree[now].data;
		}//否则为满足情况
	}
}

5.查询前驱和后继

这两个差不多，这里讲讲前驱。（其实我懒）

定义变量 res，表示前驱。

那么当我们当前节点小于 x 却大于 res 时候，我们就可以将 res 往前提。

那么当我们当前节点大于等于 x 时，我们要走左子树。

看着这个等号很怪，但其实仔细想想，若是等于的时候走右子树，找到的肯定比 x 大，但我们的目标是要比 x 小，故走左子树。

代码：

inline int pre(int x) {
	int now = root, res = -inf;
		
	while (now) {
		if (tree[now].data < x && tree[now].data > res) res = tree[now].data;//当前节点保证比其小，却比res大，才可接着逼近
			
		int nxt = tree[now].data >= x ? 0 : 1;//若是等于，走左儿子，才会取到比x更小，才会走到前驱。
			
		now = tree[now].son[nxt];
	}
		
	return res;
}//前驱
	
inline int nxt(int x) {
	int now = root, res = inf;
		
	//cout << now << endl;
		
	while (now) {
		//cout << tree[now].data << endl;
			
		if (tree[now].data > x && tree[now].data < res) res = tree[now].data;//和前驱相反
			
		int nxt = tree[now].data > x ? 0 : 1;//比x大，才可往左儿子走，以缩小范围。
			
		now = tree[now].son[nxt];
	}
		
	return res;
}//后继

三：FHQ