字符串

字符串简介

字符串，顾名思义，就是由字符连接而成的序列。

常见的字符串问题包括字符串匹配问题，子串相关问题，子序列相关问题，前后缀相关问题，回文串问题，字符串构造问题，border 相关问题等。

字符串基础

字符集

一个字符集 \(\Sigma\) 是一个建立了 全序 关系的集合，也就是说，\(\Sigma\) 中任意两个不同的元素 \(\alpha\) 和 \(\beta\) 都可以比较大小，即 \(\alpha<\beta\) 或 \(\alpha>\beta\)。字符集中的元素称为 字符。

字符串

一个字符串 \(S\) 是将 \(n\) 个字符顺序排列形成的序列，\(n\) 称为 \(S\) 的 长度，表示为 \(|S|\)。

一般来讲字符串下标从 \(1\) 开始计算，\(S\) 的第 \(i\) 个字符记为 \(S[i]\)。

子串

字符串 \(S\) 的子串 \(S[i...j], i<j\)，表示 \(S\) 串从 \(i\) 到 \(j\) 这一段，也就是顺序排列 \(S[i], S[i + 1], ..., S[j]\) 形成的字符串。

当 \(i > j\) 时，\(S[i...j]\) 表示空串。

子序列

字符串 \(S\) 的 子序列 是从 \(S\) 中提取出若干元素并不改变相对位置形成的序列，即 \(S[p_1], S[p_2], ..., S[p_k]\)，\(1\le p_1<p_2<...<p_k\le |S|\)。

后缀

后缀 是指从某个位置 \(i\) 开始到整个串末尾结束的一个特殊子串。字符串 \(S\) 的从 \(i\) 开头的后缀表示为 \(Suffix(S, i)=S[i...|S|]\)。

真后缀 是指除了 \(S\) 本身的所有后缀。

前缀

前缀 是指从串首开始到某个位置 \(i\) 结束的的一个特殊子串。字符串 \(S\) 的以 \(i\) 结尾的前缀表示为 \(Prefix(S, i)=S[1,...,i]\)。

真前缀 是指除了 \(S\) 本身的所有前缀。

字典序

以第 \(i\) 个字符作为第 \(i\) 关键字进行大小比较，特别的，空字符小于字符集内任何字符。

例如：abc\(<\)adc, ab\(<\)abcd。

回文串

回文串 是正着写和倒着写相同的字符串，即对于所有 \(1\le i\le |S|\)，满足 \(S[i]=S[|S|+1-i]\)。

汉明距离

汉明距离 是两个等长字符串的距离，它表示两个长度相同的字符串对应字符不同的数量。

特别的，对于 0/1串，汉明距离为两串异或结果中 \(1\) 的数量。

字符串的存储

字符串主要有两种存储方式。

一种是使用 char 数组存储，使用空字符 \0 表示字符串的结尾（C语言风格字符串）。

另一种是使用C++标准库提供的 string 类。

字符串匹配

字符串匹配问题

定义

又称 模式匹配（pattern matching）。该问题可以概括为「给定字符串 \(S\) 和 \(T\)，在主串 \(S\) 中寻找子串 \(T\) 」。子串 \(T\) 称为 模式串（pattern）。

类型

单串匹配：给定一个模式串 \(T\) 和一个待匹配串 \(S\)，找出前者在后者中的所有位置。

多串匹配：给定多个模式串 \(\{T_i\}\) 和一个待匹配串 \(S\)，找出这些模式串在后者中的所有位置。

• 出现多个待匹配串时，将它们直接连起来便可作为一个待匹配串处理。

• 可以直接当做单串匹配，但是效率不够高。

其他类型：例如匹配一个串的任意后缀，匹配多个串的任意后缀……

单串匹配问题

暴力做法

枚举匹配开始的位置 \(i\)，对于所有的 \(1\le j\le |T|\)，比较 \(S[i + j - 1]\) 与 \(T[j]\) 是否相等，时间复杂度为 \(O(nm)\)。其中，\(n\) 为待匹配串 \(S\) 的长度，\(m\) 为模式串 \(T\) 的长度。

字符串哈希

字符串哈希的本质是对暴力的做法的优化。

考虑暴力做法的复杂度瓶颈，首先枚举匹配开始的位置 \(O(n)\) 次，其次对 \(T\) 进行字符匹配 \(O(m)\) 次，因此其总复杂度为 \(O(nm)\) 的。

枚举匹配开始的位置看上去难以优化，因此我们把目光放在优化字符匹配上去。

字符串哈希就是一种能够 \(O(1)\) 判断两个字符串是否匹配/相等的算法。（注意：这里的用词是 \(O(1)\) 判断，不包含预处理复杂度）

哈希函数

定义一个将字符串映射到整数的函数 \(f\)，我们希望通过判断 \(f(S)\) 与 \(f(T)\) 是否相等来判断两个字符串是否相等。

具体来说，哈希函数需要满足以下两条性质：

• 当 Hash 函数值不一样时，两个字符串一定不一样。（即两个字符串相同时，其 Hash 函数值一定相同）

• 当 Hash 函数值一样时，两个字符串可能一样（但有大概率一样，且我们当然希望它们总是一样的）。

我们将 Hash 函数值相同但原字符串不同的现象称为 哈希碰撞。

通常来讲我们采用 多项式哈希 的方法，具体的，对于一个长度为 \(n\) 的字符串，我们将其看作一个 \(n\) 位的 \(b\) 进制数，定义哈希函数 \(f(S)=\sum_{i = 1}^{n} S[i] \times b^{n - i} \pmod{M}\)。其中模数 \(M\) 是为了缩小函数的值域，确保比较在 \(O(1)\) 的复杂度下完成。

例如对于字符串 \(xyz\)，其哈希函数为 \(xb^2+yb+z \pmod{M}\)。

有时为了方便起见，我们会使用 unsigned long long 定义 Hash 函数的结果。由于 C++ 自然溢出的特性，相当于取模数为 \(2^{64}\)。这也是个不错的选择，因为 自然溢出 的计算效率远高于取模运算。（但由于模数不是质数，自然溢出的哈希碰撞概率较大）

有关哈希碰撞的概率分析可以参考 oi-wiki，我们只需要知道进制 \(b\) 和模数 \(M\) 取质数是碰撞概率较小即可。

多值哈希

如果比较次数很多，哈希碰撞的概率还是很大的，为了解决这一问题，我们可以使用多值哈希的方法。

多值哈希就是取 \(k\) 个不同的模数，分别计算 \(k\) 个哈希值。如果两个字符串相等，那么这 \(k\) 个哈希值全部对应相等；如果存在一个哈希值不等，那么这两个字符串一定不同。

双值哈希可以在保证效率的情况下很好的降低哈希碰撞概率。

多次询问子串哈希

根据多项式哈希的计算公式，我们发现单次计算一个字符串的哈希值复杂度为 \(O(n)\)，如果需要多次询问子串的哈希值，每次重新计算的效率十分低下。

考虑预处理每个 前缀 的哈希值，即预处理 \(h_i=\sum_{j=1}^i S[j]\times b^{i-j}\)。

由于多项式哈希的本质是计算 \(b\) 进制数，因此有递推公式：

\[h_i=h_{i-1}\times b+S_i \]

现在我们利用类似前缀和的方式快速求出 \(f(S[l,...,r])\)，按照定义

\[f(S[l,...,r])=\sum_{j=l}^rS[j]\times b^{r-j} \]

仔细观察 可以发现

\[f(S[l,...,r])=h_{r} - h_{l - 1}\times b^{r - l + 1} \]

因此，可以利用递推公式 \(O(n)\) 预处理前缀哈希值，之后我们可以 \(O(1)\) 查询子串哈希值。

const int max1 = 1e5, base = 29, mod = 1e9 + 7;
struct Hash
{
    int h[max1 + 5], power[max1 + 5];

    void Build ( const char *s, int len )
    {
        h[0] = 0, power[0] = 1;
        for ( int i = 1; i <= len; i ++ )
        {
            h[i] = h[i - 1] * base + (s[i] - 'a' + 1);
            power[i] = 1LL * power[i - 1] * base % mod;
        }
    }

    int Query ( int L, int R )
    {
        return (h[R] - 1LL * h[L - 1] * power[R - L + 1] % mod + mod) % mod;
    }
};

做法

讲了这么多，我们终于可以解决单串匹配问题了！

对于模式串 \(T\) 和待匹配串 \(S\)，预处理 \(S\) 的前缀哈希值，计算 \(T\) 的哈希值。枚举 \(S\) 中的起始匹配位置 \(i\)，查询 \(S[i,...,i+|T|-1]\) 的哈希值，比较其是否与 \(T\) 的哈希值相等即可，时间复杂度 \(O(n+m)\)。

例题

[NOIP2020] 字符串匹配

典型的字符串哈希题目。

枚举 \(AB\) 的长度 \(L\)，枚举 \(AB\) 的重复次数 \(c\)，使用字符串哈希的方法判断重复的 \(c\) 个子串 \(AB\) 是否完全相等，此时我们可以确定字符串 \(C\)。

通过预处理后缀中出现奇数次的字符数量可以 \(O(1)\) 得到字符串 \(C\) 中出现奇数次的字符数量，记这个数量为 \(lim\)，预处理复杂度 \(O(n)\)。

接下来我们计算有多少个小于 \(L\) 的前缀 \(A\)，满足前缀中出现奇数次的字符数量小于等于 \(lim\)。

设 \(f_{i, j}\) 表示小于 \(i\) 的前缀中，出现奇数次的字符数量小于等于 \(j\) 的前缀数量，预处理 \(f_{i, j}\) 数组，这部分复杂度为 \(O(n|\Sigma|)\)。

由于枚举重复次数 \(c\le \tfrac{n}{L}\)，根据调和级数，枚举复杂度为 \(O(n\log n)\)。

总复杂度为 \(O(n\log n+n|\Sigma|)\)。

KMP 算法

前缀函数

给定一个长度为 \(n\) 的字符串 \(S\)，其 前缀函数 被定义为一个长度为 \(n\) 的数组 \(\pi\)，其中 \(\pi[i]\) 的定义为：

• 如果子串 \(S[1, ..., i]\) 中有一段相等的真前缀和真后缀：即 \(S[1, ..., k]\) 和 \(S[i - k + 1, ..., i]\)，那么 \(\pi[i]\) 等于这个相等的真前缀的长度，即 \(\pi[i]=k\)。

• 如果有多个相等的真前缀和真后缀，则 \(\pi[i]\) 取长度最长的一对。

• 如果没有相等的，则 \(\pi[i]=0\)。

特别的，规定 \(\pi[1]=0\)。

对于一个字符串，其相等的前缀和后缀又被称为 border。

举例来说，对于字符串 abcabcd，

\(\pi[1]=0\)，因为 a 没有真前缀和真后缀，根据规定为 \(0\)。

\(\pi[2]=0\)，因为 ab 无相等的真前缀和真后缀。

\(\pi[3]=0\)，因为 abc 无相等的真前缀和真后缀。

\(\pi[4]=1\)，因为 abca 只有一对相等的真前缀和真后缀：a，长度为 \(0\)。

\(\pi[5]=2\)，因为 abcab 相等的真前缀和真后缀只有 ab，长度为 \(2\)。

\(\pi[6]=3\)，因为 abcabc 相等的真前缀和真后缀只有 abc，长度为 \(3\)。

\(\pi[7]=0\)，因为 abcabcd 无相等的真前缀和真后缀

同理可以计算字符串 aabaaab 的前缀函数为 \([0, 1, 0, 1, 2, 2, 3]\)。

计算前缀函数

按照 \(i=1, 2, ..., n\) 的顺序，依次计算 \(\pi[i]\)。

考虑如何求解 \(\pi[i]\)，根据 \(\pi\) 的定义，\(\pi[i]\) 为 \(S[1, ..., i]\) 中 border 的最大长度，设 \(\pi[i]=j\)，则 \(S[1, ..., j]=S[i - j + 1, i]\)。

那么显然有 \(S[1, ..., j - 1]=S[i - j + 1, i - 1]\)。

此时，一种显然的想法是遍历 \(S[1, ..., i - 1]\) 所有 border，即遍历所有满足 \(S[1, ..., k] = S[i - k, i - 1]\) 的 \(k\)，判断 \(S[k + 1]\) 与 \(S[i]\) 的相等关系，更新 \(\pi[i]\)。

考虑如何遍历 \(S[1, ..., i - 1]\) 的所有 border，首先取最大的 \(\pi[i - 1]\)。

考虑由于次小的满足 \(S[1, ..., k]=S[i - k, i - 1]\)，由于 \(S[1, ..., \pi[i - 1]]=S[i - \pi[i - 1], i - 1]\)，容易发现 \(k\) 也是 \(S[1, ..., \pi[i - 1]]\) 中一个 border 的长度。

因此，初始化 \(j=\pi[i - 1]\)，依次遍历 \(j = \pi[j]\) 即可。

这里放个图帮助大家理解。

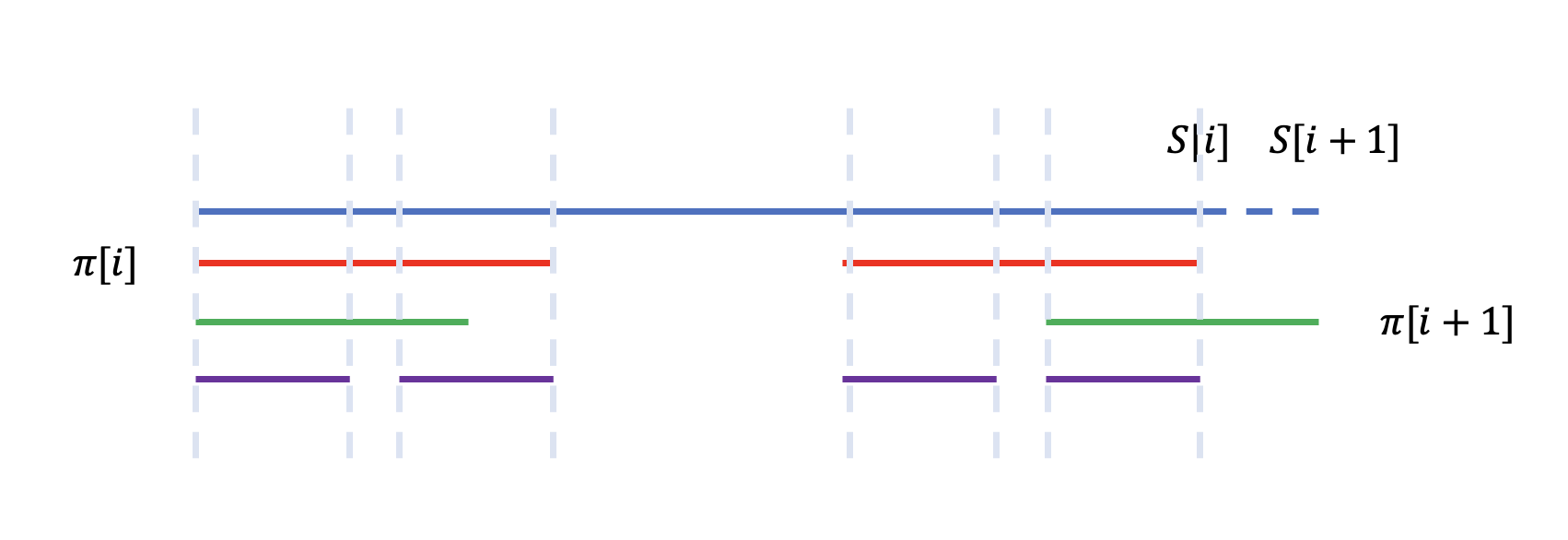
pi[1] = 0;
for ( int i = 2, j = 0; i <= n; i ++ )
{
    while ( j && s[j + 1] != s[i] )
        j = pi[j];
    
    if ( s[j + 1] == s[i] )
        ++j;
    pi[i] = j;
}

接下来分析 KMP 算法的复杂度。

观察代码，\(j\) 在每次 for 循环中最多加 \(1\)，因此 \(j\) 的总势能为 \(O(n)\)，即 while 循环最多进行 \(O(n)\) 次，时间复杂度为 \(O(n)\)。

做法

利用前缀函数，我们可以高效地解决单串匹配问题。

设模式串为 \(T\)，长度为 \(m\)，待匹配串为 \(S\)，长度为 \(n\)，令 P = T + # + S。其中，# 是 \(T\) 和 \(S\) 中都没有的特殊字符。

对 \(P\) 求前缀函数，当枚举的位置 \(i> m+1\) 时，判断 \(\pi[i]\) 是否等于 \(m\) 即可，复杂度为 \(O(n + m)\)。

事实上，由于 \(\pi[i]\le m\)，因此记录前 \(m\) 个位置的前缀函数值即可，空间复杂度为 \(O(m)\)。（当然很少有出题人卡这个）

多串匹配问题

多串匹配问题我们只需要考虑多模式串匹配，即由多个模式串 \(\{T_i\}\) 和一个待匹配串 \(S\)，求解每个 \(T_i\) 在 \(S\) 中的出现次数。（因为如果有多个待匹配串，我们可以简单拼接转化成一个待匹配串）

前置：字典树（Trie 树）

定义

字典树（英文名：Trie）。顾名思义，就是一个像字典一样的树。

引入

字典树的思想非常简单，大家只需要回想一下自己查阅英语词典的过程就能掌握字典树的本质。

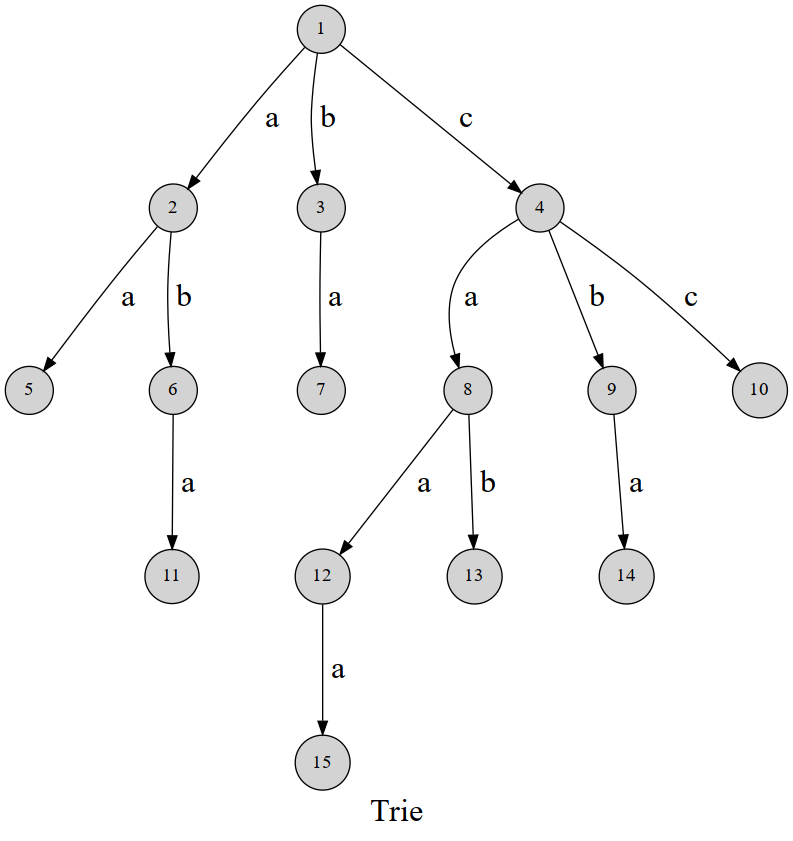
可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子 \(1\to4\to 8\to 12\) 表示的就是字符串 caa。

Trie 的结构非常好懂，我们用 \(\delta(u,c)\) 表示结点 \(u\) 的 \(c\) 字符指向的下一个结点，或着说是结点 \(u\) 代表的字符串后面添加一个字符 \(c\) 形成的字符串的结点。（\(c\) 的取值范围和字符集大小有关，不一定是 \(0\sim 26\)）

有时需要标记插入进 trie 的是哪些字符串，每次插入完成时在这个字符串所代表的节点处打上标记即可。

实现

struct Trie
{
    int tree[max1 + 5][26];

    void Clear ()
    {
        memset(tree[0], 0, sizeof(tree[0]));
        return;
    }

    void Insert ( const char *s, int len )
    {
        int now = 0;
        for ( int i = 1; i <= len; i ++ )
        {
            if ( !tree[now][s[i] - 'a'] )
            {
                tree[now][s[i] - 'a'] = ++total;
                memset(tree[total], 0, sizeof(tree[total]));
            }
            now = tree[now][s[i] - 'a'];
        }
        return;
    }
};

例题

最长异或路径

由于异或运算满足交换律和结合律，因此任意两点 \(u, v\) 的简单路径的异或和 \(=\) \(u\) 到根的简单路径的异或值 \(\operatorname{xor}\) \(v\) 到根的简单路径的异或值。

那么可以将题意转化为给定 \(n\) 个数，从中选择两个数，求其异或值的最大值。

我们考虑每次依次把每个数插入到一个 0/1 Trie 上。

0/1 Trie 就是对只有 01 的二进制数建 Trie，每个二进制都看成只有 0 和 1 的字符串。

考虑从 Trie 的根开始往下走，如果当前位是 0 就尽量走 1 边，当前位是 1 就尽量走 0 边，如果想走的边不存在那就走存在的边。

按照从高位向低位贪心的做法，很容易算出异或值的最大值。

复杂度 \(O(n\log w)\)。

AC 自动机

前置：自动机（DFA）

DFA 可以看作一张有向图，图上的顶点代表 DFA 上的一个状态。

DFA 的作用就是 识别字符串，一个自动机 \(A\)，若它能识别（接受）字符串 \(S\)，那么 \(A(S)=\mathrm{True}\)，否则 \(A(S)=\mathrm{False}\)。

当一个 DFA 读入一个字符串时，从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态，那么我们称这个 DFA 接受 这个字符串，反之我们称这个 DFA 不接受 这个字符串。

看起来非常晦涩难懂，大家仅做了解即可。（事实上我也不懂）

概述

AC（Aho–Corasick）自动机 是 以 Trie 的结构为基础，结合 KMP 的思想 建立的自动机，用于解决 多模式匹配 等任务。

AC 自动机本质上是 Trie 上的自动机。

简单来说，建立一个 AC 自动机有两个步骤：

• 基础的 Trie 结构：将所有的模式串构成一棵 Trie；

• KMP 的思想：对 Trie 树上所有的结点构造失配指针。

建立完毕后，就可以利用它进行多模式匹配。

失配指针

多模式串匹配是单模式串匹配问题的扩展，因此考虑如何在 Trie 上引入 KMP 思想。

我们可以在 Trie 上定义一个与 \(\pi\) 数组类似的 \(\operatorname{fail}\) 数组，这个数组也被称为失配指针。

具体的，定义 \(\operatorname{fail}(u)\) 表示 \(u\) 表示的字符串 最长的 且出现在 Trie 中的 真后缀。

特别的，如果不存在这样的真后缀，则 \(\operatorname{fail}\) 为 \(0\)（指向跟节点）。

不难发现，当 Trie 中只有一个模式串时，\(\operatorname{fail}\) 就是 KMP 中的 \(\pi\) 数组。

由于每个点只有唯一的 \(\operatorname{fail}\) 指针且指向深度更小的点，因此 \(\operatorname{fail}\) 构成一棵树。

构建 AC 自动机

首先构建 Trie 树，接下来考虑求解 失配指针。

我们通过 Bfs 的方式构建 AC 自动机。

考虑求解 \(u\) 节点的 \(\operatorname{fail}\)，类似 KMP，我们只需要遍历 \(\operatorname{farther}(u)\) 的所有 \(\operatorname{fail}\) 节点，判断其在 Trie 树上能否扩展即可。

然而 KMP 对应的 Trie 树是一个链式结构，其每个节点的势能只能传递到 唯一的一个节点；然而在普通的 Trie 树中，每个节点的势能可能传递到 多个节点，因此会产生 势能分裂 的现象。因而均摊分析不再适用，暴力跳 \(\operatorname{fail}\) 的做法不再适用。

事实上只需要维护转移函数

\[\delta(u, c)= \begin{cases} u + 1 & tr_{u, c}\text{ exists}\\ 0 & tr_{u, c}\text{ does not exist}\ \wedge\ u = 0\\ \delta(\operatorname{fail}(u), c) & tr_{u, c}\text{ does not exist}\ \wedge\ u \ne 0 \end{cases} \]

容易发现，\(\operatorname{fail}(u)=\delta(\operatorname{fail}(\operatorname{father}(u)), c)\)。

因此我们可以在 \(O(|\Sigma|n)\) 的时间复杂度内建立 AC 自动机。

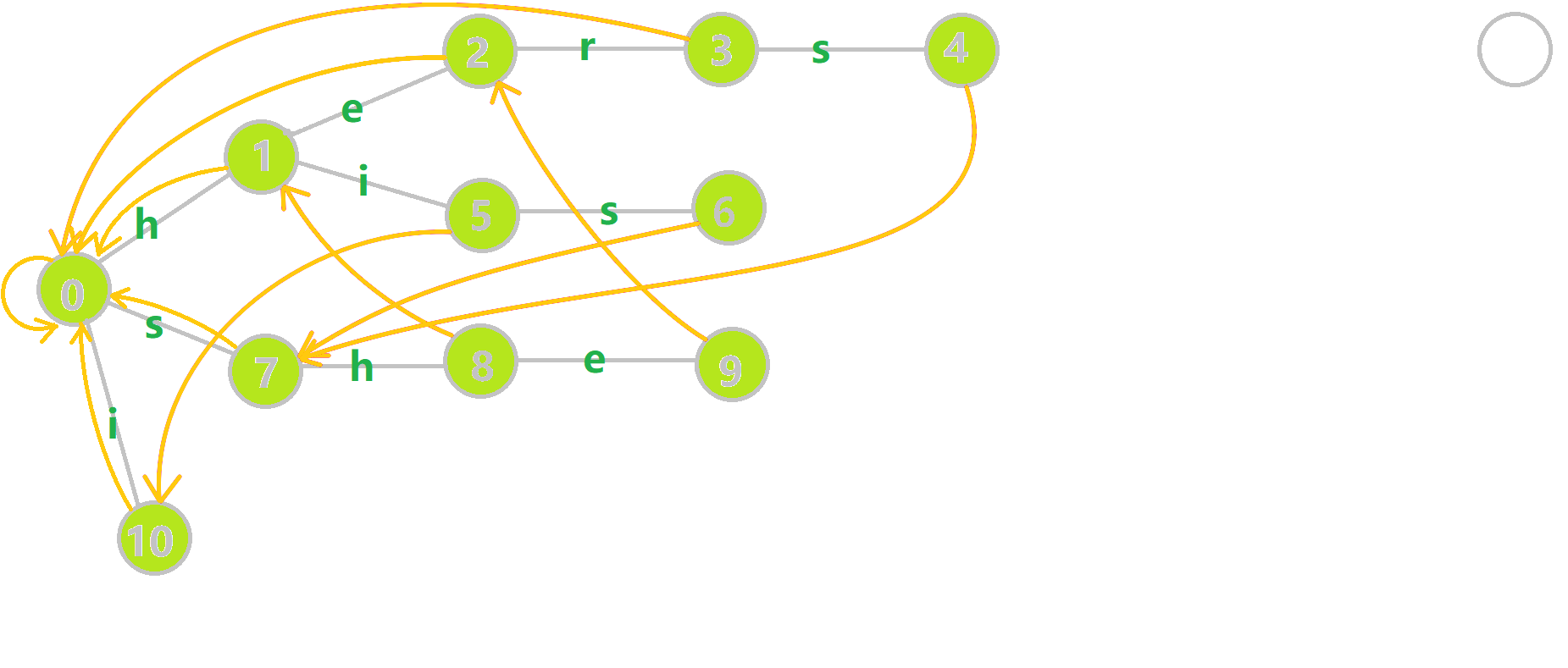
struct Aho_Corasick_automaton
{
    struct Struct_Aho_Corasick_automaton
    {
        int fail, son[26];
    } tree[max1 + 5];
    int q[max1 + 5], l, r;
    void Insert(char *s, int id)
    {
        int len = strlen(s + 1), now = 0;
        for (int i = 1; i <= len; i++)
        {
            if (!tree[now].son[s[i] - 'a'])
                tree[now].son[s[i] - 'a'] = Create(now);
            now = tree[now].son[s[i] - 'a'];
        }
        return;
    }
    void Build()
    {
        for (int i = 0; i < 26; i++)
        {
            if (tree[0].son[i])
                q[++r] = tree[0].son[i];
            tree[tree[0].son[i]].fail = 0;
        }
        while (l <= r)
        {
            int now = q[l++];
            for (int i = 0; i < 26; i++)
            {
                if (!tree[now].son[i])
                    tree[now].son[i] = tree[tree[now].fail].son[i];
                else if (tree[now].son[i])
                {
                    tree[tree[now].son[i]].fail = tree[tree[now].fail].son[i];
                    q[++r] = tree[now].son[i];
                }
            }
        }
        return;
    }
} AC;

多模式串匹配

将所有模式串 \(\{T_i\}\) 插入到 Trie 树中，构建 AC 自动机。

之后将待匹配串 \(S\) 输入到 AC 自动机，记录每个节点走过的次数 \(cnt_i\)。

容易发现每个到达的节点 \(u\) 代表 待匹配串 \(S\) 的当前前缀 \(S[1, ..., i]\) 能够在模式串 Trie 树中匹配的最大 后缀。

由于 \(S[1, ..., i]\) 能够匹配的位置，就是当前节点 \(u\) 在 \(\operatorname{fail}\) 树上的所有祖先节点，因此一个模式串在带匹配串中的出现次数就是该模式串串尾对应节点子树中 \(cnt\) 的和。