多校数据结构

多校数据结构

省选选手不再需要学习新数据结构，主要需要学习数据结构题目的常见套路，训练代码能力，提升思维能力。

因此，此次授课主要提供各种类型的数据结构题目，点拨解题思路，为选手在比赛中处理各类数据结构问题提供参考。

[CF1039D] You Are Given a Tree

题目描述

有一棵 \(n\) 个节点的树。

其中一个简单路径的集合被称为 \(k\) 合法当且仅当：

树的每个节点至多属于其中一条路径，且每条路径恰好包含 \(k\) 个点。

对于 \(k\in [1,n]\)，求出 \(k\) 合法路径集合的最多路径数即：设 \(k\) 合法路径集合为 \(S\)，求最大的 \(|S|\)。

\(n \leq 10^5\)。

题解

首先考虑暴力，比较显然的贪心是直接 dfs ，能拼成链就拼。

正解考虑根号分治对于 \(k\le B\) 的答案，我们直接暴力求解，复杂度为 \(O(nB)\) 。

对于 \(k\ge B\) 的答案，我们发现最终答案一定小于等于 \(\lfloor\tfrac{n}{B}\rfloor\) ，而且答案一定随 \(k\) 增大而单调递减，因此我们可以枚举答案，使用二分的方法求解当前答案所对应的 \(k\) 的区间，复杂度为 \(O(\tfrac{n^2}{B}log n)\) 。

简单平衡后，复杂度为 \(O(n\sqrt{n\log n})\) 。

[AGC001F] Wide Swap

题目描述

给出一个元素集合为 \(\{1,2,\dots,N\}\) \((1\leq N\leq 500,000)\) 的排列 \(P\)，当有 \(i,j\) \((1\leq i<j\leq N)\) 满足 \(j-i\geq K\) \((1\leq K\leq N-1)\) 且 \(|P_{i}-P_{j}|=1\)时，可以交换 \(P_{i}\) 和 \(P_{j}\)。

求：可能排列中字典序最小的排列。

题解

考虑求解 \(pos\) 数组，其中 \(pos_i\) 满足原排列中 \(P_{pos_i}=i\) 。

简单进行题意转化，发现相邻的 \(pos_i, pos_{i + 1}\) ，如果 \(|pos_i - pos_{i + 1}|\ge K\) ，那么可以交换。

字典序最小就是使得 \(pos\) 数组中 \(1\) 所在位置最小，然后 \(2\) 所在位置最小，然后 \(3\) 所在位置最小。

此时容易发现若原 \(pos\) 序列中存在两个 \(pos_i, pos_j\) ，满足 \(|pos_i - pos_j| < K\) ，那么最终的 \(pos\) 序列中， \(pos_i, pos_j\) 在序列中的相对位置不会发生改变。

一个比较显然的做法是若 \(|pos_i - pos_j| < K\ and\ i < j\) ，那么我们从 \(pos_i\) 向 \(pos_j\) 连接一条有向边。此时得到的图是一个 DAG ，我们需要做的就是给每个点合理的拓扑编号，使得最终的拓扑编号的字典序最小。

考虑用优先队列维护所有入度为 \(0\) 的点，每次取出最小的点进行拓扑排序。

然而对于普通的 DAG 来说，上述做法并不正确。

考虑如下一种情况：

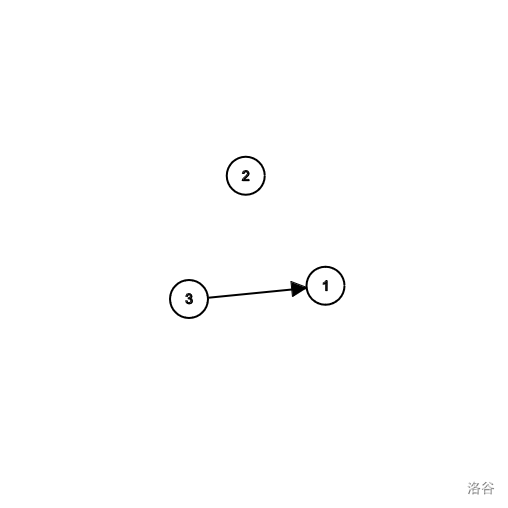
如果使用上述算法得到的拓扑编号为 \(3, 1, 2\) 。

然而实际上字典序最小的拓扑编号为 \(2, 3, 1\) 。

我们建立反拓扑图，每次取最大的进行拓扑排序，然后将拓扑编号整个反转即可。

然而本题采用第一种做法同样可以通过，这利用了本题拓扑图的特殊性，详细分析可以参考 https://www.cnblogs.com/PinkRabbit/p/AGC001F.html ，这里不再赘述。

但是拓扑图边数为 \(O(nK)\) ，不能直接建图，考虑优化。

考虑我们取出的当前点为 \(i\) ，那么 \(i\) 向所有满足 \(|i - j| < K\ and\ P_i > P_j\) 的所有 \(j\) 连边，因此不妨用线段树维护每个点的入度，删去 \(i\) 时我们只需要对区间 \([i - K + 1, i + K - 1]\) 所有值减 \(1\) 。

但这忽略了对满足 \(|i - j| < K\ and\ P_i < P_j\) 的 \(j\) 的影响，此时发现一定存在 \(j\) 到 \(i\) 的边，因此 \(j\) 一定已经被赋予了拓扑编号，可以维护线段树时给已经赋予拓扑编号的点修改入度为 \(\inf\) 。

[CF1578B] Building Forest Trails

题目描述

在密林的中央，\(n\) 个村庄坐落在一个巨大的圆上，将圆环顺次 \(n\) 等分。自远古以来，从一个村庄旅行到另一个村庄是不可能完成的，任意两个村庄之间都互不连通。现在，我们有了新的技术，可以在密林当中开展工程，来让某些村庄之间联通。

工程包括 \(m\) 个操作，分为建设一条道路和查询某两个村庄是否联通两类。一条道路是一条连接某两个村庄的线段，在道路被修建后，该条道路两端的村庄的人将可前往另端的村庄，即，这两个村庄将彼此联通。类似的，若村庄 \(a\) 到 \(b\) 联通，\(b\) 到 \(c\) 联通，那么 \(a\) 到 \(c\) 也将联通。

更进一步的，若两条道路在圆中交叉，那么任何人都将可以通过交叉所形成的岔路口。即，岔路口的两条路径两端的四个村庄也将彼此联通。我们给出一个例子：若村庄被沿顺时针顺序以 \(1\) 到 \(6\) 顺次标号，并且我们修建了 \(1\) 到 \(3\) ，\(2\) 到 \(4\) 和 \(4\) 到 \(6\) 的路径，那么除去 \(5\) 号村庄之外的所有村庄都将联通。

给出 \(m\) 个操作，你需要回答其中的全部询问。

\(2 \le n \le 2·10^5,\ 1 \le m \le 3·10^5\)

输入共 \(m+2\) 行。

• 第一行两个整数 \(n,m\)，意义如题面所示。
• 接下来的 \(m\) 行， 每行三个整数 \(e(e\in \{1,2\}),v(1\le v\le n),u(1\le u \le n)\)。
  • 若 \(e=1\)，即为修建一条 \(v\) 到 \(u\) 的道路。
  • 若 \(e=2\)，查询 \(v\) 到 \(u\) 是否联通。

输出共一行。 输出一个字符串 \(s\)，其中 \(s_i\) 代表第 \(i\) 个查询操作的答案，下标从1开始。

题解

很容易有一个非常暴力的思路，枚举之间添加的所有道路，判断是否与当前修建道路有交，用并查集暴力维护。

简单观察发现，一个连通块内的连边情况并不重要，我们可以仅通过连通块内的点和当前修建的道路来判断两个连通块是否需要合并。

例如，如果 \(1, 3, 7, 9\) 是连通的，我们不在乎连通它们的边是 \(1-7, 3-9\) 或 \(1-3, 1-7, 1-9\) 或 \(1-3, 3-7, 7-9\) ，我们只需要找到集合中是否存在一个点 \(C\) ，满足 \(A\le C\le B\) ，其中 \(A, B\) 为当前修建的道路的两端。只要存在点 \(C\) ，那么当前修建的道路一定与集合中某条边有交。

因此对于一个连通块，我们选择一个特殊的连边方式，比如对于 \(1, 3, 7, 9\) ，我们选择连边 \(1-3, 3-7, 7-9\) 。

这样连边，我们可以断环为链，例如：

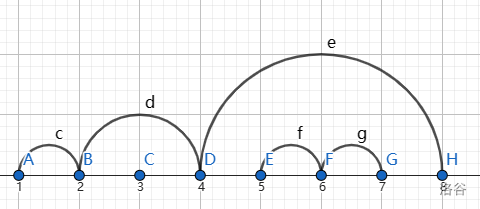
考虑记录数组 \(f_i\) 表示第 \(i\) 个点上有 \(f_i\) 层边。

例如图中 \(f_1=f_2=0, f_3=1, f_4=0, f_5=f_6=f_7=1, f_8=0\) 。

此时考虑加边 \((u, v)\) ，我们分情况讨论：

如果 \(h_u\ne h_v\) ，不妨设 \(h_u > h_v\) ，例如图中的 \(5, 8\) 两点，显然 \((u, v)\) 连边一定会与一个集合有交，我们找到 \(u\) 之后第一个满足 \(h_i < h_u\) 的 \(i\) ，合并 \(i\) 和 \(u\) 所在集合，同时维护 \(h\) 。

如果 \(h_u=h_v\) ，同样尝试找到 \(u\) 之后第一个满足 \(h_i < h_u\) 的 \(i\) ，如果存在并且 \(i\) 小于 \(v\) 所在集合中最小的元素，那么合并 \(i\) 和 \(u\) ，如果不存在，那么当前加入的边不会与其他边产生交点，直接合并 \(u, v\) 即可。

发现每次对 \(h\) 的操作是区间加和查询一个位置后第一个小于某个值的位置，用线段树维护即可。

[CF1129D] Isolation

题目描述

给出一个长度为 \(n\) 的序列 \(A\) ，把它划分成若干段，使得每一段中出现过恰好一次的元素个数 \(\le k\)，求方案数对 \(998244353\) 取模后的结果。

\(1\le n\le 10^5\) 。

题解

很容易定义 dp ，设 \(f_i\) 表示将 \([1, i]\) 划分为若干段，使得每一段中出现过 恰好 一次的元素个数 \(\le k\) 的方案数。

转移有 \(f_i=\sum f_j\) ，其中 \([j + 1, i]\) 为出现过 恰好 一次的元素个数 \(\le k\) 的一段。

考虑维护 \(g_j\) 表示 \([j + 1, i]\) 中出现过恰好一次的元素个数。

从 \(i\) 扩展到 \(i + 1\) ，只需要找到 \(i + 1\) 前面第一个满足 \(a_k = a_{i + 1}\) 的 \(k\) ，对于 \(j\in [k, i]\) ， \(g_j\) 加 \(1\)， 对于 \(j\in [0, k - 1]\) ， \(g_j\) 减 \(1\) 。

发现 \(g\) 每次之后修改 \(O(1)\) 个区间，因此考虑用分块优化 dp 转移。

具体的每个块内维护 \(sum_{x}\) ，表示块内所有满足 \(g_j\le x\) 的 \(f_j\) 之和， \(x\) 的取值范围为 \([l, r]\) ，其中 \(r - l + 1\) 不超过块长，因此对于每个块维护 \(sum, l, r\) 即可。

复杂度为 \(O(n\sqrt{n})\) 。

[AGC015E] Mr.Aoki Incubator

题目描述

数轴上有\(N\)个点，每个点初始时在位置\(X_i\)，以\(V_i\)的速度向数轴正方向前进。

初始时刻，你可以选择一些点为其染色，之后的行走过程中，染色的点会将其碰到的所有点都染上色，之后被染上色的点亦是如此。

在所有\(2^N\)种初始染色方案中，问有多少种初始染色方案，能使得最终所有的点都被染色？答案对\(10^9+7\)取模。

\(1\le N\le 2\times 10^5, 1\le X_i, V_i\le 10^9\) 。

题解

结论：若初始集合为 \(S\) ，最终被标记的点构成的集合为 \(f(S)\) ，有 \(f(S\cup T) = f(S)\cup f(T)\) 。

证明：显然 \(|f(S\cup T)|\ge |f(S)\cup f(T)|\) ，因此假设存在一个元素 \(x\in f(S\cup T)\) 并且 \(x\notin f(S)\cup f(T)\) ，显然 \(x\) 不可能为初始标记的点，设 \(x'\) 为将 \(x\) 标记的点，显然 \(x'\notin |f(S)\cup f(T)|\) ，继而有 \(x'',\ x'''...\notin |f(S)\cup f(T)|\) ，这个过程是无限的，然而集合大小有限，与前提矛盾。

考虑一个点 \(i\) 能够标记那些点，首先所有满足 \(j < i,\ v_j > v_i\) 和满足 \(j > i,\ v_j < v_i\) 的点会被标记，之后位于 \(i\) 左侧的点又回运动到 \(i\) 的右侧标记速度小于它的点，位于 \(i\) 右侧的点又回运动到 \(i\) 的左侧标记速度大于它的点，最后便没有点可以继续标记了。

总结一下，将所有点按照初始坐标排序，设 \(premax_i\) 表示 \([1, i]\) 区间内速度最大值，设 \(sufmin_i\) 表示 \([i, n]\) 区间内速度最小值，那么 \(i\) 可以标记的点为满足 \(j > i,\ v_j < premax_i\) 和满足 \(j < i,\ v_j > sufmin_i\) 的所有点。

考虑 dp ，设 \(f_i\) 表示考虑了前 \(i\) 个点，将 \([1, i]\) 区间全部染色的方案数。

转移考虑枚举下一个初始染色的点 \(j\) ，对于区间 \((i, j)\) 的点，容易发现如果 \(i, j\) 不能将其全部染色，其他点同样无法将其全部染色。

\((i, j)\) 区间内不能被染色的点为位于区间 \((i, j)\) 内，速度满足 \(premax_j\le v\le sufmin_i\) 的点。

由于 \(premax_j\) 单调递增，同时 \((i, j)\) 中点的个数单调递减，因此可以转移的 \(j\) 构成一段连续的区间。

设这段连续的区间为 \([L_i, i - 1]\) ，当 \(i\) 向右扩展时 \(sufmin_i\) 增大，同时区间内元素增多，因此 \(L_i\) 单调递增。

用双指针维护 \(L_i\) 即可。

[BalkanOI2018] Election

题目描述

有一个长度为 \(N\) 的字符串 \(S[1\dots N]\)，它仅由 C 和 T 两种字母组成。
现在有 \(Q\) 个查询，每个查询包含两个整数 \(L\) 和 \(R\)，表示：设新字符串 \(S'=S[L\dots R]\)，至少在 \(S'\) 中要删除多少个字符，才能保证：对于 \(S'\) 的每一个前缀和后缀，其 C 的数量都不小于 T 的数量。

\(1\le N, Q\le 5\times 10^5\) 。

题解

按照比较套路的想法，我们给 C 赋值为 \(1\) ，给 T 赋值为 \(-1\) 。

那么原题的限制变为 \(S'\) 的每个前后缀和均大于等于 \(0\) 。

考虑一种比较显然的贪心，从左到右扫，如果当前前缀和小于 \(0\) ，则删除当前字符，剩余字符串从右到左再扫一次。

从左到右贪心的过程使得删除的位置尽可能靠右，这能够影响更多的后缀，使最终删除的字符最少。

不妨设 \(pre_i\) 表示前 \(i\) 个字符的和， \(suf_i\) 表示后 \(i\) 个字符的和。

容易发现从左到右贪心的过程删去的字符数量为 \(-\min(pre_i)\) ，设 \(suf'_i\) 为删去这些字符后后 \(i\) 个字符的和，那么从右到左的过程删去字符的数量为 \(-\min(suf'_i)\) 。

继续观察发现删去的位置为 \(pre_i\) 第一次为 \(-1,\ -2,\ -3,\ ...\) 的位置，因此得到 \(suf'_i = suf_i - \min(pre_i) + \min_{j < i}(pre_j)\) 。

因此答案为

\[-\min(pre_i) - \min(suf_i - \min(pre_i) + \min_{j < i}(pre_j)) \]

简单化简有

\[-min_{j < i}(suf_i + pre_j) \]

直接用线段树维护最小子段和即可。

[AGC007E] Shik and Travel

题目描述

一颗 \(n\) 个节点的二叉树，每个节点要么有两个儿子要么没有儿子。边有边权。

你从 \(1\) 号节点出发，走到一个叶子节点。然后每一天，你可以从当前点走到另一个叶子。最后回到 \(1\) 号节点，要求到过所有叶子并且每条边经过恰好两次。

每天的路费是你走过的路径上的边权和，你的公司会为你报销大部分路费，除了你旅行中所用路费最高的，行走路线是从叶子到叶子的那一天的路费。

求你自己最少要付多少路费？

\(2 < N < 131072, 0\le v_i\le 131072\) 。

题解

显然最终的答案满足可二分性。

设二分的答案为 \(ans\) ，因此设 \(f(u, x, y)\) 表示是否存在满足以下条件的方案：

1. 从 \(u\) 出发到达第一个叶子结点的距离为 \(x\) ，从 \(v\) 出发到达最后一个叶子结点的距离为 \(y\) 。

2. 所有经过的路径中最大值小于等于 \(x\) 。

3. 能够遍历整棵 \(u\) 子树。

转移显然有 \(f(u, x, y) = \operatorname{or}_{(a, b)} f(v_1, x, a) \& f(v_2, b, y) \& (a + b + val_u\le ans)\) 。

其中 \(val_u\) 表示 \(u\) 的两个儿子的边的权值和。

直接转移复杂度爆炸，考虑优化。

容易发现如果存在 \((x_1, y_1),\ (x_2, y_2)\) ，并且 \(x_1\le x_2,\ y_1\le y_2\) ，那么 \((x_2, y_2)\) 一定不优。

因此考虑删除这样的 \((x_2, y_2)\) ，这样我们得到的二元组中 \(y\) 随 \(x\) 的增大而减小。

考虑合并两个 \(v_1, v_2\) 子树，枚举其中一棵子树的二元组 \((x, a)\) ，发现 \(b\le ans - a - val_u\) ，因此能够产生贡献的 \((b, y)\) 是一段前缀。由于 \(y\) 随 \(b\) 的增大而减小，我们只需要取最后一个最小的 \(y\) 进行合并即可。

同理我们还需要枚举另一棵子树中的 \((x, a)\) 重复以上操作。

设当前合并的两棵子树状态数分别为 \((p, q)\) ，则合并后状态数为 \(2\times\min(p, q)\) ，类似启发式合并，复杂度为 \(O(n\log n)\) ，总复杂度为 \(O(n\log n\log V)\) 。

[CF1146D2] Frequency Problem (Hard Version)

题目描述

给出\(n(1 \le n \le 200000)\)个元素组成的序列\(a_1,a_2,……,a_n\)。

求最长的子段使得其中有至少两个出现次数最多的元素。

输出最长子段长度。

题解

结论：满足至少两个出现次数最多的元素的区间中，出现次数最多的元素构成的集合包含了整个序列的众数。

证明：如果存在一个区间满足条件，并且出现次数最多的元素构成的集合不包含整个序列的众数，那么整个序列的众数在这个区间的出现次数小于这个区间内出现次数最多的元素的出现次数，通过扩展区间，我们一定可以找到一个区间使得整个序列的众数为这个区间的众数，容易发现扩展的新区间更优。

设整个序列的众数为 \(x\) ，考虑枚举区间内另一个众数 \(y\) ，设前 \(i\) 个数中 \(x\) 的出现次数为 \(S_i\) ， \(y\) 的出现次数为 \(T_i\) ，那么满足条件的区间 \([L, R]\) 有 \(S_R - S_{L - 1} = T_R - T_{L - 1}\) ，简单移项有 \(S_R - T_R = S_{L - 1} - T_{L - 1}\) 。枚举区间右端点 \(R\) ，找到最小的左端点即可，复杂度为 \(O(n^2)\) 。

优化考虑根号分治，对于出现次数大于等于 \(\sqrt{n}\) 的数，它们的种类不会超过 \(\sqrt{n}\) 个，可以直接用上述方法解决，对于出现次数小于 \(\sqrt{n}\) 的数，我们可以直接枚举整个序列的众数在区间的出现次数 \(k\) ，然后枚举区间的右端点，只需要找到最小左端点满足有两个区间众数出现了 \(k\) 次即可，容易发现左端点随右端点增大而增大，用双指针维护即可。

Souvenirs

题目描述

• 给出 \(n\) 以及一个长为 \(n\) 的序列 \(a\)。

• 给出 \(m\)，接下来 \(m\) 组询问。

• 每组询问给出一个 \(l,r\)，你需要求出，对于 \(i,j \in [l,r]\)，且满足 \(i \neq j\)，\(|a_i-a_j|\) 的最小值。

• \(1 \leq n \leq 10^5\)，\(1 \leq m \leq 3\times 10^5\)，\(0 \leq a_i \leq 10^9\)

题解

考虑二元组 \((i, j),\ i < j\) ，不妨设 \(a_i < a_j\) ，很容易发现对于 \(k > j,\ a_k > a_j\) ，二元组 \((i, k)\) 一定不优。

继续考虑发现对于 \(k > j,\ a_k > \tfrac{a_i + a_j}{2}\) ，二元组 \((i, k)\) 一定没有 \((j, k)\) 优。

因此对于每个位置 \(i\) ，考虑所有可能贡献答案的 \((i, j)\) ，不妨找到 \(i\) 之后第一个大于 \(a_i\) 的位置 \(j\) ，之后在找到 \(j\) 之后第一个小于 \(\tfrac{a_i + a_j}{2}\) 的位置 \(k\) ，以此类推找到其他位置。容易发现值域区间每次减半，因此最终找到的二元组总数为 \(O(n\log V)\) 。

之后可以直接用扫描线解决，复杂度为 \(O(n\log n\log V)\) 。

[NOI2020] 时代的眼泪

题目描述

小 L 喜欢与智者交流讨论，而智者也经常为小 L 出些思考题。

这天智者又为小 L 构思了一个问题。智者首先将时空抽象为了一个二维平面，进而将一个事件抽象为该平面上的一个点，将一个时代抽象为该平面上的一个矩形。

为了方便，下面记 \((a, b) \leq (c, d)\) 表示平面上两个点 \((a, b),(c, d)\) 满足 \(a \leq c\)，\(b \leq d\)。

更具体地，智者给定了 \(n\) 个事件，他们用平面上 \(n\) 个不同的点 \(\{(x_i, y_i)\}^n_{i=1}\) 来表示；智者还给定了 \(m\) 个时代，每个时代用平面上一个矩形 \((r_{i,1}, r_{i,2}, c_{i,1}, c_{i,2})\) 来表示，其中 \((r_{i,1}, c_{i,1})\) 是矩形的左下角，\((r_{i,2}, c_{i,2})\) 是矩形的右上角，保证 \((r_{i,1}, c_{i,1}) \leq (r_{i,2}, c_{i,2})\)。我们称时代 \(i\) 包含了事件 \(j\) 当且仅当 \((r_{i,1}, c_{i,1}) \leq (x_j, y_j ) \leq (r_{i,2}, c_{i,2})\)。

智者认为若两个事件 \(i, j\) 满足 \((x_i, y_i) \leq (x_j, y_j)\)，则这两个事件形成了一次遗憾。而对一个时代内包含的所有事件，它们所形成的遗憾被称为这个时代的眼泪，而形成的遗憾次数则称为该时代的眼泪的大小。现在智者想要小 L 计算每个时代的眼泪的大小。

小 L 明白，如果他回答不了这个问题，他也将成为时代的眼泪，请你帮帮他。

\(n\le 10^5,\ m\le 2\times 10^5\) 。

题解

著名分块题目。

主要思路是维护数组，疯狂容斥。

设 \(rk_{i, j}\) 表示第 \(i\) 块内排名为 \(j\) 的数。

\(p_{i, j}\) 表示 \(i\) 所在块左端点到 \(i\) 内所有 \(\le rk_j\) 的数的个数。

\(pre_{i, j}\) 表示前 \(i\) 块内 \(\le j\) 的数的个数。

\(lsh_{i, j}\) 表示第 \(i\) 块内 \(\le j\) 的最大排名。

\(c_{i, j, k}\) 表示第 \(i\) 块排名前 \(k\) 个数与前 \(j\) 块产生的顺序对个数。

\(sum_{i, j, k}\) 表示第 \(i\) 块从排名 \(j\) 到排名 \(k\) 之间的顺序对数。

维护比较容易。

考虑查询矩形 \([X_1, X_2, Y_1, Y_2]\) ，分 \(5\) 种情况讨论。

1. 散块内：以左散块为例，设当前暴力枚举的点为 \((x, i)\) ，只需要查询块内 \((i, j)\) 满足 \(i\ge x,\ y\le j\le Y_2\) 。 \(p\) 数组求解即可。

2. 整块内：直接查询 \(sum\) 数组即可。

3. 整块对整块：查询 \(c_{i - 1, i, lsh_{i,Y_2}} - c_{L, i, lsh_{i, Y_1 - 1}}\) 和 \(c_{i - 1, i, lsh_{i, Y_1}} - c_{L, i, lsh_{i, Y_1 - 1}}\) ，此时只需要再查询 \([L + 1, i]\) 内 \(< Y_1\) 点的个数， \(i\) 块内 \([Y_1, Y_2]\) 点的个数。

4. 散块对整块：暴力枚举散块内的点，用 \(p\) 查询。

5. 散块对散块：暴力枚举散块内的点，用 \(p\) 查询，或直接归并。

[Ynoi2016] 镜中的昆虫

题目描述

您正在欣赏 galgame 的 HS，然后游戏崩溃了，于是您只能做数据结构题了：

维护一个长为 \(n\) 的序列 \(a_i\)，有 \(m\) 次操作。

1. 将区间 \([l,r]\) 的值修改为 \(x\)。

2. 询问区间 \([l,r]\) 出现了多少种不同的数，也就是说同一个数出现多次只算一个。

题解

首先统计出所有出现过的颜色，考虑删去询问区间 \([l, r]\) 内不存在的颜色。

对于每个颜色，记录它在序列中出现的位置，设这些位置构成的数组为 \(pos\) ，对于 \(pos\) 中相邻元素 \(pos_i, pos_{i+1}\) ，容易发现满足条件 \(pos_i<l\le r<pos_{i+1}\) 的所有询问不包含该颜色。

如果不考虑修改操作，我们以 \(l\) 为 \(x\) 轴，以 \(r\) 为 \(y\) 轴，题目可以转化为：

在一个二维平面上进行两种操作：

1.给所有满足 \(pos_i<x<pos_{i+1}, pos_i<y<pos_{i+1}\) 的点 \((x, y)\) 加 \(1\) ；

2.单点查询 \((x, y)\) 的权值。

考虑修改操作，由于修改中区间颜色相同，很容易想到珂朵莉树，因此每个颜色的 \(pos\) 数组不再维护位置，而是维护一段连续的区间 \([l, r]\) ，考虑两个相邻的区间 \([l_i, r_i], [l_{i+1}, r_{i+1}]\) ，容样发现所有满足 \(r_i<l\le r<l_{i+1}\) 的询问不存在这种颜色。

因此使用珂朵莉树维护整个序列，每次暴力删除插入一整段区间，容易发现删除和插入的次数是 \(O(n)\) 的，仍能转化为上述二维平面。

上述二维平面实际是一个三维偏序，用 \(cdq\) 分治解决时间维，用扫描线解决 \(x\) ，用树状数组解决 \(y\) 即可。