图论
图论
圆方树
点双连通分量
定义:图中任意两不同点之间都有至少两条点不重复的路径。
点不重复既指路径上点不重复(简单路径),也指两条路径的交集为空(当然,路径必然都经过出发点和到达点,这不在考虑范围内)。
暂不考虑点数为 \(1\) 的图。
一个近乎等价的定义是:不存在割点的图。
这个定义只在图中只有两个点,一条连接它们的边时失效。它没有割点,但是并不能找到两条不相交的路径,因为只有一条路径。
(也可以理解为那一条路径可以算两次,的确没有交,因为除起点和终点外路径中包含的点为空集)
而一个图的点双连通分量则是一个极大点双连通子图。
构造
与强连通分量等不同,一个点可能属于多个点双,但是一条边属于恰好一个点双。
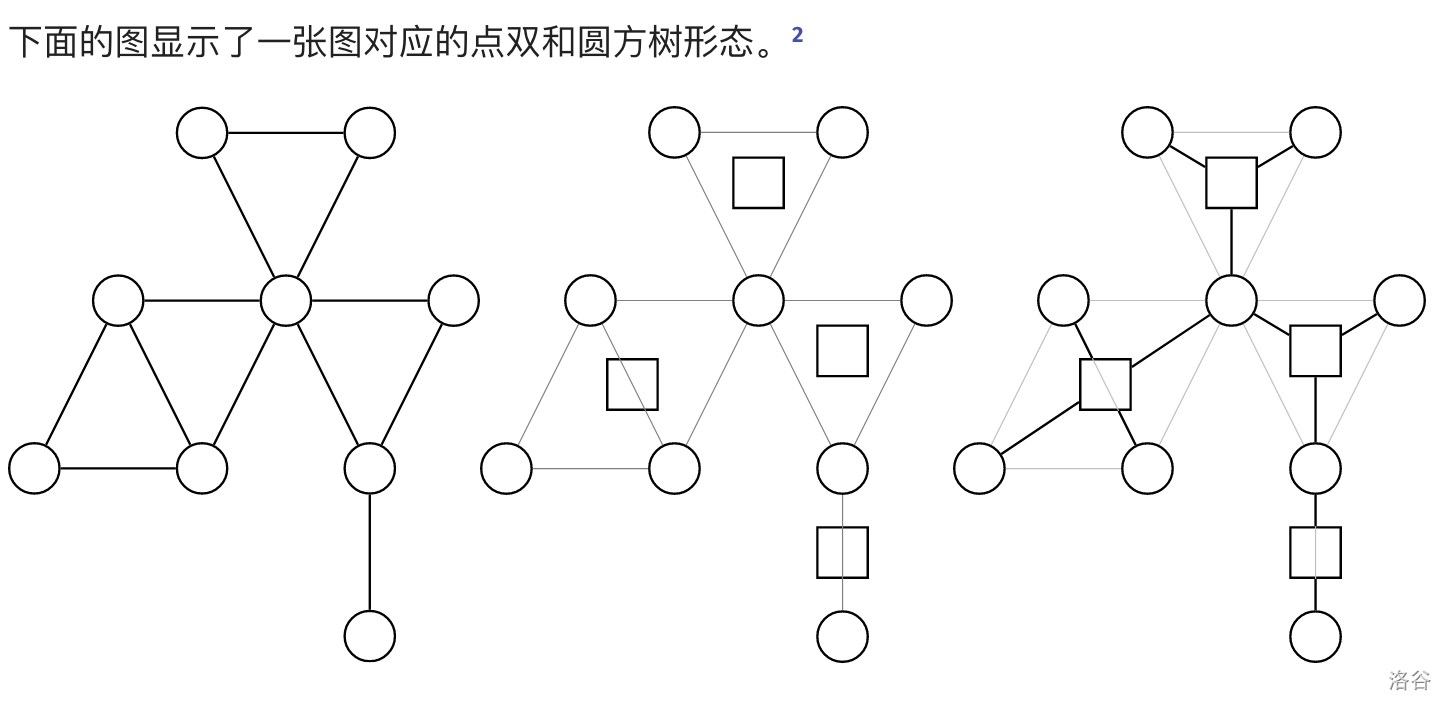
在圆方树中,原来的每个点对应一个圆点,每一个点双对应一个方点。
所以共有 \(n+c\) 个点,其中 \(n\) 是原图点数, \(c\) 是原图点双连通分量的个数。
而对于每一个点双连通分量,它对应的方点向这个点双连通分量中的每个点连边。
每个点双形成一个菊花图,多个菊花图通过原图中的割点连接在一起(因为点双的分隔点是割点)。
显然,圆方树中每条边连接一个圆点和一个方点。
代码实现
简单改造 Tarjan 算法求解点双即可。
void Tarjan ( int now )
{
dfn[now] = low[now] = ++dfs_clock;
s[++top] = now;
for ( auto v : edge[now] )
{
if ( !dfn[v] )
{
Tarjan(v);
low[now] = min(low[now], low[v]);
if ( low[v] == dfn[now] )
{
++matrix; int x;
do
{
x = s[top--];
new_edge[matrix].push_back(x);
} while ( x != v );
new_edge[now].push_back(matrix);
}
}
else
low[now] = min(low[now], dfn[v]);
}
return;
}
应用
APIO 2018 铁人两项
比特镇的路网由 \(m\) 条双向道路连接的 \(n\) 个交叉路口组成。
最近,比特镇获得了一场铁人两项锦标赛的主办权。这场比赛共有两段赛程:选手先完成一段长跑赛程,然后骑自行车完成第二段赛程。
比赛的路线要按照如下方法规划:
1.先选择三个两两互不相同的路口 \(s\) , \(c\) 和 \(f\) ,分别作为比赛的起点、切换点(运动员在长跑到达这个点后,骑自行车前往终点)、终点。
2.选择一条从 \(s\) 出发,经过 \(c\) 最终到达 \(f\) 的路径。考虑到安全因素,选择的路径经过同一个点至多一次。
在规划路径之前,镇长想请你帮忙计算,总共有多少种不同的选取 \(s\) , \(c\) 和 \(f\) 的方案,使得在第 2 步中至少能设计出一条满足要求的路径。
题解
选择的路径经过同一个点至多一次,不难想到点双连通分量。
假设三个点均在同一个点双连通分量,考虑这三个点是否能够合法。
想象使用 Tarjan 求解点双的过程,不妨从 \(c\) 开始 dfs ,此时出现的生成树以 \(c\) 为根节点连接树边,考虑构造路径,从 \(s\) 到 \(c\) 一直使用树边,从 \(f\) 到 \(c\) 先进入子树,然后通过返祖边到达 \(c\) ,在 \(c\) 处拼接路径。
利用上述性质求解答案,首先建立圆方树,首先枚举 \(c\) 点,然后考虑 \(s,f\) 点的位置,找到 \(c\) 与 \(s\) 路径上与 \(c\) 最近的圆点 \(p\) ,同理找到 \(f\) 与 \(c\) 路径上与 \(c\) 最近的圆点 \(q\) ,不难发现合法方案的充分必要条件为 \(p\ne q\) ( \(p=q\) 由于 \(p,q\) 为割点,路径一定重合)。
因此考虑枚举 \(c\) 和 \(p\) ,设连接 \(c, p\) 的方点为 \(x\) ,删除 \(x\) ,设 \(p\) 所在连通块中圆点个树为 \(siz\) ,删除前连痛块中圆点个数为 \(sum\) ,那么满足条件的 \(f\) 的个数为 \(sum-siz-1\) 。
简单优化后只需要枚举 \(p\) 和 \(x\) ,总贡献为 \((deg_x-1)\times (sum-size-1)\) 。
继续优化发现 \(p\) 和 \(x\) 路径上靠近 \(x\) 的圆点所在子树中所有圆点与 \(p\) 的贡献相同,简单合并统计即可。
#include <cstdio>
#include <vector>
using namespace std;
const int max1 = 1e5;
int n, m;
vector <int> edge[max1 + 5], new_edge[max1 * 2 + 5];
int dfn[max1 + 5], low[max1 + 5], dfs_clock;
int s[max1 + 5], top, matrix_cnt;
int sum[max1 * 2 + 5];
bool vis[max1 * 2 + 5];
long long ans;
void Tarjan ( int now )
{
dfn[now] = low[now] = ++dfs_clock;
s[++top] = now;
for ( int v : edge[now] )
{
if ( !dfn[v] )
{
Tarjan(v);
low[now] = min(low[now], low[v]);
if ( low[v] == dfn[now] )
{
++matrix_cnt;
do
{
new_edge[matrix_cnt].push_back(s[top]);
new_edge[s[top]].push_back(matrix_cnt);
top--;
} while ( s[top + 1] != v );
new_edge[matrix_cnt].push_back(now);
new_edge[now].push_back(matrix_cnt);
}
}
else
low[now] = min(low[now], dfn[v]);
}
return;
}
void Get_Size ( int now )
{
vis[now] = true;
sum[now] = now <= n;
for ( auto v : new_edge[now] )
{
if ( vis[v] )
continue;
Get_Size(v);
sum[now] += sum[v];
}
return;
}
void Dfs ( int now, int fa, int root )
{
for ( auto v : new_edge[now] )
{
if ( v == fa )
continue;
Dfs(v, now, root);
}
if ( now > n )
{
int deg = new_edge[now].size();
for ( auto v : new_edge[now] )
{
if ( v == fa )
continue;
ans += 1LL * sum[v] * (sum[root] - sum[v] - 1) * (deg - 1);
}
int s = sum[root] - sum[now];
ans += 1LL * s * (sum[root] - s - 1) * (deg - 1);
}
return;
}
int main ()
{
scanf("%d%d", &n, &m);
for ( int i = 1, u, v; i <= m; i ++ )
{
scanf("%d%d", &u, &v);
edge[u].push_back(v);
edge[v].push_back(u);
}
matrix_cnt = n;
for ( int i = 1; i <= n; i ++ )
if ( !dfn[i] )
Tarjan(i);
for ( int i = 1; i <= matrix_cnt; i ++ )
{
if ( !vis[i] )
{
Get_Size(i);
Dfs(i, 0, i);
}
}
printf("%lld\n", ans);
return 0;
}
CF487E Tourists
Cyberland 有 \(n\) 座城市,编号从 \(1\) 到 \(n\),有 \(m\) 条双向道路连接这些城市。第 \(j\) 条路连接城市 \(a_j\) 和 \(b_j\)。每天,都有成千上万的游客来到 Cyberland 游玩。
在每一个城市,都有纪念品售卖,第 \(i\) 个城市售价为 \(w_i\)。这个售价有时会变动。
每一个游客的游览路径都有固定起始城市和终止城市,且不会经过重复的城市。
他们会在路径上的城市中,售价最低的那个城市购买纪念品。
你能求出每一个游客在所有合法的路径中能购买的最低售价是多少吗?
你要处理 \(q\) 个操作:
C a w: 表示 \(a\) 城市的纪念品售价变成 \(w\)。
A a b: 表示有一个游客要从 \(a\) 城市到 \(b\) 城市,你要回答在所有他的旅行路径中最低售价的最低可能值。
题解
圆方树 + 树剖。
[SDOI2018] 战略游戏
省选临近,放飞自我的小 Q 无心刷题,于是怂恿小 C 和他一起颓废,玩起了一款战略游戏。
这款战略游戏的地图由 \(n\) 个城市以及 \(m\) 条连接这些城市的双向道路构成,并且从任意一个城市出发总能沿着道路走到任意其他城市。
现在小 C 已经占领了其中至少两个城市,小 Q 可以摧毁一个小 C 没占领的城市,同时摧毁所有连接这个城市的道路。只要在摧毁这个城市之后能够找到某两个小 C 占领的城市 \(u\) 和 \(v\),使得从 \(u\) 出发沿着道路无论如何都不能走到 \(v\),那么小 Q 就能赢下这一局游戏。
小 Q 和小 C 一共进行了 \(q\) 局游戏,每一局游戏会给出小 C 占领的城市集合 \(S\),你需要帮小 Q 数出有多少个城市在他摧毁之后能够让他赢下这一局游戏。
题解
圆方树 + 虚树。
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
const int max1 = 1e5, max2 = 20;
int T, n, m, q;
vector <int> edge[max1 + 5];
int dfn[max1 * 2 + 5], low[max1 + 5], dfs_clock;
int s[max1 * 2 + 5], top;
vector <int> new_edge[max1 * 2 + 5];
int matrix_cnt;
int siz, qus[max1 + 5], ans;
int deep[max1 * 2 + 5], father[max1 * 2 + 5][max2 + 2];
int val[max1 * 2 + 5];
void Clear ()
{
for ( int i = 1; i <= n; i ++ )
edge[i].clear();
memset(dfn, 0, sizeof(int) * (n + 2));
dfs_clock = top = 0;
for ( int i = 1; i <= n + n; i ++ )
new_edge[i].clear();
matrix_cnt = n;
return;
}
void Tarjan ( int now )
{
dfn[now] = low[now] = ++dfs_clock;
s[++top] = now;
for ( auto v : edge[now] )
{
if ( !dfn[v] )
{
Tarjan(v);
low[now] = min(low[now], low[v]);
if ( low[v] == dfn[now] )
{
++matrix_cnt;
do
{
new_edge[matrix_cnt].push_back(s[top]);
new_edge[s[top]].push_back(matrix_cnt);
--top;
} while ( s[top + 1] != v );
new_edge[matrix_cnt].push_back(now);
new_edge[now].push_back(matrix_cnt);
}
}
else
low[now] = min(low[now], dfn[v]);
}
return;
}
void Dfs ( int now, int fa )
{
dfn[now] = ++dfs_clock;
deep[now] = deep[fa] + 1;
father[now][0] = fa;
val[now] = val[fa] + (now <= n);
for ( int i = 1; (1 << i) <= deep[now]; i ++ )
father[now][i] = father[father[now][i - 1]][i - 1];
for ( auto v : new_edge[now] )
{
if ( v == fa )
continue;
Dfs(v, now);
}
return;
}
int Lca ( int u, int v )
{
if ( deep[u] < deep[v] )
swap(u, v);
for ( int i = max2; i >= 0; i -- )
if ( (1 << i) <= deep[u] - deep[v] )
u = father[u][i];
if ( u == v )
return u;
for ( int i = max2; i >= 0; i -- )
if ( (1 << i) <= deep[u] && father[u][i] != father[v][i] )
u = father[u][i], v = father[v][i];
return father[u][0];
}
bool Cmp ( const int &x, const int &y )
{
return dfn[x] < dfn[y];
}
void Insert ( int x )
{
if ( !top )
{
ans += x <= n;
s[++top] = x;
}
else
{
int lca = Lca(s[top], x);
if ( lca == s[top] )
{
ans += val[x] - val[lca];
s[++top] = x;
}
else
{
ans += val[s[top]] - val[lca];
ans += val[x] - val[lca];
ans += (lca <= n);
while ( top > 1 && deep[s[top - 1]] > deep[lca] )
{
ans -= val[s[top]] - val[s[top - 1]];
--top;
}
if ( top == 1 )
{
ans -= (s[top] <= n);
--top;
}
else
{
ans -= val[s[top]] - val[lca];
ans -= (lca <= n);
--top;
}
s[++top] = lca;
s[++top] = x;
}
}
return;
}
void Solve ()
{
ans = 0;
sort(qus + 1, qus + 1 + siz, Cmp);
top = 0;
for ( int i = 1; i <= siz; i ++ )
Insert(qus[i]);
printf("%d\n", ans - siz);
return;
}
void Work ()
{
scanf("%d%d", &n, &m);
Clear();
for ( int i = 1, u, v; i <= m; i ++ )
{
scanf("%d%d", &u, &v);
edge[u].push_back(v);
edge[v].push_back(u);
}
Tarjan(1);
dfs_clock = 0;
deep[0] = 0;
memset(father[0], 0, sizeof(father[0]));
val[0] = 0;
Dfs(1, 0);
scanf("%d", &q);
while ( q -- )
{
scanf("%d", &siz);
for ( int i = 1; i <= siz; i ++ )
scanf("%d", &qus[i]);
Solve();
}
return;
}
int main ()
{
scanf("%d", &T);
while ( T -- )
Work();
return 0;
}
2-SAT
定义
SAT 是适定性(Satisfiability)问题的简称。一般形式为 k - 适定性问题,简称 k-SAT。而当 \(k>2\) 时该问题为 NP 完全的。所以我们只研究 \(k=2\) 的情况。
2-SAT,简单的说就是给出 \(n\) 个集合,每个集合有两个元素,已知若干个 \(\langle a,b \rangle\) ,表示 \(a\) 与 \(b\) 矛盾(其中 \(a\) 与 \(b\) 属于不同的集合)。然后从每个集合选择一个元素,判断能否一共选 \(n\) 个两两不矛盾的元素。显然可能有多种选择方案,一般题中只需要求出一种即可。
建图
\(n\) 对夫妇出席宴会,一对夫妇中至少有一个人出席宴会,定义 \(a_i\) 表示第 \(i\) 对夫妇中的女士, \(b_i\) 表示第 \(i\) 对夫妇中的先生,存在 \(m\) 对矛盾关系,例如 \(<a_i, b_j>\) 表示第 \(i\) 个女士与第 \(j\) 个先生有矛盾。
可以发现选择了 \(a_i\) 必须选择 \(a_j\) ,从 \(a_i\) 向 \(a_j\) 连接有向边,选择了 \(b_j\) 必须选择 \(b_i\) ,从 \(b_j\) 向 \(b_i\) 连接有向边。
容易发现 \(a_i, b_i\) 在同一个强连通分量中,不存在合法方案。
否则一定存在合法方案。(详细证明:https://wenku.baidu.com/view/31fd7200bed5b9f3f90f1ce2.html?wkts=1721284300133)
考虑构造合法方案,对强连通分量构成的 DAG 进行拓扑排序,对于一组 \(a_i, b_i\) ,选择其中拓扑序较大的点,这样选择造成的限制较小。
实际上 Tarjan 算法中的入栈序便是反向的拓扑序。
应用
[NEERC2016] Binary Code
给定 n 个01串,每个字符串至多有一位是未知的,可以填 0 或 1 ,求是否存在一种方案,使得任意一个字符串不是其它任意一个字符串的前缀。
题解
每个串有两种情况,不难想到 2-SAT 。
考虑两个长度不同的串 \(s, t\) ,如果 \(s\) 是 \(t\) 的前缀,那么 \(s\) 向 \(t\) 的 否定 建边,同时 \(t\) 向 \(s\) 的 否定 建边。
暴力建边复杂度为 \(O(n^2)\) ,使用 01Trie 优化。
对于一个串 \(s\) ,找到 \(s\) 在 Trie 上的节点 \(now\) ,发现 \(s\) 需要向其祖先节点对应的所有串的否定建边,需要向其子树内节点对应的所有串的否定建边。
因此建立一棵根向树,一棵叶向树,两棵树的节点分别向其包含的串的否定建边,对于串 \(s\) ,建立到根向树对应节点的父亲的边和到叶向树对应节点的儿子的边即可。
对于长度相同的串 \(s, t\) ,若 \(s=t\) ,同样需要 \(s\) 向 \(t\) 的 否定 建边, \(t\) 向 \(s\) 的 否定 建边。
因此对于 Trie 上一个节点对应的所有串,其中任意一个串需要向其他串的 否定 连边,前缀和优化建图即可。
若出现没有 ? 的串,可以任选一位,然后强制其为 0/1 。
#include <bits/stdc++.h>
using namespace std;
const int MAX = 5e5;
#define ops(now) ( ( now & 1 ) ? ( now + 1 ) : ( now - 1 ) )
int n,pos[MAX + 5],location[MAX + 5][2],point_cnt;
string s[MAX + 5];
struct Graph
{
struct Node{int next,v;}edge[MAX * 20 + 5];
int head[MAX * 10 + 5],total;
int low[MAX * 10 + 5],dfn[MAX * 10 + 5],dfs_clock,belong[MAX * 10 + 5],cnt;
bool in[MAX * 10 + 5];
stack <int> sta;
Graph()
{
memset(head,0,sizeof(head));
memset(low,0,sizeof(low));
total = dfs_clock = cnt = 0;
}
inline void Add ( int u,int v )
{
edge[++total].v = v;
edge[total].next = head[u];
head[u] = total;
return;
}
void Tarjan ( int now )
{
dfn[now] = low[now] = ++ dfs_clock;
in[now] = true;
sta.push(now);
for ( int i = head[now];i;i = edge[i].next )
{
if ( !dfn[edge[i].v] )
{
Tarjan(edge[i].v);
low[now] = min(low[now],low[edge[i].v]);
}
else if ( in[edge[i].v] )
{
low[now] = min(low[now],dfn[edge[i].v]);
}
}
if ( dfn[now] == low[now] )
{
int x;
cnt ++;
do
{
x = sta.top();
in[x] = false;
belong[x] = cnt;
sta.pop();
}while ( x != now );
}
return;
}
inline void Tarjan ()
{
for ( int i = 1;i <= point_cnt;i ++ ) if ( !dfn[i] ) Tarjan(i);
for ( int i = 1;i <= n;i ++ )
{
if ( belong[( i << 1 ) - 1] == belong[i << 1] )
{
puts("NO");
return;
}
}
puts("YES");
return;
}
}G;
struct Trie
{
#define lson(now) tree[now].son[0]
#define rson(now) tree[now].son[1]
#define fa(now) tree[now].father
struct Struct_Trie
{
int son[2],father;
vector <int> num;
}tree[MAX * 2 + 5];
int total;
Trie(){total = 1;lson(1) = rson(1) = fa(1) = 0;}
inline int Insert ( const string &st,const int &id )
{
int len = st.length(),now = 1;
for ( int i = 0;i < len;i ++ )
{
if ( st[i] == '0' )
{
if ( !lson(now) )
{
lson(now) = ++ total;
fa(total) = now;
lson(total) = rson(total) = 0;
}
now = lson(now);
}
else if ( st[i] == '1' )
{
if ( !rson(now) )
{
rson(now) = ++ total;
fa(total) = now;
lson(total) = rson(total) = 0;
}
now = rson(now);
}
}
tree[now].num.push_back(id);
return now;
}
inline void Build ()
{
for ( int i = 1;i <= total;i ++ ) if ( fa(i) ) G.Add(i + point_cnt,fa(i) + point_cnt);
for ( int i = 1;i <= n;i ++ )
{
int x;
if ( location[i][0] )
{
x = location[i][0];
G.Add(x + point_cnt,i << 1);
if ( fa(x) ) G.Add(( i << 1 ) - 1,fa(x) + point_cnt);
}
if ( location[i][1] )
{
x = location[i][1];
G.Add(x + point_cnt,( i << 1 ) - 1);
if ( fa(x) ) G.Add(i << 1,fa(x) + point_cnt);
}
}
point_cnt += total;
for ( int i = 1;i <= total;i ++ ) if ( fa(i) ) G.Add(fa(i) + point_cnt,i + point_cnt);
for ( int i = 1;i <= n;i ++ )
{
int x;
if ( location[i][0] )
{
x = location[i][0];
G.Add(( i << 1 ) - 1,x + point_cnt);
if ( fa(x) ) G.Add(fa(x) + point_cnt,i << 1);
}
if ( location[i][1] )
{
x = location[i][1];
G.Add(i << 1,x + point_cnt);
if ( fa(x) ) G.Add(fa(x) + point_cnt,( i << 1 ) - 1);
}
}
point_cnt += total;
for ( int i = 1;i <= total;i ++ )
{
int len = tree[i].num.size();
if ( len >= 2 )
{
for ( int j = 1;j <= len;j ++ )
{
G.Add(tree[i].num[j - 1],j + point_cnt);
G.Add(j + len + point_cnt,ops(tree[i].num[j - 1]));
}
for ( int j = 1;j < len;j ++ )
{
G.Add(j + point_cnt,j + 1 + point_cnt);
G.Add(j + point_cnt,ops(tree[i].num[j]));
G.Add(tree[i].num[j],j + len + point_cnt);
G.Add(j + 1 + len + point_cnt,j + len + point_cnt);
}
point_cnt += len << 1;
}
}
}
}Tree;
int main()
{
cin >> n;
for ( int i = 1;i <= n;i ++ )
{
cin >> s[i];
int len = s[i].length();
pos[i] = -1;
for ( int j = 0;j < len;j ++ ) if ( s[i][j] == '?' ) pos[i] = j;
int x = ( i << 1 ) - 1,y = ( i << 1 );
if ( !~pos[i] )
{
pos[i] = 0;
if ( s[i][0] == '0' )
{
G.Add(y,x);
location[i][0] = Tree.Insert(s[i],x);
}
else if ( s[i][0] == '1' )
{
G.Add(x,y);
location[i][1] = Tree.Insert(s[i],y);
}
}
else if ( ~pos[i] )
{
s[i][pos[i]] = '0';
location[i][0] = Tree.Insert(s[i],x);
s[i][pos[i]] = '1';
location[i][1] = Tree.Insert(s[i],y);
}
}
point_cnt = n << 1;
Tree.Build();
G.Tarjan();
return 0;
}
[JSOI2019] 精准预测
目前,火星小镇上有\(n\)个居民(编号\(1,2,……,n\))。机器学习算法预测出这些居民在接下来\(T\)个时刻(编号\(1,2,……,T\))的生死情况,每条预测都是如下两种形式之一:
-
难兄难弟\(0\) \(t\) \(x\) \(y\):在\(t\)时刻,如果\(x\)是死亡状态,那么在\(t+1\)时刻,\(y\)是死亡状态。(注意,当\(x\)在\(t\)时刻是生存状态时,该预测也被认为是正确的);
-
死神来了\(1\) \(t\) \(x\) \(y\):在\(t\)时刻,如果\(x\)是生存状态,那么在\(t\)时刻,\(y\)是死亡状态。(注意,当\(x\)在\(t\)时刻是死亡状态时,该预测也被认为是正确的)。
注意本题是对某个时刻进行生死状态的预测,如果某个人在\(t\)时刻是生存状态,在\(t+1\)时刻是死亡状态,你可以认为是在\(t\)到\(t+1\)这段时间内发生了某个事件导致其死亡。
虽然 JYY 对自己从大数据中统计得到的模型非常自信,但火星人看到这些预测吓了一跳,表示实在难以接受这种设定,更是认为计算机科学是可怕的邪教,打破了他们平静的生活。为了安抚火星人的情绪, JYY 打算从这些预测结果中推导出一些火星人更容易接受的事实,从而安抚火星人的情绪。
具体来说,JYY 首先假设对火星人生死的预测全部正确,在此基础上,JYY 希望为小镇上的每个居民\(k\)分别计算有多少个火星人有可能和他一起活到第\(T+1\)时刻,换言之,JYY 希望为每个火星人\(k\)计算
其中 \(\operatorname{Live}(i,j)=1\) 表示编号为\(i\)和\(j\)的火星人有可能同时在第 \(T+1\) 时刻处于生还状态,否则\(\operatorname{Live}(i,j)=0\)。
注意火星人是不能够复活的。一个火星人可能在时刻\(1\)就处于死亡状态,也有可能有预测未覆盖的死亡情况发生(火星人在任何时候都可能死亡,但任意时刻观察到火星人的状态要么活着,要么死亡)。最后,注意到\(\operatorname{Live}\)是为每一对火星人分别独立计算的,因此\(\operatorname{Live}(x,y)=1,\operatorname{Live}(y,z)=1\)并不意味着\(\operatorname{Live}(x,z)=1\)。
对于 \(100\%\) 的数据, \(T\le 10^6, n\le 5\times 10^4, m\le 10^5\) 。
题解
比较显然的思路是把每一对 \((x, t)\) 当作一个点,表示 \(x\) 在 \(t\) 时刻仍然活着,类似的每一对 \(\neg(x, t)\) 也是一个点,表示 \(x\) 在 \(t\) 时刻死亡。
这与 2-SAT 的建图方式极为相像,因此用 2-SAT 的方法建边。
如果 \(x\) 在 \(t\) 时刻仍然活着,那么 \(x\) 在 \(t-1\) 时刻一定也活着,建边 \((x, t)\to (x, t - 1)\) 。
如果 \(x\) 在 \(t-1\) 时刻处于死亡,那么 \(x\) 在 \(t\) 时刻一定也处于死亡,建边 \(\neg(x, t - 1)\to\neg(x, t)\) 。
难兄难弟:
如果 \(x\) 在 \(t\) 时刻处于死亡状态, \(y\) 在 \(t+1\) 时刻处于死亡状态,建边 \(\neg(x, t)\to\neg(y, t + 1)\) 。
如果 \(y\) 在 \(t + 1\) 时刻活着, \(x\) 在 \(t\) 时刻也活着,建边 \((y, t + 1)\to (x, t)\) 。
死神来了:
如果 \(x\) 在 \(t\) 时刻处于生存状态, \(y\) 在 \(t\) 时刻处于死亡状态,建边 \((x, t)\to\neg(y, t)\) 。
如果 \(y\) 在 \(t\) 时刻处于生存状态, \(x\) 在 \(t\) 时刻处于死亡状态,建边 \((y, t)\to\neg(x, t)\) 。
考虑判断在 \(T + 1\) 时刻, \(x\) 活着的时候 \(y\) 能否活着。
由于我们所建图表示一种推理关系,一个有向边 \((u, v)\) 表示 \(u\) 能够推理出 \(v\) ,因此我们从 \((x, T + 1)\) 开始推理,如果存在一条到达 \(\neg(y, T + 1)\) 的路径,那么 \(y\) 一定死亡。
因此得到一个 \(O(n^2)\) 的做法。
优化非常暴力,用 bitset 维护 \(f_{x, t}\) 表示 \((x, t)\) 可以到达的所有 \((x, T + 1)\) 构成的集合,转移相当于在 DAG 上 dp 。
#include <cstdio>
#include <map>
#include <bitset>
#include <queue>
#include <iostream>
using namespace std;
const int max1 = 5e4, max2 = 1e5, B = 1e4;
int T, n, m;
map <int, int > Map[max1 + 5];
pair <int, int> point[max1 * 4 + max2 * 4 + 5];
int deg[max1 * 4 + max2 * 4 + 5], total;
vector <int> edge[max1 * 4 + max2 * 4 + 5];
queue <int> que;
int seq[max1 * 4 + max2 * 4 + 5], cnt;
bitset <B + 5> vis[max1 * 4 + max2 * 4 + 5], tmp;
int ans[max1 + 5];
bool illegal[max1 + 5];
int Insert ( int x, int t )
{
if ( Map[x].find(t) == Map[x].end() )
{
Map[x][t] = ++total;
point[total] = make_pair(x, t);
++total;
}
return Map[x][t];
}
void Solve ( int L, int R )
{
for ( int i = 1; i <= total; i ++ )
vis[i].reset();
for ( int i = 1; i <= total; i ++ )
{
int now = seq[i];
if ( !(now & 1) && point[now - 1].second == T + 1 && point[now - 1].first >= L && point[now - 1].first <= R )
vis[now].set(point[now - 1].first - L);
for ( auto v : edge[now] )
vis[v] |= vis[now];
}
tmp.reset();
for ( int i = 1; i <= total; i ++ )
{
int now = seq[i];
if ( (now & 1) && point[now].second == T + 1 )
{
if ( point[now].first >= L && point[now].first <= R && vis[now].test(point[now].first - L) )
{
illegal[point[now].first] = true;
tmp.set(point[now].first - L);
}
}
}
for ( int i = 1; i <= total; i ++ )
{
int now = seq[i];
if ( (now & 1) && point[now].second == T + 1 )
ans[point[now].first] += (vis[now] | tmp).count();
}
return;
}
int main ()
{
int opt, tim, x, y;
scanf("%d%d%d", &T, &n, &m);
for ( int i = 1; i <= m; i ++ )
{
scanf("%d%d%d%d", &opt, &tim, &x, &y);
if ( !opt )
{
int A = Insert(x, tim), B = Insert(y, tim + 1);
edge[B + 1].push_back(A + 1); ++deg[A + 1];
edge[A].push_back(B); ++deg[B];
}
else
{
int A = Insert(x, tim), B = Insert(y, tim);
edge[B + 1].push_back(A); ++deg[A];
edge[A + 1].push_back(B); ++deg[B];
}
}
for ( int i = 1; i <= n; i ++ )
{
int pre = Insert(i, 0);
for ( auto v : Map[i] )
{
if ( v.first )
{
edge[v.second + 1].push_back(pre + 1); ++deg[pre + 1];
edge[pre].push_back(v.second); ++deg[v.second];
pre = v.second;
}
}
if ( point[pre].second != T + 1 )
{
int now = Insert(i, T + 1);
edge[now + 1].push_back(pre + 1); ++deg[pre + 1];
edge[pre].push_back(now); ++deg[now];
}
}
for ( int i = 1; i <= total; i ++ )
if ( !deg[i] )
que.push(i);
while ( !que.empty() )
{
int now = que.front();
que.pop();
seq[++cnt] = now;
for ( auto v : edge[now] )
{
--deg[v];
if ( !deg[v] )
que.push(v);
}
}
int L = 1, R = min(B, n);
while ( true )
{
if ( L > n )
break;
Solve(L, R);
L = R + 1;
R = min(n, L + B - 1);
}
for ( int i = 1; i <= n; i ++ )
{
if ( illegal[i] )
printf("0 ");
else
printf("%d ", n - 1 - ans[i]);
}
printf("\n");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号