2023冲刺清北营6
所以龙族是本小说吗?
T1 万家灯火
首先考虑暴力,假设当前的询问为 \(x,d\) ,实际上我们需要计数以 \(x\) 为根时与 \(x\) 距离不超过 \(d\) 的满足 \(color_u=1,color_{fa_u}=0\) 的点的数量。
考虑用点分树优化,设查询为 \(x,d\) ,当前分治中心为 \(u\) ,我们需要统计跨过 \(u\) 的与 \(x\) 距离不超过 \(d\) 的点的数量,设上一次经过的分治中心为 \(pre\) ,实际上我们统计的是以 \(u\) 为根的点分树内距离 \(u\) 不超过 \(d-\operatorname{dis}(u,x)\) 的点的数量,减去 \(pre\) 这个儿子对此产生的贡献。
很容易产生一个想法是对于每个分治中心维护一棵树状数组,下标为点的深度,这样我们很容易在 \(O(\log n)\) 的时间复杂度内进行查询,考虑修改操作,设修改的点为 \(x\) ,当前遍历到的分治中心为 \(u\) ,只需要对于每个分治中心,以及这个分治中心下的每个点维护儿子中 \(color_v=1\) 的数量就可以很容易对树状数组进行修改。考虑一种特殊的情况,如果 \(x\) 为当前遍历的分治中心,考虑到答案需要进行容斥计算,因此需要维护对每个分治中心以及分治中心下的儿子维护树状数组,然而暴力遍历 \(x\) 的所有儿子复杂度显然不正确,因此不如考虑特殊处理这部分的答案。具体的,在每个分治中心维护树状数组表示以当前分治中心为根的整颗子树中满足条件的点的数量,钦定分治中心 \(color=1\) 进行维护(不管分治中心的真实颜色),显然这样可以保证修改的复杂度。考虑查询,实际上只需要加入分治中心颜色为 \(0\) 时产生的新贡献即可,这很容易使用之前维护的每个点颜色为 \(1\) 的儿子的数量进行计算,之后加入分治中心产生的贡献即可。
code
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int max1 = 1e5, max_lg = 17;
int n, q;
vector <int> edge[max1 + 5];
char color[max1 + 5];
bool vis[max1 + 5];
int siz[max1 + 5], maxdeep[max1 + 5], root;
struct Bit
{
#define lowbit(now) ( now & -now )
int lim;
vector <int> tree;
void Resize ( int __lim )
{
lim = __lim;
tree.resize(__lim + 1);
for ( int i = 0; i <= __lim; i ++ )
tree[i] = 0;
return;
}
void Insert ( int now, int x )
{
if ( x )
{
while ( now <= lim )
{
tree[now] += x;
now += lowbit(now);
}
}
return;
}
int Query ( int now )
{
if ( now < 0 )
return 0;
now = min(now, lim);
int res = 0;
while ( now )
{
res += tree[now];
now -= lowbit(now);
}
return res;
}
}Tree1[max1 + 5], Tree2[max1 + 5];
int point[max1 + 5], b[max1 + 5], top[max1 + 5];
int bin[max_lg + 5][max1 + 5], father[max_lg + 5][max1 + 5], deep[max_lg + 5][max1 + 5];
void Get_Size ( int now, int fa )
{
siz[now] = 1;
for ( auto v : edge[now] )
{
if ( vis[v] || v == fa )
continue;
Get_Size(v, now);
siz[now] += siz[v];
}
return;
}
void Get_Root ( int now, int fa, int sum )
{
bool is_root = true;
for ( auto v : edge[now] )
{
if ( vis[v] || v == fa )
continue;
Get_Root(v, now, sum);
if ( siz[v] > sum >> 1 )
is_root = false;
}
if ( sum - siz[now] > sum >> 1 )
is_root = false;
if ( is_root )
root = now;
return;
}
void Get_Deep ( int now, int fa )
{
maxdeep[now] = 1;
for ( auto v : edge[now] )
{
if ( vis[v] || v == fa )
continue;
Get_Deep(v, now);
maxdeep[now] = max(maxdeep[now], maxdeep[v] + 1);
}
return;
}
void Update ( int now, int fa, int depth, int x, int y, int bit )
{
if ( color[now] == '1' )
++bin[bit][fa];
father[bit][now] = fa;
deep[bit][now] = depth;
if ( fa != x && color[now] == '1' && color[fa] == '0' )
{
Tree1[x].Insert(depth, 1);
Tree2[y].Insert(depth, 1);
}
for ( auto v : edge[now] )
{
if ( vis[v] || v == fa )
continue;
Update(v, now, depth + 1, x, y, bit);
}
return;
}
void Build ( int now, int bit )
{
vis[now] = true;
b[now] = bit;
Get_Deep(now, 0);
Tree1[now].Resize(maxdeep[now]);
for ( auto v : edge[now] )
{
if ( vis[v] )
continue;
Get_Size(v, now);
Get_Root(v, now, siz[v]);
Tree2[root].Resize(maxdeep[now]);
Update(v, now, 1, now, root, bit);
}
for ( auto v : edge[now] )
{
if ( vis[v] )
continue;
Get_Size(v, now);
Get_Root(v, now, siz[v]);
point[root] = v;
top[root] = now;
Build(root, bit + 1);
}
return;
}
void Change ( int x )
{
if ( color[x] == '1' )
{
int pre = x, u = top[x];
while ( u )
{
int fa = father[b[u]][x];
if ( fa != u && color[fa] == '0' )
{
Tree1[u].Insert(deep[b[u]][x], -1);
Tree2[pre].Insert(deep[b[u]][x], -1);
}
Tree1[u].Insert(deep[b[u]][x] + 1, bin[b[u]][x]);
Tree2[pre].Insert(deep[b[u]][x] + 1, bin[b[u]][x]);
--bin[b[u]][fa];
pre = u;
u = top[u];
}
color[x] = '0';
}
else
{
int pre = x, u = top[x];
while ( u )
{
int fa = father[b[u]][x];
if ( fa != u && color[fa] == '0' )
{
Tree1[u].Insert(deep[b[u]][x], 1);
Tree2[pre].Insert(deep[b[u]][x], 1);
}
Tree1[u].Insert(deep[b[u]][x] + 1, -bin[b[u]][x]);
Tree2[pre].Insert(deep[b[u]][x] + 1, -bin[b[u]][x]);
++bin[b[u]][fa];
pre = u;
u = top[u];
}
color[x] = '1';
}
return;
}
int Query ( int x, int d )
{
int ans = 0;
if ( color[x] == '1' )
{
Change(x);
int u = top[x], pre = x;
ans = Tree1[x].Query(d);
if ( d )
ans += bin[b[x]][x];
while ( u )
{
int v = point[pre], dis = deep[b[u]][x];
ans += Tree1[u].Query(d - dis);
ans -= Tree2[pre].Query(d - dis);
if ( color[u] == '0' && dis + 1 <= d )
{
ans += bin[b[u]][u];
if ( color[v] == '1' )
--ans;
}
if ( dis <= d && color[u] == '1' && color[v] == '0' )
++ans;
pre = u;
u = top[u];
}
Change(x);
}
else
{
int u = top[x], pre = x;
ans = Tree1[x].Query(d);
if ( d )
ans += bin[b[x]][x];
while ( u )
{
int v = point[pre], dis = deep[b[u]][x];
ans += Tree1[u].Query(d - dis);
ans -= Tree2[pre].Query(d - dis);
if ( color[u] == '0' && dis + 1 <= d )
{
ans += bin[b[u]][u];
if ( color[v] == '1' )
--ans;
}
if ( dis <= d && color[u] == '1' && color[v] == '0' )
++ans;
pre = u;
u = top[u];
}
}
return ans;
}
int main ()
{
freopen("lights.in", "r", stdin);
freopen("lights.out", "w", stdout);
scanf("%d%d", &n, &q);
for ( int i = 2, u, v; i <= n; i ++ )
{
scanf("%d%d", &u, &v);
edge[u].push_back(v);
edge[v].push_back(u);
}
scanf("%s", color + 1);
Get_Size(1, 0);
Get_Root(1, 0, siz[1]);
Build(root, 0);
int opt, x, d;
while ( q -- )
{
scanf("%d%d", &opt, &x);
if ( opt == 1 )
Change(x);
else
scanf("%d", &d), printf("%d\n", Query(x, d));
}
return 0;
}
T2 逃亡
很容易将期望转化为一个点被访问过的概率的和,首先考虑 \(m=1\) 的情况。
设 \(P(i)\) 表示恰好 \(n\) 步从 \(0\) 走到 \(i\) 的概率,设 \(x\) 为向正方向运动的次数, \(y\) 为向负方向运动的次数,存在关系 \(x+y=n,x-y=i\) ,很容易解得 \(x=\tfrac{n+i}{2}\) ,因此有:
考虑求解 \(n\) 步内经过点 \(i\) 的概率,考虑第 \(n\) 步所处的位置 \(j\) ,如果 \(j=i\) ,显然贡献为 \(P(i)\) ,如果 \(j>i\) ,显然到达 \(j\) 的过程中一定经过 \(i\) ,因此贡献为 \(P(j)\) ,如果 \(j<i\) ,考虑在第一次经过 \(i\) 后对所有运动状态取反,发现贡献为 \(P(2i-j)\) ,因此实际上 \(n\) 步内经过点 \(i\) 的概率为 \(P(i)+\sum_{j>i}2(P_j)\) 。
考虑 \(m\ne 1\) 的情况,实际上就是求解一个点不被任意人访问到的概率,很容易求解。
code
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int max1 = 20;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
int n, m, x[max1 + 5], ans;
vector <int> inv, fac, ifac, E;
void Add ( int &x, int y )
{
x = x + y;
if ( x >= mod )
x = x - mod;
return;
}
int C ( int n, int m )
{
if ( n < m || n < 0 || m < 0 )
return 0;
return 1LL * fac[n] * ifac[n - m] % mod * ifac[m] % mod;
}
int Quick_Power ( int base, int p )
{
int res = 1;
while ( p )
{
if ( p & 1 )
res = 1LL * res * base % mod;
p >>= 1;
base = 1LL * base * base % mod;
}
return res;
}
void Solve ( int pos )
{
int res = 1;
for ( int i = 1; i <= m; i ++ )
{
if ( pos < x[i] )
{
if ( x[i] - pos <= n )
res = 1LL * res * ( 1 - E[x[i] - pos] + mod ) % mod;
}
else if ( pos > x[i] )
{
if ( pos - x[i] <= n )
res = 1LL * res * ( 1 - E[pos - x[i]] + mod ) % mod;
}
else
res = 0;
}
ans = ( ans + 1 - res + mod ) % mod;
return;
}
int main ()
{
freopen("exodus.in", "r", stdin);
freopen("exodus.out", "w", stdout);
scanf("%d%d", &n, &m);
for ( int i = 1; i <= m; i ++ )
scanf("%d", &x[i]);
inv.resize(n + 1);
fac.resize(n + 1);
ifac.resize(n + 1);
E.resize(n + 1);
inv[1] = 1;
for ( int i = 2; i <= n; i ++ )
inv[i] = 1LL * ( mod - mod / i ) * inv[mod % i] % mod;
fac[0] = 1, ifac[0] = inv[1];
for ( int i = 1; i <= n; i ++ )
fac[i] = 1LL * fac[i - 1] * i % mod,
ifac[i] = 1LL * ifac[i - 1] * inv[i] % mod;
int P = Quick_Power(Quick_Power(2, n), mod - 2);
for ( int i = !( n & 1 ) + 1; i <= n; i += 2 )
E[i] = 1LL * C(n, n + i >> 1) * P % mod;
int sum = 0;
for ( int i = n; i >= 1; i -- )
{
Add(sum, E[i]);
E[i] = mod - E[i];
Add(E[i], sum);
Add(E[i], sum);
}
sort(x + 1, x + 1 + m);
x[0] = -inf;
for ( int i = 1; i <= m; i ++ )
for ( int k = max(x[i - 1] + n + 1, x[i] - n); k <= x[i] + n; k ++ )
Solve(k);
printf("%d\n", ans);
return 0;
}
T3 地铁
很容易发现原图是平面图,一个比较套路的想法是转化为对偶图跑最小割。
发现对偶图是一棵树的形态,而依赖关系可以看做对于树上的两条链,如果割掉一条链中的边,那么另一条链中也需要割掉一条边。
一个比较显然的想法是在两条链的链底连接一条双向的 \(inf\) 的边,具体如下图:
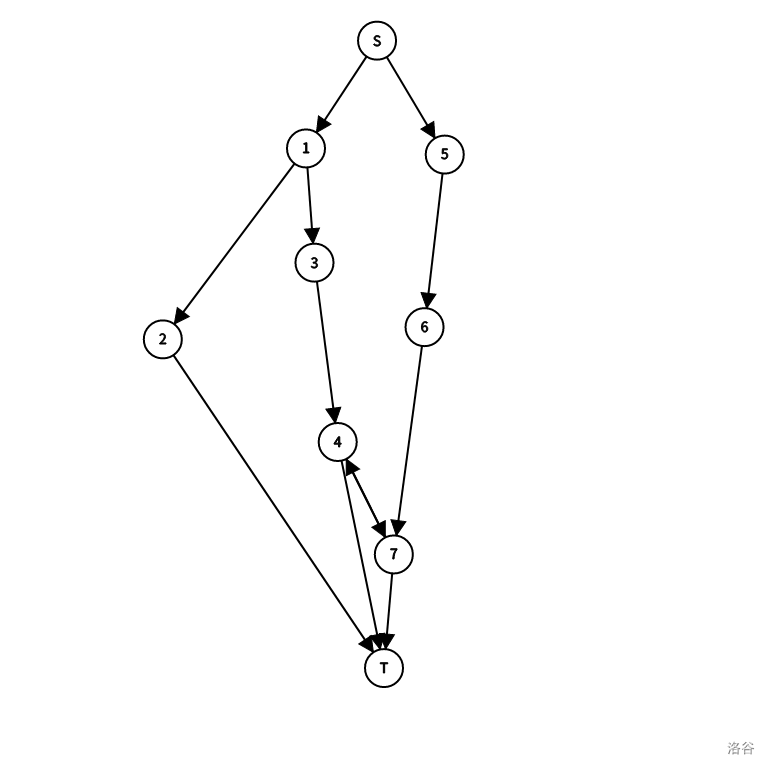
我们在 \(4,7\) 之间连接了权值为 \(inf\) 的边,限制是 \(S\to 4\) 与 \(S\to 7\) 这两条链,然而我们可以割掉 \(S\to 1\) 和 \(7\to T\) 这两条边,实际上 \(inf\) 边没有产生限制。
简单改进建模,对于两条有限制的链,从一条链的链底向另一条链中的每个点均建立流量为 \(inf\) 的边。
然而这样边数为 \(O(n^2)\) ,考虑到每次连接的均为一条链,因此建立一个与原树形态相同,边方向相反并且流量均为 \(inf\) 的图,此时只需要连接 \(O(n)\) 条边即可。
真正处理的过程需要进行一些改动,由于真正的限制一个点经过,另一个点必须经过并不好做,因此我们对限制取反,一个点不经过,另一个点一定不经过,考虑对于两个点分别找到完全包含它们的区间(不含边界)所对应的点 \(u,v\) ,在这两个点之间建立流量为 \(inf\) 的边,考虑此时的最小割,如果割掉 \(u\) 以上的边,那么 \(u\) 以下的边一定不会被割, \(v\) 以上的边就一定会被割,对应同时不经过的情况,如果割掉 \(u\) 以下的边,显然一定会割掉一条经过有依赖关系的点的边,发现此时只能割掉 \(v\) 以下的边,对应同时经过的情况。
code
#include <cstdio>
#include <algorithm>
#include <map>
using namespace std;
const int max1 = 1005;
const int inf = 0x3f3f3f3f;
int n, m, k, val[max1 + 5][max1 + 5], point[max1 + 5];
struct Line
{
int L, R, w;
Line () {}
Line ( int __L, int __R, int __w )
{ L = __L, R = __R, w = __w; }
bool operator < ( const Line &A ) const
{ return R - L < A.R - A.L; }
}A[max1 * 2 + 5];
map <int, int> tmp;
struct Graph_Net
{
int sum_point, Map[max1 * 2 + 5][2], s, t;
struct Node
{ int next, v, flow; } edge[max1 * 16 + 5];
int head[max1 * 4 + 5], now[max1 * 4 + 5], sum_edge;
int que[max1 * 4 + 5], L, R, dis[max1 * 4 + 5];
void Add ( int u, int v, int flow )
{
edge[++sum_edge].v = v;
edge[sum_edge].flow = flow;
edge[sum_edge].next = head[u];
head[u] = sum_edge;
return;
}
void Add_Edge ( int u, int v, int flow )
{ return Add(u, v, flow), Add(v, u, 0); }
void Clear ()
{ sum_point = sum_edge = 0; return; }
int Create ()
{ head[++sum_point] = 0; return sum_point; }
bool Bfs ()
{
for ( int i = 1; i <= sum_point; i ++ )
dis[i] = inf;
L = R = 1;
que[R] = s;
dis[s] = 0;
while ( L <= R )
{
int x = que[L++];
now[x] = head[x];
if ( x == t )
return true;
for ( int i = head[x]; i; i = edge[i].next )
{
int v = edge[i].v, flow = edge[i].flow;
if ( flow && dis[v] == inf )
{
dis[v] = dis[x] + 1;
que[++R] = v;
}
}
}
return false;
}
int Dfs ( int x, int sum )
{
if ( x == t )
return sum;
int res, k;
res = 0;
for ( int i = now[x]; i && sum; i = edge[i].next )
{
now[x] = i;
int v = edge[i].v, flow = edge[i].flow;
if ( flow && dis[v] == dis[x] + 1 )
{
k = Dfs(v, min(sum, flow));
if ( !k )
dis[v] = inf;
else
{
edge[i].flow -= k;
if ( i & 1 )
edge[i + 1].flow += k;
else
edge[i - 1].flow += k;
res += k;
sum -= k;
}
}
}
return res;
}
int Dinic ()
{
int ans = 0;
while ( Bfs() )
ans += Dfs(s, inf);
if ( ans >= inf )
ans = -1;
return ans;
}
}Graph;
int main ()
{
freopen("underground.in", "r", stdin);
freopen("underground.out", "w", stdout);
scanf("%d%d%d", &n, &m, &k);
for ( int i = 1; i <= n - 1; i ++ )
for ( int j = i + 1; j <= n; j ++ )
val[i][j] = inf;
int L, R, w;
for ( int i = 1; i <= m; i ++ )
{
scanf("%d%d%d", &L, &R, &w);
val[L][R] = min(val[L][R], w);
}
m = 0;
for ( int i = 1; i <= n - 1; i ++ )
{
for ( int j = i + 1; j <= n; j ++ )
{
if ( i + 1 == j )
A[++m] = Line(i, j, val[i][j]);
else if ( val[i][j] != inf )
A[++m] = Line(i, j, val[i][j]);
}
}
sort(A + 1, A + 1 + m);
tmp.clear();
Graph.Clear();
Graph.s = Graph.Create();
Graph.t = Graph.Create();
for ( int i = 1; i <= m; i ++ )
{
Graph.Map[i][0] = Graph.Create();
Graph.Map[i][1] = Graph.Create();
Graph.Add_Edge(Graph.Map[i][1], Graph.Map[i][0], inf);
if ( A[i].L + 1 != A[i].R )
{
while ( true )
{
auto it = tmp.lower_bound(A[i].L);
if ( it == tmp.end() || it -> first == A[i].R )
break;
Graph.Add_Edge(Graph.Map[i][0], Graph.Map[it -> second][0], A[it -> second].w);
Graph.Add_Edge(Graph.Map[it -> second][1], Graph.Map[i][1], inf);
tmp.erase(it);
}
}
else
Graph.Add_Edge(Graph.Map[i][0], Graph.t, inf);
tmp.insert(make_pair(A[i].L, i));
for ( int k = A[i].L + 1; k <= A[i].R - 1; k ++ )
if ( !point[k] )
point[k] = i;
}
for ( auto it : tmp )
Graph.Add_Edge(Graph.s, Graph.Map[it.second][0], A[it.second].w), Graph.Add_Edge(Graph.Map[it.second][1], Graph.s, inf);
for ( int i = 1, u, v; i <= k; i ++ )
{
scanf("%d%d", &u, &v);
u = point[u], v = point[v];
int u0, u1, v0, v1;
if ( u )
u0 = Graph.Map[u][0], u1 = Graph.Map[u][1];
else
u0 = u1 = Graph.s;
if ( v )
v0 = Graph.Map[v][0], v1 = Graph.Map[v][1];
else
v0 = v1 = Graph.s;
Graph.Add_Edge(u0, v1, inf);
Graph.Add_Edge(v0, u1, inf);
}
printf("%d\n", Graph.Dinic());
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号