2023省选武汉联测4
T1 挑战NPC
我们不对每个 \(d\) 分别求解答案,而是考虑枚举一个点集 \(S\) ,用 \(S\) 中距离最远的点的距离 \(dis\) 来更新 \(ans_{dis}\) 之后对 \(ans\) 数组进行一次前缀 \(\max\) 即可。容易发现本质不同的 \(S\) 中距离最远点的距离只有 \(n^2\) 中,因此考虑枚举两个点 \(a,b\) ,假设 \(dis(a,b)\) 为 \(S\) 集合中距离最远的点,枚举所有点并将 \(dis(i,a)\le dis(a,b)\ and\ dis(i,b)\le dis(a,b)\) 的点加入到 \(S\) 中,考虑对 \(S\) 集合中的点求解最大团,一个经典的结论是原图最大团为其补图的最大独立集,因此我们建立原图的补图,求解补图的最大独立集,具体的 \((i,j)\) 之间存在连边当且仅当 \(dis(i,j)>dis(a,b)\) ,发现此时形成的图是二分图,有经典结论:二分图最大独立集等于总点数减最大匹配数。直接建图跑网络流即可。
简单证明一下补图为什么是二分图,考虑两个点 \(A,B\) ,如下图:
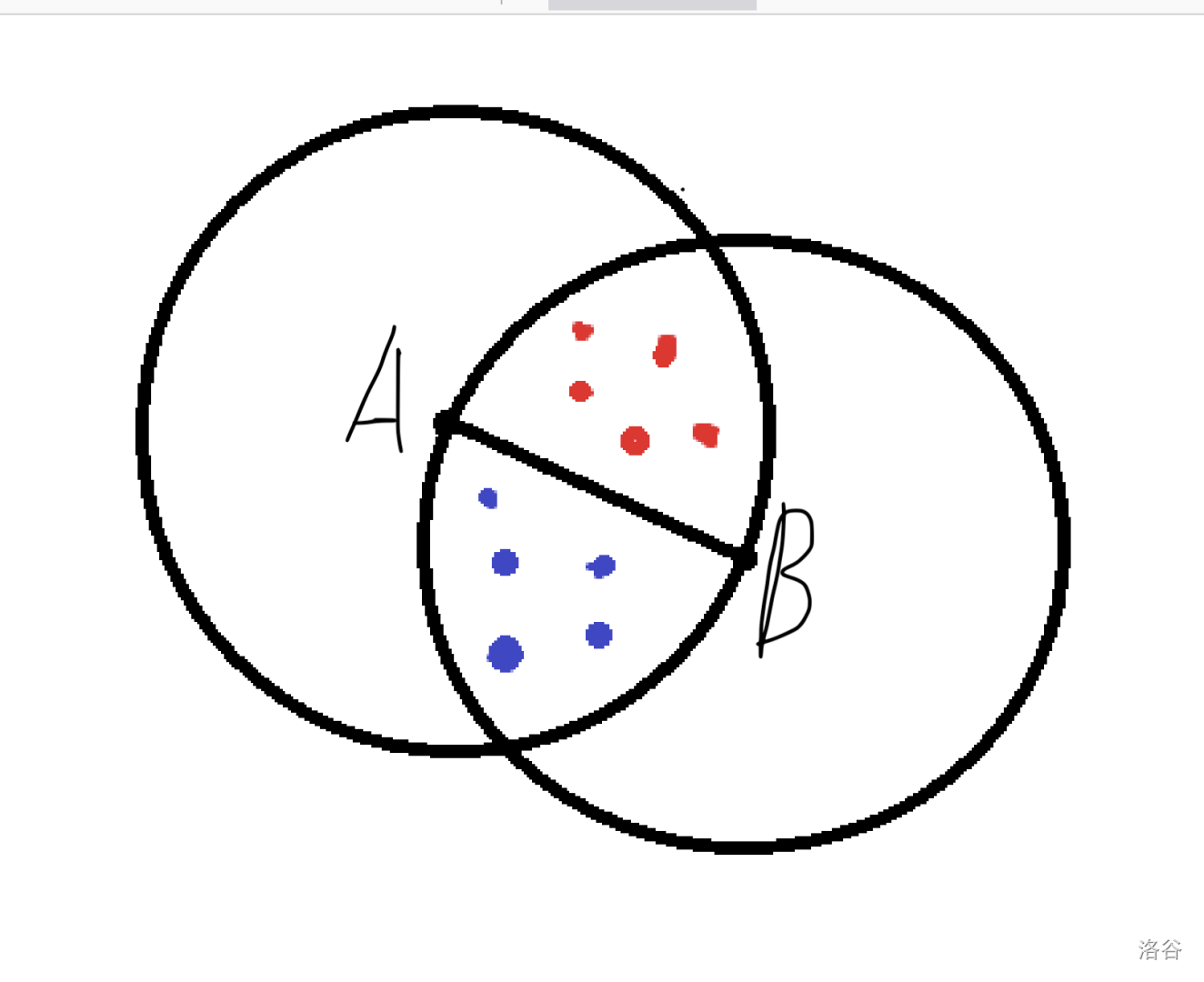
容易发现 \(S\) 集合中的点一定位于这两个圆的交集中,颜色相同的点之间不存在连边,颜色不同的点之间可能存在连边,得证。
code
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
const int max1 = 100, max2 = 1e5;
const int inf = 0x3f3f3f3f;
int n, m, x[max1 + 5], y[max1 + 5], dis[max1 + 5][max1 + 5];
int tmp[max1 + 5], len;
int ans[max2 + 5];
struct Node
{ int next, v, flow; } edge[max1 * max1 + 5];
int head[max1 + 5], now[max1 + 5], total;
vector <int> tmp_edge[max1 + 5];
int color[max1 + 5];
int s, t, deep[max1 + 5], que[max1 + 5], l, r;
void Add ( int u, int v, int flow )
{
edge[++total].v = v;
edge[total].flow = flow;
edge[total].next = head[u];
head[u] = total;
return;
}
void Add_Edge ( int u, int v, int flow )
{
Add(u, v, flow);
Add(v, u, 0);
return;
}
int Ceil_Sqrt ( long long x )
{
int l = 0, r = 1e6, res = 0;
while ( l <= r )
{
int mid = l + r >> 1;
if ( 1LL * mid * mid >= x )
res = mid, r = mid - 1;
else
l = mid + 1;
}
return res;
}
void Get_Color ( int now )
{
for ( auto v : tmp_edge[now] )
{
if ( !color[v] )
{
color[v] = 3 - color[now];
Get_Color(v);
}
}
return;
}
bool Bfs ()
{
for ( int i = 1; i <= t; i ++ )
deep[i] = inf;
deep[s] = 0;
l = 1, r = 0;
que[++r] = s;
while ( l <= r )
{
int x = que[l++];
now[x] = head[x];
if ( x == t )
return true;
for ( int i = head[x]; i; i = edge[i].next )
{
int v = edge[i].v, flow = edge[i].flow;
if ( flow > 0 && deep[v] == inf )
{
deep[v] = deep[x] + 1;
que[++r] = v;
}
}
}
return false;
}
int Dfs ( int x, int sum )
{
if ( x == t )
return sum;
int res = 0;
for ( int i = now[x]; i && sum; i = edge[i].next )
{
int v = edge[i].v, flow = edge[i].flow;
if ( flow > 0 && deep[v] == deep[x] + 1 )
{
int k = Dfs(v, min(sum, flow));
if ( !k )
deep[v] = inf;
else
{
edge[i].flow -= k;
if ( i & 1 )
edge[i + 1].flow += k;
else
edge[i - 1].flow += k;
sum -= k;
res += k;
}
}
}
return res;
}
void Solve ( int A, int B )
{
int max_dis = dis[A][B];
if ( max_dis > m )
return;
len = 0;
tmp[++len] = A;
tmp[++len] = B;
for ( int i = 1; i <= n; i ++ )
if ( i != A && i != B && dis[i][A] <= max_dis && dis[i][B] <= max_dis )
tmp[++len] = i;
total = 0;
for ( int i = 1; i <= len + 2; i ++ )
head[i] = 0, tmp_edge[i].clear(), color[i] = 0;
for ( int i = 1; i <= len; i ++ )
for ( int j = 1; j <= len; j ++ )
if ( i != j && dis[tmp[i]][tmp[j]] > max_dis )
tmp_edge[i].push_back(j);
for ( int i = 1; i <= len; i ++ )
{
if ( !color[i] )
{
color[i] = 1;
Get_Color(i);
}
}
for ( int i = 1; i <= len; i ++ )
for ( int j = 1; j <= len; j ++ )
if ( color[i] < color[j] && dis[tmp[i]][tmp[j]] > max_dis )
Add_Edge(i, j, 1);
s = len + 1, t = len + 2;
for ( int i = 1; i <= len; i ++ )
{
if ( color[i] == 1 )
Add_Edge(s, i, 1);
else
Add_Edge(i, t, 1);
}
int res = 0;
while ( Bfs() )
res += Dfs(s, inf);
res = len - res;
ans[max_dis] = max(ans[max_dis], res);
return;
}
int main ()
{
freopen("challenge.in", "r", stdin);
freopen("challenge.out", "w", stdout);
scanf("%d%d", &n, &m);
for ( int i = 1; i <= n; i ++ )
scanf("%d%d", &x[i], &y[i]);
for ( int i = 1; i <= n; i ++ )
for ( int j = 1; j <= n; j ++ )
dis[i][j] = Ceil_Sqrt(1LL * ( x[i] - x[j] ) * ( x[i] - x[j] ) + 1LL * ( y[i] - y[j] ) * ( y[i] - y[j] ));
ans[0] = 1;
for ( int i = 1; i <= n; i ++ )
for ( int j = i + 1; j <= n; j ++ )
Solve(i, j);
for ( int i = 1; i <= m; i ++ )
ans[i] = max(ans[i], ans[i - 1]);
for ( int i = 0; i <= m; i ++ )
printf("%d ", ans[i]);
printf("\n");
return 0;
}
T2 糖果大赛
发现先手获胜的局面很多,因此考虑求解先手失败的局面。
容易发现一种数字我们不关心其出现的次数,因此我们用一个不可重集合维护当前序列中出现了哪些数,比较显然的是 \(\{1\}\) 和 \(\{2\}\) 一定是先手失败, \(\{1,2\}\) 是先手获胜,考虑推测 \(\max(S)\ge 3\) 的情况,假设 \(S\) 中存在奇数,先手可以令 \(w=2\) 进行操作,容易发现先手必胜,于是考虑 \(S\) 中只存在偶数的情况,假设 \(S\) 中存在 \(\operatorname{mod} 4=2\) 的数,先手可以令 \(w=4\) 进行操作,容易发现此时先手必胜,因此考虑 \(S\) 中只存在 \(4\) 的倍数的情况,比较不幸的是,当 \(S\) 中存在 \(\operatorname{mod} 8=4\) 的数时,我们不能令 \(w=8\) 来构造,后手显然可以令 \(w=3\) 来获得必胜局面,但是容易发现当 \(S\) 中存在 \(\operatorname{mod} 3=1\) 或 \(\operatorname{mod} 3=2\) 的数中的一种,先手必胜,因此先手失败的必要条件为同时存在 \(\operatorname{mod} 3=1\) 和 \(\operatorname{mod} 3=2\) 的数或者 \(S\) 中均为 \(3\) 的倍数。
将两种条件简单结合,先手必败的第一种情况为 \(S\) 中存在 \(4\) 的倍数并且同时存在 \(\operatorname{mod} 3=1\) 和 \(\operatorname{mod} 3=2\) 的数,打表发现必败局面只存在 \({4,8}\) ,当集合中元素更大时,先手可以令 \(w=12\) 得到必胜局面。
第二种情况为 \(S\) 中元素均为 \(12\) 的倍数,由于 \(a_i\le 200\) ,此时只存在 \(16\) 种不同的数,暴力求解必败状态用状压求解方案数即可。
code
#include <cstdio>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
const int max1 = 200, max2 = 16, max3 = 1 << 16;
const int mod = 998244353;
int n, a[max1 + 5], sum;
int b[max2 + 5];
bool f[max3 + 5];
map < vector <int>, bool > Map;
int g[max1 + 5][max3 + 5];
void Add ( int &x, int y )
{
x = x + y;
if ( x >= mod )
x = x - mod;
return;
}
bool Dfs ( const vector <int> &now )
{
if ( now.empty() )
return true;
else if ( Map.find(now) != Map.end() )
return Map[now];
vector <int> tmp;
int Max = 0;
for ( auto val : now )
Max = max(Max, val);
for ( int i = 1; i <= Max; i ++ )
{
tmp.clear();
for ( auto v : now )
if ( v % i )
tmp.push_back(v % i);
sort(tmp.begin(), tmp.end());
tmp.resize(unique(tmp.begin(), tmp.end()) - tmp.begin());
if ( !Dfs(tmp) )
{
Map[now] = true;
return true;
}
}
Map[now] = false;
return false;
}
int main ()
{
freopen("candy.in", "r", stdin);
freopen("candy.out", "w", stdout);
scanf("%d", &n);
sum = 1;
for ( int i = 1; i <= n; i ++ )
scanf("%d", &a[i]), sum = 1LL * sum * a[i] % mod;
int delta = 1;
for ( int i = 1; i <= n; i ++ )
delta = 1LL * delta * ( a[i] >= 1 ) % mod;
sum = ( sum - delta + mod ) % mod;
delta = 1;
for ( int i = 1; i <= n; i ++ )
delta = 1LL * delta * ( a[i] >= 2 ) % mod;
sum = ( sum - delta + mod ) % mod;
delta = 1;
for ( int i = 1; i <= n; i ++ )
delta = 1LL * delta * ( ( a[i] >= 8 ) + ( a[i] >= 4 ) ) % mod;
sum = ( sum - delta + mod ) % mod;
delta = 1;
for ( int i = 1; i <= n; i ++ )
delta = 1LL * delta * ( a[i] >= 4 ) % mod;
sum = ( sum + delta ) % mod;
for ( int i = 1; i <= n; i ++ )
delta = 1LL * delta * ( a[i] >= 8 ) % mod;
sum = ( sum + delta ) % mod;
for ( int i = 1; i <= max2; i ++ )
b[i] = i * 12;
vector <int> tmp;
for ( int s = 0; s < max3; s ++ )
{
tmp.clear();
for ( int i = 1; i <= max2; i ++ )
if ( s >> i - 1 & 1 )
tmp.push_back(b[i]);
f[s] = Dfs(tmp);
}
g[0][0] = 1;
for ( int i = 1; i <= n; i ++ )
for ( int s = 0; s < max3; s ++ )
for ( int k = 1; k <= max2; k ++ )
if ( b[k] <= a[i] )
Add(g[i][s | 1 << k - 1], g[i - 1][s]);
for ( int s = 0; s < max3; s ++ )
if ( !f[s] )
Add(sum, mod - g[n][s]);
printf("%d\n", sum);
return 0;
}
T3 聚会
首先需要知道一些简单的结论???
结论一:
翻转的区间两两有交。
假设没有交集,简单画图发现此时一定不优。
结论二:
设翻转前第 \(i\) 个位置覆盖次数为 \(a_i\) ,翻转后第 \(i\) 个位置覆盖的次数为 \(b_i\) ,设翻转的区间的交集为 \([x,y]\) , \([x,y]\) 中 \(b_i\) 最大的位置记为 \(t\) ,可以观察发现:
\(b_t\ge \max(b)-1\) ,考虑反证,如果 \(b_t\le \max(b)-2\) ,此时找到一个 \(l=x\) 的区间和一个 \(r=y\) 的区间,容易发现不翻转这两个区间一定更优,反复进行这种操作,容易发现最终 \(b_t\ge \max(b)-1\) 。
\(a_t\ge \max(a)\) ,仍然考虑反证,容易发现 \(\max(a)\) 不可能在 \([x,y]\) 区间内被取到,否则 \(b_t\) 一定不是区间内最大值,因此至少存在一个区间没有覆盖到 \(\max(a)\) ,设 \(\max(a)\) 被取到的位置为 \(k\) ,那么有 \(a_t-b_t-1\ge a_k-b_k\) ,简单移项发现 \(b_k-b_t\ge 2\) 与上一条矛盾。
考虑如何处理原问题,首先一个初步的想法是二分 \(\max(b)\) 为 \(lim\) ,由于 \(b_t\ge \max(b)-1\) ,因此我们讨论 \(b_t=\max(b)-1\) 或 \(b_t=\max(b)\) ,设翻转的区间个数为 \(sum\) ,容易发现 \(b_t-a_t=sum\) ,因此我们可以直接求出 \(sum\) 的数值,考虑进行 Check ,由于 \(\max(a)\) 所在的位置一定位于 \([x,y]\) 内,因此我们考虑将区间按照 \(l\) 进行排序,依次扫左端点位于 \([1,t]\) 内所有的区间,假设当前扫到了第 \(i\) 个位置,设之前翻转的所有区间个数为 \(cnt\) ,容易发现我们还需要翻转 \(max(0,\lceil\tfrac{a_i+sum-lim}{2}\rceil-cnt)\) 个区间,为了尽量减少对右区间的影响,我们贪心的选择右端点最靠右的翻转即可。
code
#include <cstdio>
#include <vector>
#include <utility>
#include <algorithm>
#include <queue>
using namespace std;
const int max1 = 2e5;
int n, m;
long long A[max1 + 5], B[max1 + 5];
vector < pair <int, int> > bin[max1 + 5];
priority_queue < pair <int, int>, vector < pair <int, int> >, less < pair <int, int> > > que;
bool Check ( int pos, long long lim, long long sum )
{
while ( !que.empty() )
que.pop();
for ( int i = 0; i <= n; i ++ )
B[i] = 0;
long long cnt = 0;
for ( int i = 1; i <= pos; i ++ )
{
for ( auto val : bin[i] )
if ( val.first > pos )
que.push(val);
long long k = ( A[i] + sum - lim + 1 ) / 2;
while ( cnt < k )
{
if ( que.empty() )
return false;
pair <int, int> now = que.top();
que.pop();
long long del = min(1LL * now.second, k - cnt);
cnt += del;
now.second -= del;
B[pos + 1] -= del;
B[now.first] += del << 1;
if ( now.second )
que.push(now);
}
}
for ( int i = pos + 1; i <= n; i ++ )
{
B[i] += B[i - 1];
if ( A[i] + B[i] > lim )
return false;
}
return true;
}
int main ()
{
freopen("party.in", "r", stdin);
freopen("party.out", "w", stdout);
scanf("%d%d", &n, &m);
for ( int i = 1, a, b, c; i <= m; i ++ )
{
scanf("%d%d%d", &a, &b, &c);
if ( a > b )
swap(a, b);
A[a] += c;
A[b] -= c;
bin[a].push_back(make_pair(b, c));
}
int pos = 0;
for ( int i = 1; i <= n; i ++ )
{
A[i] += A[i - 1];
if ( A[pos] < A[i] )
pos = i;
}
long long l = 1, r = A[pos], ans = A[pos];
while ( l <= r )
{
long long mid = l + r >> 1;
if ( Check(pos, mid, A[pos] - mid) || Check(pos, mid, A[pos] - mid + 1) )
ans = mid, r = mid - 1;
else
l = mid + 1;
}
printf("%lld\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号