2023省选武汉联测1
T1 递归函数
首先考虑进制 \(B\) 为质数的情况,由于答案是 \(f(n,m)\) 中因子 \(B\) 的个数,此时指数可以用加法直接合并,那么有比较暴力的思路是直接递推,复杂度为 \(O(nm)\) ,考虑求解一种类似通项公式的东西,容易发现 \(f(n,m)=\prod_{x=1}^{\infty}x^\binom{n-x+m-1}{m-1}\) ,因此我们的答案为 \(\sum_{i=1}^{\infty}\sum_{k=1}^{\infty}\binom{n-kB^i+m-1}{m-1}\) ,发现 \(i\) 的范围为 \(\log\) 级别,因此可以直接枚举,对于后面一部分,发现这大约是一个 \(m+1\) 次多项式,直接拉格朗日插值进行求解即可。
此时我们考虑 \(B\) 为合数的情况,当 \(B=6,10\) 时,根据通项公式容易猜想到因子 \(3,5\) 的个数一定比 \(2\) 多,因此直接令 \(B=3,5\) 进行求解即可,当 \(B=4,8,9\) 时,设当 \(B=2,3\) 的答案为 \(ans\) (不对 \(mod\) 取模),那么我们需要求解 \(\lfloor\tfrac{ans}{2}\rfloor\) 或者 \(\lfloor\tfrac{ans}{3}\rfloor\) ,由于 \(\lfloor\tfrac{ans}{2}\rfloor=\tfrac{ans-ans\operatorname{mod}2}{2}\) ,因此可以将 \(mod\) 改为 \(2,3\) 进行求解。
code
#include <cmath>
#include <cstdio>
using namespace std;
const int max1 = 16;
const int mod = 998444353;
int inv[max1 + 5], ifac[max1 + 5], y[max1 + 5];
int Quick_Power ( int base, int p, int P )
{
int res = 1;
while ( p )
{
if ( p & 1 )
res = 1LL * res * base % P;
p >>= 1;
base = 1LL * base * base % P;
}
return res;
}
int C ( int n, int m, int P )
{
if ( n < m || n < 0 || m < 0 )
return 0;
int ans = 1;
for ( int i = n; i >= n - m + 1; i -- )
ans = 1LL * ans * i % P;
ans = 1LL * ans * ifac[m] % P;
return ans;
}
int Lucas ( int n, int m, int P )
{
if ( n < m || n < 0 || m < 0 )
return 0;
int ans = 1;
while ( n && m )
{
ans = 1LL * ans * C(n % P, m % P, P) % P;
n /= P, m /= P;
}
return ans;
}
struct Data
{
int x, y, P;
Data () {}
Data ( int __x, int __y, int __P )
{ x = __x, y = __y, P = __P; }
void equil ( int val, int m )
{
P = m;
x = y = 0;
while ( !( val % P ) )
++y, val /= P;
x = ( val % P + P ) % P;
return;
}
Data operator * ( const Data &A ) const
{ return Data(1LL * x * A.x % P, y + A.y, P); }
Data operator / ( const Data &A ) const
{ return Data(1LL * x * Quick_Power(A.x, P - 2, P) % P, y - A.y, P); }
};
int Lagrange ( int c, int x, int P )
{
if ( x <= c )
return y[x];
int ans = 0;
for ( int i = 1; i <= c; i ++ )
{
Data prod, tmp;
prod.equil(1, P);
for ( int j = 1; j <= c; j ++ )
{
if ( i == j )
continue;
tmp.equil(x - j, P);
prod = prod * tmp;
tmp.equil(i - j, P);
prod = prod / tmp;
}
ans = ( ans + 1LL * ( prod.y ? 0 : prod.x ) * y[i] ) % P;
}
return ans;
}
int Work ( int n, int m, int B, int P )
{
inv[1] = 1;
for ( int i = 2; i <= max1 + 4; i ++ )
inv[i] = 1LL * ( P - P / i ) * inv[P % i] % P;
ifac[0] = inv[1];
for ( int i = 1; i <= max1 + 4; i ++ )
ifac[i] = 1LL * ifac[i - 1] * inv[i] % P;
y[0] = 0;
for ( int x = 1; x <= m + 3; x ++ )
{
y[x] = ( y[x - 1] + Lucas(n - x * B + m - 1, m - 1, P) ) % P;
}
return Lagrange(m + 3, n / B, P);
}
int Solve ( int n, int m, int B, int P )
{
int ans = 0;
int power = B;
while ( power <= n )
{
ans = ( ans + Work(n, m, power, P) ) % P;
power = power * B;
}
return ans;
}
int main ()
{
freopen("function.in", "r", stdin);
freopen("function.out", "w", stdout);
int n, m, B, ans;
scanf("%d%d%d", &n, &m, &B);
if ( B == 4 )
ans = 1LL * ( Solve(n, m, 2, mod) - Solve(n, m, 2, 2) + mod ) * Quick_Power(2, mod - 2, mod) % mod;
else if ( B == 6 )
ans = Solve(n, m, 3, mod);
else if ( B == 8 )
ans = 1LL * ( Solve(n, m, 2, mod) - Solve(n, m, 2, 3) + mod ) * Quick_Power(3, mod - 2, mod) % mod;
else if ( B == 9 )
ans = 1LL * ( Solve(n, m, 3, mod) - Solve(n, m, 3, 2) + mod ) * Quick_Power(2, mod - 2, mod) % mod;
else if ( B == 10 )
ans = Solve(n, m, 5, mod);
else
ans = Solve(n, m, B, mod);
printf("%d\n", ans);
return 0;
}
T2 火力规划
可以发现一个三角形能够被拆分为如下形式:
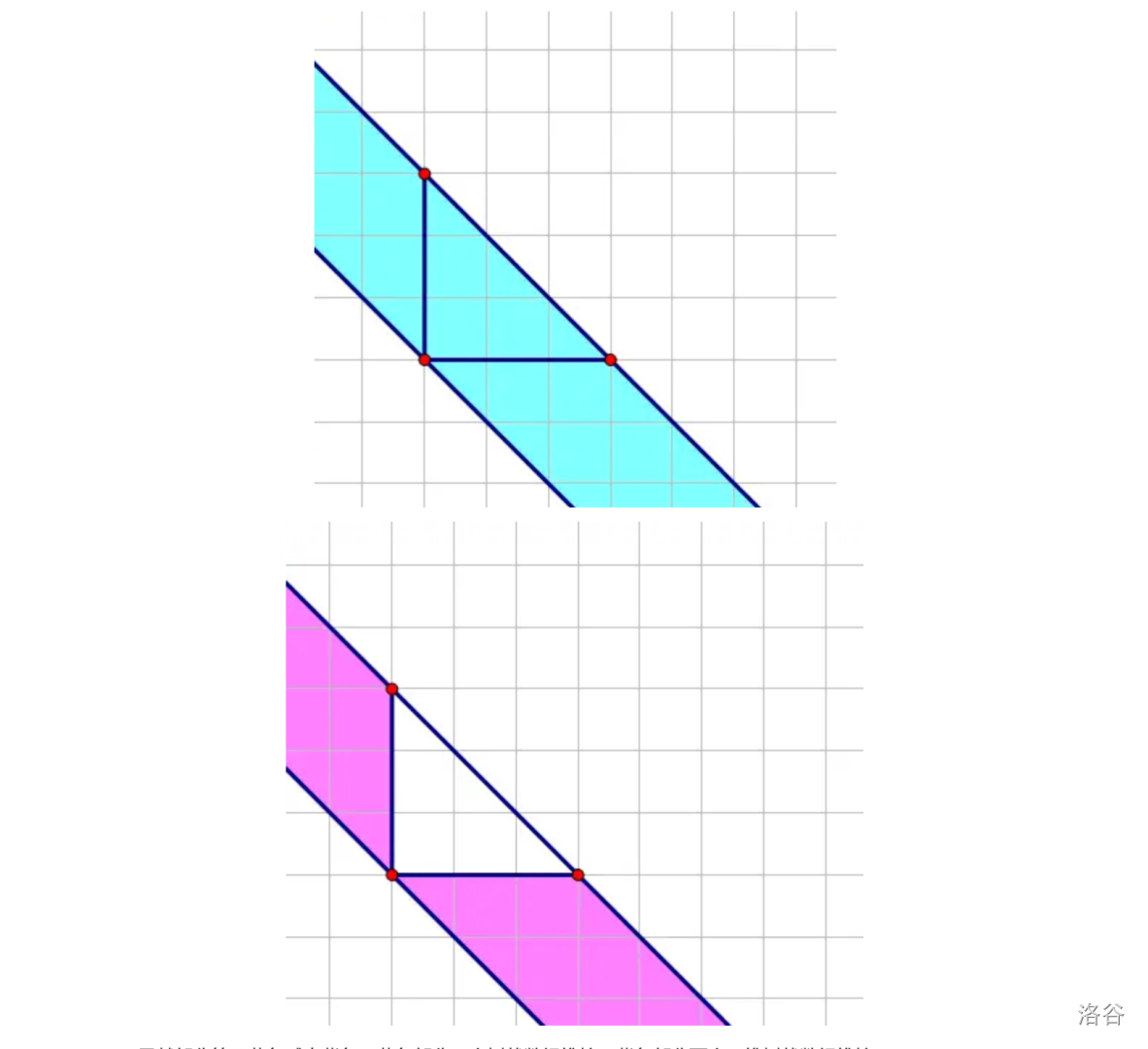
蓝色部分可以用一个树状数组维护,紫色部分用两个二维树状数组维护。
code
#include <cstdio>
#include <cstring>
using namespace std;
const int max1 = 5000, max2 = 1e5;
int n, q, ans[max2 + 5];
struct Question
{ int opt, dir, x, y, r; }qus[max2 + 5];
#define lowbit(now) ( now & -now )
struct Bit1
{
int tree[max1 * 3 + 5];
void Clear ()
{ memset(tree, 0, sizeof(tree)); return; }
void Insert ( int now, int val )
{
while ( now <= max1 + n + n )
{
tree[now] += val;
now += lowbit(now);
}
return;
}
void Insert ( int l, int r, int val )
{
Insert(l, val);
Insert(r + 1, -val);
return;
}
int Query ( int now )
{
int res = 0;
while ( now )
{
res += tree[now];
now -= lowbit(now);
}
return res;
}
}Tree1;
struct Bit2
{
int tree[max1 * 2 + 5][max1 + 5];
void Clear ()
{ memset(tree, 0, sizeof(tree)); return; }
void Insert ( int x, int y, int val )
{
for ( int i = x; i <= max1 + n; i += lowbit(i) )
for ( int j = y; j <= n; j += lowbit(j) )
tree[i][j] += val;
return;
}
void Insert ( int x1, int x2, int y1, int y2, int val )
{
Insert(x1, y1, val);
Insert(x1, y2 + 1, -val);
Insert(x2 + 1, y1, -val);
Insert(x2 + 1, y2 + 1, val);
return;
}
int Query ( int x, int y )
{
int res = 0;
for ( int i = x; i; i -= lowbit(i) )
for ( int j = y; j; j -= lowbit(j) )
res += tree[i][j];
return res;
}
}Tree2, Tree3;
int main ()
{
freopen("planning.in", "r", stdin);
freopen("planning.out", "w", stdout);
scanf("%d%d", &n, &q);
for ( int i = 1; i <= q; i ++ )
{
scanf("%d", &qus[i].opt);
if ( qus[i].opt == 1 )
scanf("%d%d%d%d", &qus[i].dir, &qus[i].x, &qus[i].y, &qus[i].r);
else
scanf("%d%d", &qus[i].x, &qus[i].y);
}
Tree1.Clear();
Tree2.Clear();
Tree3.Clear();
for ( int i = 1; i <= q; i ++ )
{
if ( qus[i].opt == 1 )
{
if ( qus[i].dir == 1 )
{
int x = qus[i].x, y = qus[i].y, r = qus[i].r;
Tree1.Insert(x + y, x + y + r, 1);
Tree2.Insert(x + y, x + y + r, 1, x - 1, -1);
Tree3.Insert(x + y, x + y + r, 1, y - 1, -1);
}
}
else
{
int x = qus[i].x, y = qus[i].y;
ans[i] += Tree1.Query(x + y) + Tree2.Query(x + y, x) + Tree3.Query(x + y, y);
}
}
Tree1.Clear();
Tree2.Clear();
Tree3.Clear();
for ( int i = 1; i <= q; i ++ )
{
if ( qus[i].opt == 1 )
{
if ( qus[i].dir == 2 )
{
int x = qus[i].x, y = qus[i].y, r = qus[i].r;
Tree1.Insert(x - y + max1, x - y + r + max1, 1);
Tree2.Insert(x - y + max1, x - y + r + max1, 1, x - 1, -1);
Tree3.Insert(x - y + max1, x - y + r + max1, y + 1, n, -1);
}
}
else
{
int x = qus[i].x, y = qus[i].y;
ans[i] += Tree1.Query(x - y + max1) + Tree2.Query(x - y + max1, x) + Tree3.Query(x - y + max1, y);
}
}
Tree1.Clear();
Tree2.Clear();
Tree3.Clear();
for ( int i = 1; i <= q; i ++ )
{
if ( qus[i].opt == 1 )
{
if ( qus[i].dir == 3 )
{
int x = qus[i].x, y = qus[i].y, r = qus[i].r;
Tree1.Insert(x - y - r + max1, x - y + max1, 1);
Tree2.Insert(x - y - r + max1, x - y + max1, x + 1, n, -1);
Tree3.Insert(x - y - r + max1, x - y + max1, 1, y - 1, -1);
}
}
else
{
int x = qus[i].x, y = qus[i].y;
ans[i] += Tree1.Query(x - y + max1) + Tree2.Query(x - y + max1, x) + Tree3.Query(x - y + max1, y);
}
}
Tree1.Clear();
Tree2.Clear();
Tree3.Clear();
for ( int i = 1; i <= q; i ++ )
{
if ( qus[i].opt == 1 )
{
if ( qus[i].dir == 4 )
{
int x = qus[i].x, y = qus[i].y, r = qus[i].r;
Tree1.Insert(x + y - r, x + y, 1);
Tree2.Insert(x + y - r, x + y, x + 1, n, -1);
Tree3.Insert(x + y - r, x + y, y + 1, n, -1);
}
}
else
{
int x = qus[i].x, y = qus[i].y;
ans[i] += Tree1.Query(x + y) + Tree2.Query(x + y, x) + Tree3.Query(x + y, y);
}
}
for ( int i = 1; i <= q; i ++ )
if ( qus[i].opt == 2 )
printf("%d\n", ans[i]);
return 0;
}
T3 再生核希尔伯特空间
考虑一种比较套路的做法:根号分治,对于大于长度 \(\sqrt{m}\) 的串,发现这种串不会超过 \(\sqrt{m}\) 个,因此可以预处理 \(f_{i,j}\) 表示串 \(i\) 在串 \(j\) 中出现了几次,其中 \(len_j>\sqrt{m}\) ,查询时可以直接前缀和相减,预处理的过程可以首先对所有串建立 AC 自动机,查询时每当经过 AC 上一个节点,令当前节点权值 \(+1\) ,然后对整个 AC 自动机 Dfs 即可。
对于长度小于等于 \(\sqrt{m}\) 的串,由于这个串遍历 AC 自动机时经过的节点不会超过 \(\sqrt{m}\) 个,因此可以在 AC 自动机每个节点维护主席树,这样可以做到 \(O(\log n)\) 查询 \([l,r]\) 区间对每个节点的贡献,总复杂度为 \(O(m\sqrt{m}\log n)\) 。(离线后可以使用树状数组)
code
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
const int max1 = 162754;
const int B = 403;
int n, len[max1 + 5], pos[max1 + 5];
int sum[B + 5][max1 + 5], Map[max1 + 5], cnt;
long long ans[max1 + 5];
string str[max1 + 5];
struct Question
{
int l, r, id;
Question () {}
Question ( int __l, int __r, int __id )
{ l = __l, r = __r, id = __id; }
};
struct Bit
{
#define lowbit(now) ( now & -now )
int tree[max1 + 5];
void Clear ()
{ memset(tree, 0, sizeof(tree)); return; }
void Insert ( int now, int x )
{
while ( now <= n )
{
tree[now] += x;
now += lowbit(now);
}
return;
}
int Query ( int now )
{
int res = 0;
while ( now )
{
res += tree[now];
now -= lowbit(now);
}
return res;
}
int Query ( int l, int r )
{ return Query(r) - Query(l - 1); }
}Tree;
struct Aho_Corasick_Automaton
{
int son[max1 + 5][26], father[max1 + 5], fail[max1 + 5], val[max1 + 5], total;
vector <int> id[max1 + 5], edge[max1 + 5];
vector <Question> qus[max1 + 5];
queue <int> que;
void Clear ()
{
total = 0;
memset(son[0], 0, sizeof(son[0]));
father[0] = -1;
id[0].clear();
qus[0].clear();
return;
}
int Insert ( const string &s, const int &len, const int &val )
{
int now = 0;
for ( int i = 0; i < len; i ++ )
{
if ( !son[now][s[i] - 'a'] )
{
son[now][s[i] - 'a'] = ++total;
memset(son[total], 0, sizeof(son[total]));
father[total] = now;
id[total].clear();
qus[total].clear();
}
now = son[now][s[i] - 'a'];
}
id[now].push_back(val);
return now;
}
void Build ()
{
while ( !que.empty() )
que.pop();
fail[0] = -1;
for ( int i = 0; i < 26; i ++ )
{
if ( son[0][i] )
{
fail[son[0][i]] = 0;
que.push(son[0][i]);
}
}
while ( !que.empty() )
{
int now = que.front();
que.pop();
for ( int i = 0; i < 26; i ++ )
{
if ( !son[now][i] )
son[now][i] = son[fail[now]][i];
else
fail[son[now][i]] = son[fail[now]][i], que.push(son[now][i]);
}
}
for ( int i = 1; i <= total; i ++ )
edge[fail[i]].push_back(i);
return;
}
void Query ( int now, int *res )
{
for ( int v : edge[now] )
Query(v, res), val[now] += val[v];
for ( int v : id[now] )
res[v] = val[now];
return;
}
void Query ( const string &s, const int &len, int *res )
{
int now = 0;
for ( int i = 1; i <= total; i ++ )
val[i] = 0;
for ( int i = 0; i < len; i ++ )
{
now = son[now][s[i] - 'a'];
++val[now];
}
Query(0, res);
return;
}
void Dfs ( int now )
{
for ( int v : id[now] )
Tree.Insert(v, 1);
for ( Question v : qus[now] )
ans[v.id] += Tree.Query(v.l, v.r);
for ( int v : edge[now] )
Dfs(v);
for ( int v : id[now] )
Tree.Insert(v, -1);
return;
}
}AC;
int main ()
{
freopen("rkhs.in", "r", stdin);
freopen("rkhs.out", "w", stdout);
int q, l, r, k;
scanf("%d%d", &n, &q);
AC.Clear();
for ( int i = 1; i <= n; i ++ )
{
cin >> str[i];
len[i] = str[i].size();
pos[i] = AC.Insert(str[i], len[i], i);
}
AC.Build();
for ( int i = 1; i <= n; i ++ )
{
if ( len[i] > B )
{
Map[i] = ++cnt;
AC.Query(str[i], len[i], sum[cnt]);
for ( int j = 1; j <= n; j ++ )
sum[cnt][j] += sum[cnt][j - 1];
}
}
for ( int i = 1; i <= q; i ++ )
{
scanf("%d%d%d", &l, &r, &k);
if ( len[k] <= B )
{
int now = pos[k];
while ( now )
{
AC.qus[now].push_back(Question(l, r, i));
now = AC.father[now];
}
}
else
ans[i] = sum[Map[k]][r] - sum[Map[k]][l - 1];
}
Tree.Clear();
AC.Dfs(0);
for ( int i = 1; i <= q; i ++ )
printf("%lld\n", ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号