2021 ICPC EC Final B. Beautiful String 题解

2021 ICPC EC Final B. Beautiful String 题解

题意

问给定字符串t的所有子串中形如"114514"分割方案之和。其中'1'、'4'、'5'表示某一字符串，且可重复。

分析（暴力\(n^3\)）

记lcp[i][j]表示后缀i和j的最长公共前缀，那么如果lcp[i][j] >= j - i则说明i 到j这一段字符串在j之后重复出现了。可以使用\(n^2\)的dp预处理：lcp[i][j]= s[i]==s[j] ? lcp[i + 1][j + 1] + 1 : 0。

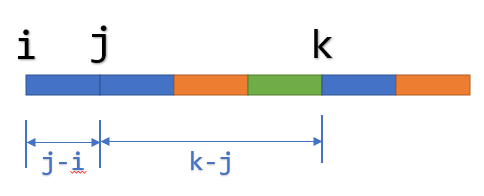
在\(n^2\)枚举i和j判断出lcp[i][j] >= j - i之后，枚举k，若lcp[j][k]比j - i大，则答案需要加上这一部分lcp[j][k]减掉j - i的长度，当然为了保证绿色部分至少存在1个，k要从j + 3开始枚举，而且要保证lcp[j][k]不能超出了k - j - 1。

代码（TLE）

#include <bits/stdc++.h>
using namespace std;

const int N = 5005;

char s[N];

int main() {
    int tt;
    scanf("%d",&tt);
    while(tt--) {
        scanf("%s",s+1);
        int n = strlen(s + 1);
        vector<vector<int>> lcp(n + 2, vector<int>(n + 2));
        for (int i = n; i >= 1; i--)
            for (int j = n; j >= i; j--)
                if (s[i] == s[j]) lcp[i][j] = lcp[i + 1][j + 1] + 1;
        long long ans = 0;
        for (int i = 1; i <= n; i++)
            for (int j = i + 1; j <= n; j++)
                if (lcp[i][j] >= j - i) {
                    for (int k = j + 3; k <= n; k++) {
                        if (lcp[j][k] > j - i) {
                            int mi = min(lcp[j][k], k - j - 1) - (j - i);
                            ans += max(mi, 0);
                        }
                    }
                }
        printf("%lld\n",ans);
    }
}

分析（预处理\(n^2\)）

对于上述过程，i、j、k是同时枚举的，std的优化是先枚举i、j，将j对后缀的贡献记录下来，再枚举j、k。

对于一个合法的i、j即lcp[i][j] >= j - i，若存在k对答案有贡献，那么lcp[j][k]也至少要是j - i，换句话说，从j往后j - i到整个字符串末尾都有可能会产生贡献。

记sum[j][len]表示从j开始长度为len的贡献，那么若lcp[i][j] >= j - i，sum[j][j - i]、sum[j][j - i + 1]、...、sum[j][length(s) - 1]、sum[j][length(s)]都要+1，当之后枚举j、k的时候如果满足条件了，我们应该从j - i开始加到长度min(lcp[j][k], k - j - 1) - 1这一段的sum值，也就是sum[j][j - i] + sum[j][j - i + 1] + ... + sum[j][min(lcp[j][k], k - j - 1) - 2]、sum[j][min(lcp[j][k], k - j - 1) - 1]。

对上述一些操作进行优化：

"sum[j][j - i]、sum[j][j - i + 1]、...、sum[j][length(s) - 1]、sum[j][length(s)]都要+1"

其实是对一段后缀同时加，可以使用差分优化，即sum[j][j - i] + 1、sum[j][length(s) + 1] - 1，只不过后续根本用不到sum[j][length(s) + 1]，所以只需要对sum[j][j - i] + 1，然后求前缀和即可。

"枚举j、k的时候，我们应该从j开始加上长度min(lcp[j][k], k - j - 1) - 1这一段的sum值"

其实是求一段前缀和，而求前缀和的原始数组就是上面差分数组计算出来的数组。

所以只要在枚举i、j的时候只统计差分数组的贡献，然后求两遍前缀和，就得到了sum数组的前缀和，这里不妨直接将sum先作为差分数组使用，在其的基础上做两遍前缀和将其转化为前缀和数组即可。这样就能够在枚举j、k的时候\(O(1)\)计算贡献了。

由于要复制一份，满足条件的贡献至多不超过原字符串长度的一半，因此sum第二维开到一半就够了。

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 5005;

char s[N];

int main() {
    int tt;
    scanf("%d",&tt);
    while(tt--) {
        scanf("%s",s+1);
        int n = strlen(s + 1);
        vector<vector<int>> lcp(n + 2, vector<int>(n + 2));
        for (int i = n; i >= 1; i--)
            for (int j = n; j >= i; j--)
                if (s[i] == s[j]) lcp[i][j] = lcp[i + 1][j + 1] + 1;
        long long ans = 0;
        vector<vector<int>> sum(n + 1, vector<int>(n / 2 + 2));
        for (int i = 1; i < n; i++)
            for (int j = i + 1; j <= n; j++)
                if (lcp[i][j] >= j - i)
                    sum[j][j - i]++;
        for (int i = 1; i <= n; i++) {
          for (int j = 1; j <= n / 2 + 1; j++)
            sum[i][j] += sum[i][j - 1];
          for (int j = 1; j <= n / 2 + 1; j++)
            sum[i][j] += sum[i][j - 1];
        }
        for (int j = 1; j < n; j++) {
          for (int k = j + 1; k <= n; k++) {
            int len = min(lcp[j][k], k - j - 1) - 1;
            if (len >= 0) ans += sum[j][len];
          }
        }
        printf("%lld\n",ans);
    }
}