图总结

一.思维导图

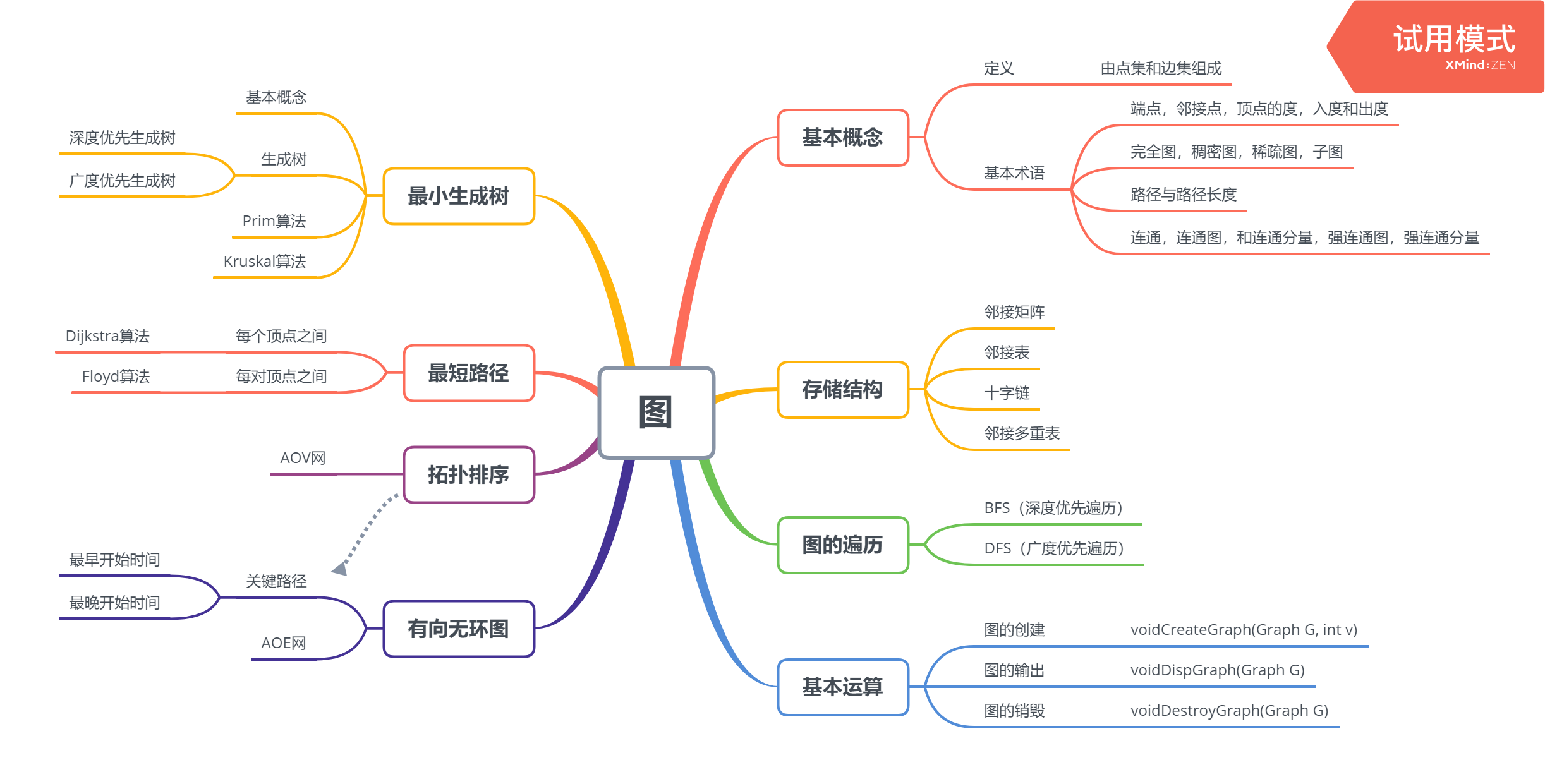
二.重要概念的笔记(不求多但求精)

1.邻接矩阵创建图

#include<iostream>
#include <string>
#include <cstdio>
#include<queue>

using namespace std;
#define MAXVEXNUM 100
//点,边
typedef  int ArcCell;
typedef char VexType;

typedef struct {
	VexType vexs[MAXVEXNUM];//点的集合
	ArcCell color[MAXVEXNUM];
	ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
	int vexNum, arcNum;
}MyGraph;

int LocateVex(MyGraph& G, VexType value)
{
	for (int i = 0; i < G.vexNum; i++)
	{
		if (G.vexs[i] == value)
		{
			return i;
		}
	}
	return -1;
}
void CreateDGraphFromConsole(MyGraph& G, int vexNum, int arcNum)
{
	int i, j;
	G.vexNum = vexNum;
	G.arcNum = arcNum;
	for (i = 0; i < vexNum; i++)
	{
		for (j = 0; j < arcNum; j++)
		{
			G.arcs[i][j] = 0;
		}
	}
	for (j = 0; j < vexNum; j++)
	{
		cin>> G.vexs[j];
	}
	for (int j = 0; j < arcNum; j++)
	{
		char x, y; ArcCell value;

		cout << "请输入x点、y点的值及x到y的边的值:" << endl;
		cin >> x; cin >> y; cin >> value;
		i1 = LocateVex(G, x);
		j1 = LocateVex(G, y);
		G.arcs[i1][j1] = value;
		G.arcs[j1][i1] = value;

	}

}

2.深度优先遍历

void DFS(MyGraph G, int v)
{
	visited[v] = 1;
	cout << G.vexs[v] << "\t";
	for (int w = 0; w < G.vexNum; w++)
	{
		if ((!visited[w]) && (G.arcs[v][w] != 0))
		{
			DFS(G, w);
		}
	}
}

3.广度优先遍历

void BFS(MyGraph G, int v)
{
	char t;
	queue<char>Q;
	cout << G.vexs[v]<<"\t";
	visited2[v] = 1;
	Q.push(G.vexs[v]);
	while (!Q.empty())
	{
		t=Q.front();
		Q.pop();
		for (int w = 0; w < G.vexNum; w++)
		{
			if (visited2[w]==0 && G.arcs[v][w] == 1)
			{
				visited2[w] = 1;
				cout << G.vexs[w]<<"\t";
				Q.push(G.vexs[w]);
				
			}
		}


	}
}

4.Prim算法构造最小生成树步骤

（1）.初始化U{v},以v到其他顶点的所有边为后选边
（2）.重复以下步骤n-1次使n-1个顶点被加入到U中

从侯选边中挑选权值最小的边加入边集TE中,让该边的顶点加入U中

考察当前所有顶点，修改后选边若当前边的权值，小于原来的侯选边，则选取当前边为侯选边.

5.Kruscal算法构造最小生成树步骤

（1）.置点集U的初值为V,边集TE为空
（2）.将图中的边按权值从小到大的顺序依次选取，若选取的边未使树形成回路，则加入边集中否则舍弃，
直到边集中有n-1条边为止。

三.疑难问题及解决方案(如果有的话，不求多但求精。可包含编程题，可只包含无解决方案的疑难问题)

图的着色问题

思路就是
对当前顶点开始着色：若当前顶点下标>n，那么就得出一个解，输出着色方案即可。否则，依次对相邻顶点，
若当前与所有其它相邻顶点无颜色冲突，则继续为下一顶点着色；否则，回溯，测试下一颜色。