csps模拟8990部分题解
题面:
666:
重点在题意转化:每个数可以乘k,代价为k,可以减一,代价为1,
所以跑最短路即可
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int MAXN=1e6+100;
int n,ans;
char f[MAXN];
bool in[MAXN];
queue<int>q;
void spfa(){
memset(f,0x3f,sizeof(f));
f[0]=1,f[1]=0;
memset(in,0,sizeof(in));
q.push(1);
in[1]=1;
while(!q.empty()){
int x=q.front();
q.pop();
if(x-1>0){
if(f[x-1]>f[x]+1){
f[x-1]=f[x]+1;
if(!in[x-1]){
in[x-1]=1;
q.push(x-1);
}
}
}
for(int i=1;i*x<=n+50&&i<=50;++i){
int y=i*x;
if(f[y]>f[x]+i){
f[y]=f[x]+i;
if(!in[y]){
in[y]=1;
q.push(y);
}
}
}
in[x]=0;
}
}
int main(){
scanf("%d",&n);
spfa();
printf("%d\n",f[n]);
return 0;
}
椎:
求treap上两点间距离
我们对所有操作离线,然后考虑把treap按中序遍历拍到序列上,这样这个序列的k是有序的
求树上两点间的距离我们套路地想到dis(x)+dis(y)-dis(lca(x,y))*2
现在就是考虑如何求dis和lca
lca好求,就是x,y区间的最大值,这个用线段树维护,维护最大值和最大值出现的位置
我们看一张图:
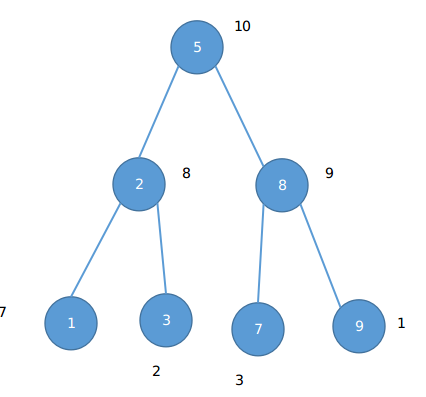
这是一个treap,圆内的是权值,外面的是优先级,我们把它拍到序列上:

不难发现求两点的lca就是区间最大值
然后考虑dis如何求,
还是线段树,观察序列我们发现一个点到根的距离就是分别以它为左右端点的上升序列,
但是注意不是最长的,我们是只要发现一个比他大的就算上,类比模拟79的T1,只要发现一个祖先智商比当前的高,就努力学习到达这个智商
比如3,2这个点,它到根的距离为2,以他为右端点的上升序列为1,以他为左端点的上升序列为1,所以总长度为2
也就是用线段树维护一个单调栈
考虑如何维护,我们已知左右区间的答案如何更新到上一个区间,
我们以向右的上升序列为例,其中左区间的贡献一定会被加进来,这时看右区间,如果右区间最大值比左区间最大值小,那么右区间没有贡献
如果右区间最大值大于左区间最大值,那么在右区间查找[lmax,rmax]的长度,然后把两段长度拼起来,这个也可以在线段树上查找
这样总复杂度$O(nlogn^2)$
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=2e5+5,inf=0x3f3f3f3f;
int n,sta[MAXN],top=0,pos[MAXN];
struct node{
int opt,k1,k2;
}a[MAXN];
struct NODE{
int maxx,lans,rans,pmx;//区间最大值,左端点最长上升,右端点最长上升,最大值的位置
}tr[MAXN<<2];
void build(int k,int l,int r){
tr[k].maxx=-inf,tr[k].pmx=-inf;
tr[k].lans=tr[k].rans=0;
int mid=(l+r)>>1;
if(l==r) return ;
build(k<<1,l,mid),build(k<<1|1,mid+1,r);
}
int askl(int k,int l,int r,int val){
if(l==r) return tr[k].maxx>val;
int mid=(l+r)>>1;
if(val>=tr[k<<1].maxx) return askl(k<<1|1,mid+1,r,val);
else return tr[k].lans-tr[k<<1].lans+askl(k<<1,l,mid,val);
}
int askr(int k,int l,int r,int val){
if(l==r) return tr[k].maxx>val;
int mid=(l+r)>>1;
if(val>=tr[k<<1|1].maxx) return askr(k<<1,l,mid,val);
else return tr[k].rans-tr[k<<1|1].rans+askr(k<<1|1,mid+1,r,val);
}
void pushup(int k,int l,int r){
if(tr[k<<1].maxx<=tr[k<<1|1].maxx)
tr[k].maxx=tr[k<<1|1].maxx,tr[k].pmx=tr[k<<1|1].pmx;
else tr[k].maxx=tr[k<<1].maxx,tr[k].pmx=tr[k<<1].pmx;
int mid=(l+r)>>1;
tr[k].lans=tr[k<<1].lans+askl(k<<1|1,mid+1,r,tr[k<<1].maxx);
tr[k].rans=tr[k<<1|1].rans+askr(k<<1,l,mid,tr[k<<1|1].maxx);
}
void update(int k,int l,int r,int opt,int val){
if(l==r){
tr[k].maxx=val,tr[k].pmx=l;
tr[k].lans=1,tr[k].rans=1;
return ;
}
int mid=(l+r)>>1;
if(opt<=mid) update(k<<1,l,mid,opt,val);
else update(k<<1|1,mid+1,r,opt,val);
pushup(k,l,r);
}
void change(int k,int l,int r,int opt){
if(l==r){
tr[k].pmx=l;
tr[k].maxx=-inf;
tr[k].lans=tr[k].rans=0;
return ;
}
int mid=(l+r)>>1;
if(opt<=mid) change(k<<1,l,mid,opt);
else change(k<<1|1,mid+1,r,opt);
pushup(k,l,r);
}
pair<int,int> query_max(int k,int l,int r,int opl,int opr){//qujianmaxx
if(opl<=l&&r<=opr) return make_pair(tr[k].maxx,tr[k].pmx);
int mid=(l+r)>>1;
pair<int,int>res=make_pair(0,0);
if(opl<=mid) res=max(res,query_max(k<<1,l,mid,opl,opr));
if(opr>mid) res=max(res,query_max(k<<1|1,mid+1,r,opl,opr));
return res;
}
pair<int,int> queryl(int k,int l,int r,int opt,int val){
if(r<=opt) return make_pair(max(val,tr[k].maxx),askr(k,l,r,val));
int mid=(l+r)>>1;
if(opt<=mid) return queryl(k<<1,l,mid,opt,val);
pair<int,int>r1,r2;
r1=queryl(k<<1|1,mid+1,r,opt,val);
r2=queryl(k<<1,l,mid,opt,max(val,r1.first));
return make_pair(r2.first,r1.second+r2.second);
}
pair<int,int> queryr(int k,int l,int r,int opt,int val){
if(l>r) return make_pair(0,0);
if(opt<=l) return make_pair(max(val,tr[k].maxx),askl(k,l,r,val));
int mid=(l+r)>>1;
if(opt>mid) return queryr(k<<1|1,mid+1,r,opt,val);
pair<int,int>r1,r2;
r1=queryr(k<<1,l,mid,opt,val);
r2=queryr(k<<1|1,mid+1,r,opt,max(val,r1.first));
return make_pair(r2.first,r1.second+r2.second);
}
int dis(int x){
int res=(x==1)?0:queryl(1,1,top,x-1,pos[x]).second;
return res+queryr(1,1,top,x+1,pos[x]).second;
}
int query(int x,int y){
return dis(x)+dis(y)-2*dis(query_max(1,1,top,x,y).second);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&a[i].opt);
if(a[i].opt==0){
scanf("%d%d",&a[i].k1,&a[i].k2);
sta[++top]=a[i].k1;
}else if(a[i].opt==1){
scanf("%d",&a[i].k1);
}else{
scanf("%d%d",&a[i].k1,&a[i].k2);
}
}
sort(sta+1,sta+top+1);
top=unique(sta+1,sta+top+1)-sta-1;
build(1,1,top);
for(int i=1;i<=n;++i){
if(a[i].opt==0){
int p=lower_bound(sta+1,sta+top+1,a[i].k1)-sta;
update(1,1,top,p,a[i].k2);
pos[p]=a[i].k2;
}else if(a[i].opt==1){
int p=lower_bound(sta+1,sta+top+1,a[i].k1)-sta;
change(1,1,top,p);
pos[p]=-inf;
}else{
int p1=lower_bound(sta+1,sta+top+1,a[i].k1)-sta;
int p2=lower_bound(sta+1,sta+top+1,a[i].k2)-sta;
if(p1>p2) swap(p1,p2);
printf("%d\n",query(p1,p2));
}
}
return 0;
}
新的世界:
考场成功理解错题意,以为一个光源只能被经过一次
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define int long long
using namespace std;
const int MAXN=505;
int n,m,a[MAXN][MAXN],dis[MAXN][MAXN],r,c,l,P,Q;
bool in[MAXN][MAXN];
int dx[4]={-1,0,0,1};
int dy[4]={0,-1,1,0};
queue<pair<int,int> >que;
void spfa(int x,int y){
que.push(make_pair(x,y));
memset(dis,0x3f,sizeof(dis));
dis[x][y]=0,in[x][y]=1;
while(!que.empty()){
x=que.front().first,y=que.front().second;
que.pop();
for(int i=0;i<4;++i){
int p=x+dx[i],q=y+dy[i];
if(p<1||p>n||q<1||q>m) continue;
if(dis[p][q]>dis[x][y]+a[p][q]){
dis[p][q]=dis[x][y]+a[p][q];
if(!in[p][q]){
que.push(make_pair(p,q));
in[p][q]=1;
}
}
}
in[x][y]=0;
}
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)
scanf("%lld",&a[i][j]);
}
scanf("%lld%lld%lld%lld%lld",&r,&c,&l,&P,&Q);
spfa(r,c);
/*for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
cout<<dis[i][j]<<' ';
}
cout<<endl;
}*/
printf("%lld\n",max(0ll,l-dis[P][Q]));
return 0;
}
光线追踪:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号