深入理解SVM之对偶问题
我是搬运工:http://my.oschina.net/wangguolongnk/blog/111349
1. 支持向量机的目的是什么?
对于用于分类的支持向量机来说,给定一个包含正例和反例(正样本点和负样本点)的样本集合,支持向量机的目的是寻找一个超平面来对样本进行分割,把样本中的正例和反例用超平面分开,但是不是简单地分看,其原则是使正例和反例之间的间隔最大。
超平面是什么呢?简单地说,超平面就是平面中的直线在高维空间中的推广。那么,对于三维空间,超平面就是平面了。对于更高维的空间,我们只能用公式来表达,而缺少直观的图形了。总之,在n维空间中的超平面是n-1维的。
超平面的公式为![]() 。公式中的w为可以调整的系数向量,b为bias。注意我们的表达习惯,所有的向量都是列向量,所以在第一项的内积中向量w需要进行转置。
。公式中的w为可以调整的系数向量,b为bias。注意我们的表达习惯,所有的向量都是列向量,所以在第一项的内积中向量w需要进行转置。
现在考虑样本集合{xi,di},xi是输入的特征,di是样本对应的分类。现在规定当样本xi属于第一类时,di为1,当xi属于第二类时,di为-1。
那么,线性可分的意思就是一个超平面可以把两类样本完全地分割开来。用公式表达就是:
你现在可能会问,那么如果不是线性可分的情况应该怎么办呢?事实是这些会在后面处理到。在这里我们首先讨论线性可分的情况,然后将其拓展到线性不可分的情况.
现在假设对于线性可分的样本集,我们有了一个分割超平面![]() ,现在我们想通过调整w0和b0让它分割的正样本和负样本保持最大的间隔,这样我们就获得了最优的超平面。实际上在操作过程中,我们最大化的是离超平面最近的点到超平面的距离。也就是说,我们要让超平面尽量远离最近的点。从图中可见超平面到正样本最近点的距离和超平面到负样本最近点的距离是相等的。这是个巧合么?
,现在我们想通过调整w0和b0让它分割的正样本和负样本保持最大的间隔,这样我们就获得了最优的超平面。实际上在操作过程中,我们最大化的是离超平面最近的点到超平面的距离。也就是说,我们要让超平面尽量远离最近的点。从图中可见超平面到正样本最近点的距离和超平面到负样本最近点的距离是相等的。这是个巧合么?
假 设我们已经找到了一个超平面,它离正样本最近点的距离大于离负样本最近点的距离,那么这个离超平面最近的点就是负样本中的最近点。而考虑到我们的目标,我 们还会调整超平面的位置使它还可以增大一些,即使这样会牺牲离正样本最近点的距离。所以调整到最后的结果肯定是超平面离两侧最近点的距离是等距的。
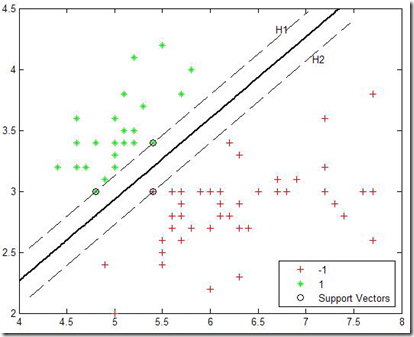
为了更形象地表现正负样本的间隔,我们可以在分割超平面的两侧再定义两个超平面H1和H2(如图中虚线所示),这两个超平面分别通过正样本和负样本中离分割超平面最近的样本点(图中加了外圈)。从以上分析可以知道,超平面H1和H2离分割超平面是等距的。
我们定义超平面H1和H2上面的点叫做支持向量。正负样本的间隔可以定义为超平面H1和H2之间的间隔,它是分割超平面距最近正样本点距离和最近负样本点距离之和。
从 图中可以看出,支持向量对于分割超平面的位置是起到关键作用的。在优化分割超平面位置之后,支持向量也显露出来,而支持向量之后的样本点则对分类并不关 键。为什么这样说呢?因为即使把支持向量以外的样本点全部删除,再找到最优的分割超平面,这个超平面的位置跟原先的分割超平面的位置也是一样的。总结起来 就是:
支持向量包含着重构分割超平面所需要的全部信息!
2. 样本点到超平面距离的表示
如何求一点到超平面的距离呢?
现在我们来看看系数向量w0是什么含义?回忆一下,w0实际上是超平面的法向量!
那么,对于任意一个样本点x,它可以表示为:
其中xp是x在超平面上的投影,r是x到超平面的几何距离(几何间隔)。
现在我们开看,g(x)实际上度量了样本点x到超平面的距离,在||w0||恒定的情况下,g(x)绝对值的大小反映了几何间隔r的大小。我们给g(x)起个名字叫做函数间隔。注意几何间隔r和函数间隔g(x)都是有正负号的,代表着处于超平面的不同侧。
3. 最大化间隔
我们已经知道了函数间隔和几何间隔的表示,现在回到正题,我们需要最大化支持向量到分割超平面的距离,当然在最开始我们不知道哪些向量是支持向量。
我们的目的是最大化支持向量到分割超平面的几何间隔r,而不是最大化函数间隔g(x),为什么呢?因为超平面方程的系数可以同比例增大或者减小,而不改变超平面本身。所以||w0||是不固定的,这就会影响函数间隔g(x)的大小。
所以我们需要最大化的是几何间隔r,这等价于我们固定||w0||,然后最大化函数间隔g(x)。但是实际上我们不会这么做,通常的处理方法是固定函数间隔g(x)的绝对值为1,然后最小化||w0||。也就是说我们把支持向量到分割超平面的函数间隔g(x)的绝对值设定为1,然后最小化||w0||。
4. 正式的表述
现在我们可以正式地表述这个问题了。我们需要最小化||w0||,也就是最小化超平面权重向量w0的欧几里得范数。但是有没有限定条件呢?还记得上一节最后一句话么?
“也就是说我们把支持向量到分割超平面的函数间隔g(x)设定为1,然后最小化||w0||”
所以最小化||w0|| 是有限定条件的,如何表述限制条件呢?我们把支持向量对应的g(x)定为+1或者-1(取决于支持向量处于分割超平面的哪一侧,也就是说是正样本还是负样 本),也就表明了对于所有的正样本点来说,g(x)是>=+1的,而对于负样本来说,g(x)是<=-1的。
回想g(x)的定义:
我们可以把限制条件写下来:
现在我们可以把上面的问题写的更简练:
目标函数:
限制:
1/2是为了以后计算方便所加的,N是样本点的个数。
现在我们的第一个任务结束了,我们把要寻找最优的分割超平面的问题转化为带有一系列不等式约束的优化问题。这个最优化问题被称作原问题。我们不会直接解它,而是把它转化为对偶问题进行解决。至于如何将其转化为对偶问题,这是以后几节的内容。
对支持向量机的求解都是将上节说的原问题转化为对偶问题进行求解的,这些内容都是最优化课程中的内容。
回忆上节的内容,我们的目标是寻找函数在若干约束条件下的最小值。在上节的原问题中,约束条件是包含不等式的,本节先考虑简单的问题,即考虑只包含等式约束的最优化问题:
其中f(x)被称作目标函数,而下面是一系列的等式约束。回想一下,当没有任何约束存在的时候,应该怎样寻找最优点呢?事实上x*是最优点的必要条件是:
而如果函数f(x)是凸函数的话,这个条件也是充分条件。
插入一个说明,如果函数f(x)是一个实值函数,x是一个n维向量,那么f(x)对向量x的导数被定义为:
回到目前的问题,当我们寻找约束存在时的最优点的时候,约束的存在虽然减小了需要搜寻的范围,但是却使问题变得更加复杂。为了使问题变得易于处理,我们的方法是把目标函数和约束全部融入一个新的函数,即拉格朗日函数,再通过这个函数来寻找最优点。
为了形象化地分析这个问题,我们考虑目标函数是三变量的函数并且只有一个约束的情况:
从几何上来看,上面的问题(2)就是从曲面![]() 上来寻找函数
上来寻找函数![]() 的最小值。假设问题(2)的最优解是
的最小值。假设问题(2)的最优解是![]() 。我们现在做曲面Ω上任一条通过点x的光滑曲线l:
。我们现在做曲面Ω上任一条通过点x的光滑曲线l:![]() (由于曲线l是在曲面Ω上的,所以自然有
(由于曲线l是在曲面Ω上的,所以自然有![]() )。
)。
令最优点![]() 对应的t为t*。因为x*是曲面Ω上的最优点,所以x*也是曲线l上的最优点,所以t*是一元函数
对应的t为t*。因为x*是曲面Ω上的最优点,所以x*也是曲线l上的最优点,所以t*是一元函数![]() 的最优点,所以在这一点它的导数是0。通过链式法则我们得到:
的最优点,所以在这一点它的导数是0。通过链式法则我们得到:
这个式子说明了在x*这一点,函数![]() 的梯度向量
的梯度向量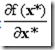 和曲线l在x*处的切线是垂直的。由于曲线l是任意的,所以梯度向量
和曲线l在x*处的切线是垂直的。由于曲线l是任意的,所以梯度向量 和曲面Ω是垂直的。
和曲面Ω是垂直的。
回忆高等数学的结论,![]() 的方向就是曲面Ω的法线方向,所以
的方向就是曲面Ω的法线方向,所以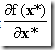 和
和![]() 必然在同一直线的方向上,所以必定存在一个常数μ*,有
必然在同一直线的方向上,所以必定存在一个常数μ*,有![]() 。
。
我们可以把它写成更加精炼的形式。如果我们构造二元函数![]() ,上面的结论就可以表达为必定存在着常数μ*,使
,上面的结论就可以表达为必定存在着常数μ*,使![]() 。
。
我们把构造的函数![]() 称作拉格朗日函数,而其中的μ称作拉格朗日乘子。
称作拉格朗日函数,而其中的μ称作拉格朗日乘子。
关于只有等式约束的拉格朗日函数的引入,也可以参考维基百科中的两个变量函数的例子。
以上是一个特殊情形的分析,并且只包含了一个约束。那么包含等式约束的一般情况,也就是问题(1)来说,我们同样可以构造拉格朗日函数,不过由于包括多个等式约束,表达稍微不同:
也就是说,每一个等式约束都对应着一个拉格朗日乘子。那么x*是最优点的必要条件就是,存在相应的拉格朗日乘子μ*,使得以下两个式子成立:
这两个式子就是最优点的必要条件,当然如果函数![]() 是凸函数的话,这两个式子也是充分条件。
是凸函数的话,这两个式子也是充分条件。
现在我们的目标达到了,也就是把目标函数和一系列的等值约束融合到了一个函数(拉格朗日函数)里面,这样只需要解(3)和(4)这两个式子就可以找到最优点,其优点是不言而喻的。而在下一节中我们将会讨论包含不等式约束的最优化问题。
我们首先要引入包含不等式约束的优化问题,标准形式如下:
f(x)是目标函数,而后面分别是一系列的不等式约束和等式约束。
我们首先明确几个概念:
可行点(可行解):所有满足约束的点x。
可行域:所有可行点组成的点集,记为R。正式写出来就是:
最优点(最优解):满足约束(也就是处于可行域之内)并且使目标函数达到最小的点,记为x*。
最优值:如果找到了x*,p* = f(x*) 就是最优值。
明确了这些概念以后我们就接着说下面的内容了。
与上节所说的只包含等式约束的情况类似,我们定义拉格朗日函数如下:
我们来看看,这与上节的拉格朗日函数有什么不同?多了一系列的不等式约束对应的项,所以也多了一系列的拉格朗日乘子。在这里需要强调的是,所有的λi必须是大于等于0的(也即是不等式约束对应的乘子要求大于等于0,我们记为λ≥0,意思是每个都λi≥0)。至于为什么要这样要求,后面自然可以看出来。
接下来我们定义一个重要的函数,我们定义拉格郎日对偶函数(the Lagrange dual function)如下:
所以拉格朗日对偶函数![]() 就是把
就是把![]() 看成x的函数所找到的最小值。找到这个最小值有什么意义呢?
看成x的函数所找到的最小值。找到这个最小值有什么意义呢?
我们先把结论写下来,这个结论十分重要,是本节论述的目的:
对偶函数![]() 产生了原问题(1)最优值p*的一个下界,也就是说,对于任意的λ≥0和任意的μ来说,有:
产生了原问题(1)最优值p*的一个下界,也就是说,对于任意的λ≥0和任意的μ来说,有:
那么如何证明(3)呢?
这个证明步骤十分简洁。假设x*是原问题(1)中的最优解,也就是f(x*) = p*。
最后两行的推导是考虑到x*是在可行域R内的,所以肯定有![]() ,当然前提是λ≥0,这也就是为什么在一开始要做这个规定的原因了。
,当然前提是λ≥0,这也就是为什么在一开始要做这个规定的原因了。
我们如何理解这个不等式(3)呢?下面给出两个直观的解释:
解释一:线性逼近的解释
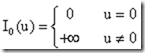
我们首先重写问题(1),就是把问题(1)换个更加紧凑的方式来表达,首先我们定义示性函数:
同样我们也可以定义另外一个示性函数:
有了这两个示性函数的帮助,现在我们可以把问题(1)重新写成一个没有约束的形式:
我们来看看这个优化问题(4)和问题(1)是等价的么?我们可以把(4)的后面两大项看做是对违反约束条件的x的惩罚函数。![]() 起的作用是对违反不等式约束的x进行“无限的”惩罚,也就一旦
起的作用是对违反不等式约束的x进行“无限的”惩罚,也就一旦![]() ,惩罚就等于无穷大。而
,惩罚就等于无穷大。而![]() 起的作用是对违反等式约束的x进行惩罚,一旦
起的作用是对违反等式约束的x进行惩罚,一旦![]() ,惩罚就为无穷大。这样对(4)中目标函数的优化跟对(1)中目标函数在约束条件下的优化就是同一回事,是不是?也就是说,(1)和(4)这两个问题是等价的问题,但是在(4)中约束被融合到目标函数中来了。
,惩罚就为无穷大。这样对(4)中目标函数的优化跟对(1)中目标函数在约束条件下的优化就是同一回事,是不是?也就是说,(1)和(4)这两个问题是等价的问题,但是在(4)中约束被融合到目标函数中来了。
现在我们再回头看看(2),也就是拉格朗日对偶函数![]() ,它也是个优化问题,我们对比它所优化的函数和(4)中所优化的函数,把它们重写在一起:
,它也是个优化问题,我们对比它所优化的函数和(4)中所优化的函数,把它们重写在一起:
可见在问题(2)和问题(4)中,我们优化的目标函数区别在于惩罚项不同,(4)中的惩罚项是无限的,就是说一旦违反约束,就施加无穷大的惩罚;而在(2)中我们的惩罚项是线性的,就是说随着gi(x)和hi(x)的不同,惩罚项是线性变化的。所以(2)和(4)中需要优化的目标函数有很大的不同,用(2)来逼近(4)是很不准确的。但是我们可以看出,对于任意的u,任意的λ≥0和任意的μ来说都有:
所以在任意点,(2)中的目标函数的值都是小于(4)中的目标函数的值,所以(2)中找到的最优值肯定是小于(4)中找到的最优值的。再结合前面说的(1)和(4)是等价的问题,所以不等式(3)是成立的。
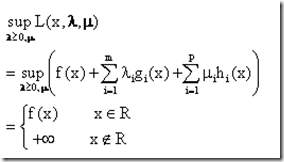
解释二:交换max和min的次序
我们首先可以看出:
为什么会有这个结果呢?当x满足约束的时候,也就是对所有的i来说有 并且
并且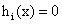 ,如果我们想通过调整λ和μ让
,如果我们想通过调整λ和μ让 变大怎么办呢?只有让λ全部为0(注意λ只能大于等于0),这样就消去了小于0的项,至于
变大怎么办呢?只有让λ全部为0(注意λ只能大于等于0),这样就消去了小于0的项,至于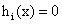 ,无论μ怎么变都是没有影响的。所以当x属于可行域的时候上式的结果是f(x)。如果x违反了约束呢?在做sup运算的时候只需要对满足
,无论μ怎么变都是没有影响的。所以当x属于可行域的时候上式的结果是f(x)。如果x违反了约束呢?在做sup运算的时候只需要对满足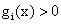 和
和 的项对应的乘子定为+∞,而把其他的项对应的乘子设为0,就可以让整个式子的结果变为无穷大。
的项对应的乘子定为+∞,而把其他的项对应的乘子设为0,就可以让整个式子的结果变为无穷大。
所以我们可以看出来,在问题(1)中的带约束的优化问题和直接优化 是一回事,也就是说:
是一回事,也就是说:
现在我们把inf和sup两个运算符调换次序,显然有:
我们重写(2)式:
可以看出结论了,也就是λ≥0时(3)式成立:
好了,费了半天的劲我们说明了一个问题,就是不等式(3)是怎么来的。
总结一下,不等式(3)用文字叙述就是:
如果我们把拉格朗日函数看做是x的函数,然后取下确界(注意:是在整个定义域里取下确界,而不是仅仅在可行域里取值,也就是说取下确界时对x是没有约束的),那么得到的结果就是原优化问题(1)的最优值的一个下界。
至于我们得到这个结果有什么用,下节再说。
回忆上一节,对如下的原问题:
我们定义了拉格朗日对偶函数:
也就是说我们找到了原问题最优值的一个下界。既然我们找到了一个下界,显然我们要找到它最好的下界。什么是最好的下界的?显然就是所有下界当中最大的那一个。所以我们要把 最大化,当然我们还要记得我们需要限制
最大化,当然我们还要记得我们需要限制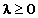 。我们把要优化的函数和约束条件正式写下来就是:
。我们把要优化的函数和约束条件正式写下来就是:
与原问题(1)相对应,我们把上面的问题(2)称作拉格朗日对偶问题(Lagrange dual problem)。显然,对偶问题的最优值d*就是我们可以获得的p*的最优下界,也就是所有下界中离p*最近的一个,它们的关系是:
我们把这个不等式叫做弱对偶性质(Weak Duality)。
顺其自然,我们可以引出一个重要的概念,对偶间隙,其定义为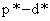 ,用文字叙述就是原问题的最优值与通过拉个郎日对偶函数获得的其最好(最大)的下界之差。由不等式(3)可以看出,对偶间隙肯定是大于等于0的。
,用文字叙述就是原问题的最优值与通过拉个郎日对偶函数获得的其最好(最大)的下界之差。由不等式(3)可以看出,对偶间隙肯定是大于等于0的。
那么有没有可能在某种情况下,对偶间隙消失了呢?也就是说对偶问题的最优值与原问题的最优值相等了呢?
我们将要叙述一下Slater条件:
Slater条件:
Slater条件即是说存在x,使不等式约束中的“小于等于号”要严格取到“小于号”。
可以证明,对于凸优化问题(关于凸优化问题,请参考维基百科),如果Slater条件满足了,则:
这种情况称为强对偶性质(Strong Duality)。
下面的问题是,如果对偶间隙消失了,会发生什么有趣的现象呢?
如果对偶间隙消失了,也就是说,如果对偶问题存在着最优点λ*,μ*并且使其对应的最优值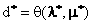 等于p*,这时会发生什么情况呢?还记得上一节我们证明
等于p*,这时会发生什么情况呢?还记得上一节我们证明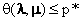 的过程么:
的过程么:
在对偶间隙消失的情况下,中间所有的不等号都要变成等号:
注意,(5)中的λ和μ都加了星号,表示它们是对偶问题的最优点。(5)中有两个重要的等号,已经加了标记。
我们能得出什么结论?
1 .我们先来看等号1:
2. 我们再来看等号2:
它说明了:
由于我们限制了每一个λi≥0,所以上式中每一项都是非正的。这样我们又可以得出结论:
等式(6)被称作是互补性条件,我们可以把它换种写法:
或者写成它的等价形式(逆否命题):
也就是说,只要一个不为0,另一个就必为0!
互补性条件有着重要的意义。它说明了当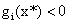 时,x*是处于可行域的内部的,这时不等式约束并不起作用,此时
时,x*是处于可行域的内部的,这时不等式约束并不起作用,此时 ;而
;而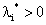 的点肯定是可行域边界的点(
的点肯定是可行域边界的点(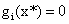 )。也就是说只有积极约束才有不为0的对偶变量。而这在支持向量机中有着重要的意义。回想在第一节我们最后的结论,支持向量机寻找最大间隔超平面可以归结为一个优化问题:
)。也就是说只有积极约束才有不为0的对偶变量。而这在支持向量机中有着重要的意义。回想在第一节我们最后的结论,支持向量机寻找最大间隔超平面可以归结为一个优化问题:
目标函数:
限制:
那么哪些不等式约束对应着不为0的对偶变量呢?显然,只有当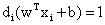 时,这个约束对应的对偶变量才可能不为0,而
时,这个约束对应的对偶变量才可能不为0,而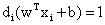 意味着什么?意味着这个约束对应的样本点xi是支持向量!也就是说:
意味着什么?意味着这个约束对应的样本点xi是支持向量!也就是说:
只有支持向量才对应不为0的拉格朗日乘子!

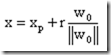
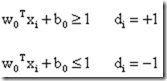
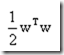
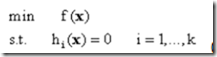

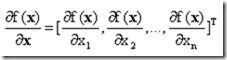
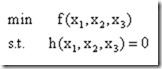
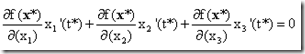
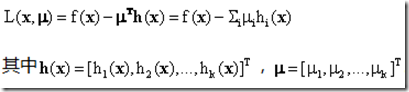
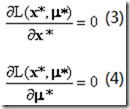
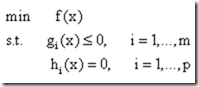
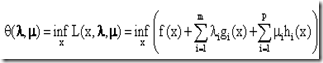
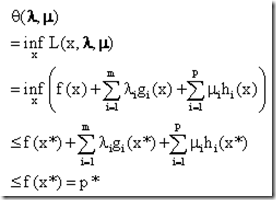
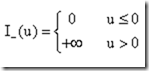

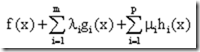



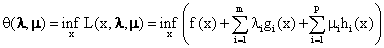
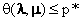
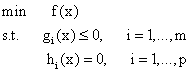

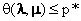
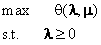
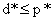
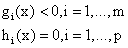
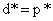
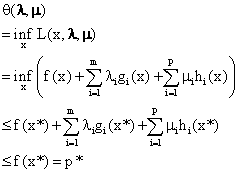
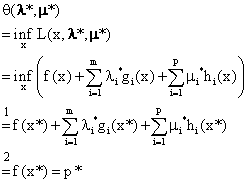
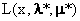
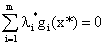
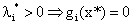
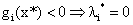

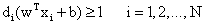


 浙公网安备 33010602011771号
浙公网安备 33010602011771号