第二册 三角函数，数列

三角函数

1. 任意角的三角函数

1. 任意角

选定一个平面，一条射线绕它的端点旋转有两个相反的方向：顺时针和逆时针。由一条射线绕其端点旋转而生成的角，通常叫做转角。规定：

  1. 按逆时针方向旋转而来的角叫正角；按逆时针旋转而成的角叫负角；当射线没有旋转时，称为零角。
  2. 当射线绕其端点旋转时，旋转的绝对量可以是任意的，于是便有任意角，包括上述的三种角。在画图时，常用带箭头的弧线来表示旋转的方向和绝对量。About This.
    我们通常在平面直角坐标系内讨论角。为了方便，我们使教的顶点与坐标原点重合，角的始边与 \(x\) 轴的非负半轴重合。那么，角的终边在第几象限，就称这个角是第几象限角，如 \(-30^{\circ}\) 是第四象限角，\(120^{\circ}\) 是第二象限角。特别的，若一个角的终边在坐标轴上，则这个角不是象限角。
  3. "\(0^{\circ}\)~ \(90^{\circ}\)的角"指的是"满足 \(0^{\circ}\le\alpha<90^{\circ}\) 的角 \(\alpha\) ”。

2. 弧度制

前面所用的角度作为角的大小的度量单位，\(1^{\circ}\) 的角等于周角的 \(\frac{1}{360}\)，这种叫做角度制；还有另一种单位制，弧度制。
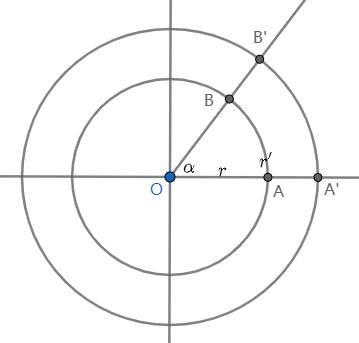
image

如图所示，由于对同一个圆心角 \(\alpha\) 而言，它所对的弧和相应的圆的半径之比是一个定值，即 \(\frac{\overset{\frown}{AB}}{r}=\frac{\overset{\frown}{A'B'}}{r'}\)。这个比值由角 \(\alpha\) 的大小决定，和其所在圆没有关系。可以用弧长和相应半径的比值来度量角度。

把长度等于半径长的圆弧所对的圆心角叫做 \(1\)弧度 的角，用符号 \(\operatorname{rad}\) 表示，读作弧度。

一般地，正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是 \(0\)。如果半径为 \(r\) 的圆的圆心角 \(\alpha\) 所对的弧长为 \(l\)，那么，角 \(\alpha\) 的弧度数的绝对值是 \(|\alpha|=\frac{l}{r}\)。

由于周角在角度制下的度量值是 \(360^{\circ}\)，在弧度制下的度量值是 \(2 \pi\)，所以 \(360^{\circ}=2\pi\)，于是得到角度制和弧度制的转化关系：

\[\begin{cases}1^{\circ}=\frac{\pi}{180}\operatorname{rad}\approx0.01745\operatorname{rad}\\1\operatorname{rad}=\left(\frac{180}{\pi}\right)^{\circ}\approx57.30^{\circ}\end{cases}\\ \]

在用弧度制表示角时，“弧度”二字或符号 \(\operatorname{rad}\) 通常略去不写，只写出该角对应的弧度数

3. 任意角三角函数的定义

设 \(\alpha\) 是一个角，使角 \(\alpha\) 顶点与坐标原点重合，始边与 \(x\) 轴非负半轴重合，任取 \(\alpha\) 上的异于原点的任意一点 \(P(x,y)\)，记 \(r=\left|\overrightarrow{OP}\right|=\sqrt{x^2+y^2}\)，
定义：

  • \(\frac{x}{r}\) 叫做角 \(\alpha\) 的余弦，记作 \(\cos\alpha\)，即 \(\cos\alpha=\frac{x}{r}\)；
  • \(\frac{y}{r}\) 叫做角 \(\alpha\) 的正弦，记作 \(\sin\alpha\)，即 \(\sin\alpha=\frac{y}{r}\)；
  • \(\frac{y}{x}\) 叫做角 \(\alpha\) 的正切，记作 \(\tan\alpha\)，即 \(\tan\alpha=\frac{y}{x}(x \not=0)\)；

由上可得，对于每个确定的角 \(\alpha\)，都有唯一的余弦值、正弦值与之对应，当 \(\alpha\not=k\pi+\frac{\pi}{2}(k\in\Bbb{Z})\) 时有唯一的正切值与之对应。这几个函数都是三角函数，它们的定义域和正负如表格所示。

4、单位圆和三角函数线

设 \(\alpha\) 是一个角，点 \(P(x,y)\) 是 \(\alpha\) 的终边与单位圆（以原点为圆心，半径为 \(1\) 的圆）的交点，则 \(r=\left|\overrightarrow{OP}\right|=1\)，于是有 \(x=\cos\alpha,y=\sin\alpha\)。就是说，角 \(\alpha\) 的余弦和正弦分别等于角 \(\alpha\) 终边与单位圆交点的横坐标与纵坐标。
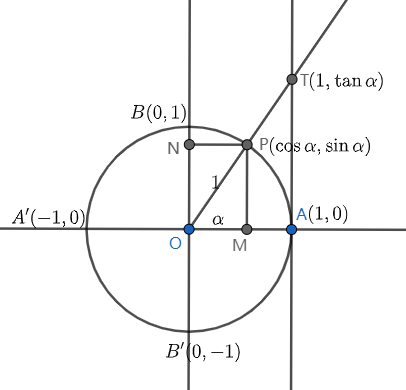
image
设 \(\alpha\) 为一个角，点 \(P(x,y)\) 是 \(\alpha\) 的终边与单位圆的交点，将 \(\overrightarrow{OP}\) 沿 \(x,y\) 轴方向分解得 \(\overrightarrow{OP}=\overrightarrow{OM}+\overrightarrow{ON}\)，其中点 \(M,N\) 分别位于 \(x\) 轴和 \(y\) 轴上，把有向线段 \(\overrightarrow{OM},\overrightarrow{ON}\) 分别称为角 \(\alpha\) 的余弦线和正弦线，则 \(\overrightarrow{OM}=(\cos\alpha,0),\overrightarrow{ON}=(0,\sin\alpha)\)。

设直线 \(OP\) 与直线 \(x=1\) 的交点为 \(T\)，则 \(T(1,\tan\alpha)\)，把有向线段 \(\overrightarrow{AT}\) 称为角 \(\alpha\) 的正切线，则 \(\overrightarrow{AT}=(1,\tan\alpha)\)。

5. 特殊角三角函数

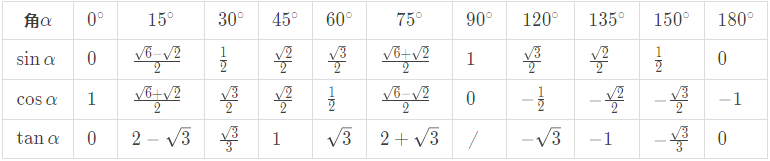
image

2.同角三角函数关系与诱导公式

1. 同角三角函数的基本关系

设 \(\alpha\) 是一个角，根据三角函数的定义，可得

\[\sin^2\alpha+\cos^2\alpha=1,\tan\alpha=\frac{\sin\alpha}{\cos\alpha} \]

\(\sin\alpha,\cos\alpha,\tan\alpha\) 知一求二。

2. 诱导公式

  1. 角 \(\alpha\) 与角 \(\alpha+2k\pi,k\in\Bbb{Z}\) 的三角函数的关系

\[(1)\begin{cases}\sin(\alpha+2k\pi)=\sin\alpha\\\cos(\alpha+2k\pi)=\cos\alpha\\\tan(\alpha+2k\pi)=\tan\alpha\\\end{cases}\\ \]

  1. 角 \(\alpha\) 与角 \(-\alpha\) 的三角函数的关系

\[(2)\begin{cases}\sin(-\alpha)=-\sin\alpha\\\cos(-\alpha)=\cos\alpha\\\tan(-\alpha)=-\tan\alpha\\\end{cases}\\ \]

  1. 角 \(\alpha\) 与角 \(\alpha+(2k+1)\pi,k\in\Bbb{Z}\) 的三角函数的关系

\[(3)\begin{cases}\sin(\alpha+(2k+1)\pi)=-\sin\alpha\\\cos(\alpha+(2k+1)\pi)=-\cos\alpha\\\tan(\alpha+(2k+1)\pi)=\tan\alpha\\\end{cases}\\ \]

  1. 角 \(\alpha\) 与角 \(\pi-\alpha\) 的三角函数的关系

\[(4)\begin{cases}\sin(\pi-\alpha)=\sin\alpha\\\cos(\pi-\alpha)=-\cos\alpha\\\tan(\pi-\alpha)=-\tan\alpha\\\end{cases}\\ \]

  1. 角 \(\alpha\) 与角 \(\frac{\pi}{2}-\alpha\) 的三角函数的关系

\[(5)\begin{cases}\sin(\frac{\pi}{2}-\alpha)=\cos\alpha\\\cos(\frac{\pi}{2}-\alpha)=\sin\alpha\\\end{cases}\\ \]

  1. 角 \(\alpha\) 与角 \(\frac{\pi}{2}+\alpha\) 的三角函数的关系

\[(6)\begin{cases}\sin(\frac{\pi}{2}+\alpha)=\cos\alpha\\\cos(\frac{\pi}{2}+\alpha)=-\sin\alpha\\\end{cases}\\ \]

公式 \((1)\)~\((6)\) 统称为诱导公式。

  1. 余切函数
    设 \(\alpha\) 是一个角，则 \(f(\alpha)=\frac{\cos\alpha}{\sin\alpha}\) 称为角 \(\alpha\) 的余切函数，记作 \(\cot\alpha\)，显然，\(\tan\alpha·\cot\alpha=1\)。
    有：\(\tan(\frac{\pi}{2}-\alpha)=\cot\alpha,\cot(\frac{\pi}{2}-\alpha)=\tan\alpha,\tan(\frac{\pi}{2}+\alpha)=-\cot\alpha,\cot(\frac{\pi}{2}-\alpha)=-\tan\alpha\)

“奇变偶不变，符号看象限。”

3. 三角函数的图像与性质

1. 正弦函数的图像

正弦函数具有 有界性和周期性。
利用特殊标，采用描点法，可以得到正弦函数 \(y=\sin x\) 在 \([0,2\pi]\) 内的图像：
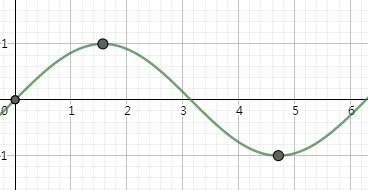
image
因为 \(\sin(x+k·2\pi)=\sin x,k\in\Bbb{Z}\) ，所以把如上图像平移可得 \(y=\sin x,x\in\Bbb{R}\) 的图像：
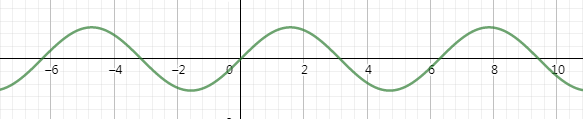
image
此图像称为正弦曲线

2.正弦函数的性质

  1. 值域
    正弦函数的值域是 \([-1,1]\)。当且仅当 \(x=2k\pi+\frac{\pi}{2},k\in\Bbb{Z}\) 时取最大值 \(1\)；\(x=2k\pi-\frac{\pi}{2},k\in\Bbb{Z}\) 时取最小值 \(-1\)。
  2. 周期性
    正弦函数是一个周期为 \(2k\pi\) 的周期函数，其中， \(2\pi\) 是其最小正周期，对于三角函数，一般把最小正周期简称为周期。
  3. 奇偶性
    正弦函数是奇函数，关于原点对称。
  4. 单调性
    正弦函数在区间 \(\left[2k\pi-\frac{\pi}{2},2k\pi+\frac{\pi}{2}\right],k\in\Bbb{Z}\) 上递增；在区间 \(\left[2k\pi+\frac{\pi}{2},2k\pi+\frac{3\pi}{2}\right],k\in\Bbb{Z}\) 上递减。\(x=k\pi,k\in\Bbb{Z}\) 是其零点。

3.余弦函数的图像和性质

图像如下：
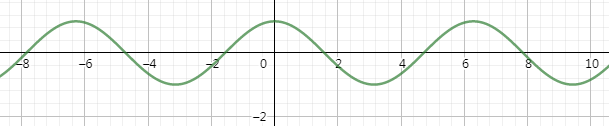
image
余弦函数是偶函数，图像关于 \(y\) 轴对称。余弦函数是一个周期为 \(2k\pi\) 的周期函数，在区间 \(\left[(2k+1)\pi,2(k+1)\pi\right],k\in\Bbb{Z}\) 上递增；在区间 \(\left[2k\pi,(2k+1)\pi\right],k\in\Bbb{Z}\) 上递减。\(x=k\pi+\frac{\pi}{2},k\in\Bbb{Z}\) 是其零点。

4. 三角函数的图像变换

  1. 平移变换
    1. 左右平移
      \(y=\sin x \to y=\sin(x+\varphi)\)，\(\varphi>0\) 向左平移 \(\varphi\) 单位，反之向右平移 \(|\varphi|\) 个单位。
    2. 上下平移
      \(y=\sin x\to y=\sin x+k\)，\(k>0\) 向上平移 \(k\) 个单位，反之向下平移。
    3. 周期变换
      \(y=\sin x\to y=\sin\omega x\)，纵坐标不变，横坐标变为为原来的 \(\frac{1}{\omega}\) 倍。
    4. 振幅变换
      \(y=\sin x\to y=A\sin x\)，横坐标不变，纵坐标变为原来的 \(A\) 倍。

注意：参数只影响函数中的自变量，不影响其中的常数。
例： \(y=\sin(x+2)\to y=\sin(2x+2)\) 把原函数的横坐标变为了原来的 \(\frac{1}{2}\) 倍，\(y=\sin((\cos x)+2)\to y=\sin(\cos(2x)+2)\) 同理。

5. 正弦型函数

形如 \(y=A\sin(\omega x+\varphi)\)（其中，\(A,\omega,\varphi\) 都是常数）的函数，叫做正弦型函数。一般地，对正弦函数，我们有：

  1. \(A\) 称为 \(y=A\sin(\omega x+\varphi)\) 的振幅，指函数曲线在纵坐标上的波动幅度。
  2. \(\varphi\) 称为 \(y=A\sin(\omega x+\varphi)\) 的初相,\(\omega x+\varphi\) 称为它的相位。对称轴为 \(\omega x+\varphi=k\pi+\frac{\pi}{2}\)，对称轴的横坐标 \(x\) 满足 \(\omega x+\varphi=k\pi\)。
  3. \(\omega\) 称为 \(y=A\sin(\omega x+\varphi)\) 的角速度，若 \(\omega\not=0\)，则其周期为 \(T=\frac{2\pi}{|\omega|}\)，\(f=\frac{1}{T}=\frac{|\omega|}{2\pi}\) 叫做频率。

\(y=A\sin(\omega x+\varphi)\) 可以看做 \(y=A\sin(x+\varphi)\) 进行周期变换，把横坐标变为原来的 \(\frac{1}{\omega}\) 倍，纵坐标不变得到的。

posted @ 2022-01-20 20:51  lxgw  阅读(729)  评论(0)    收藏  举报