【LeetCode 240】算法：搜索二维矩阵 II

题目：编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。

每列的元素从上到下升序排列。

---

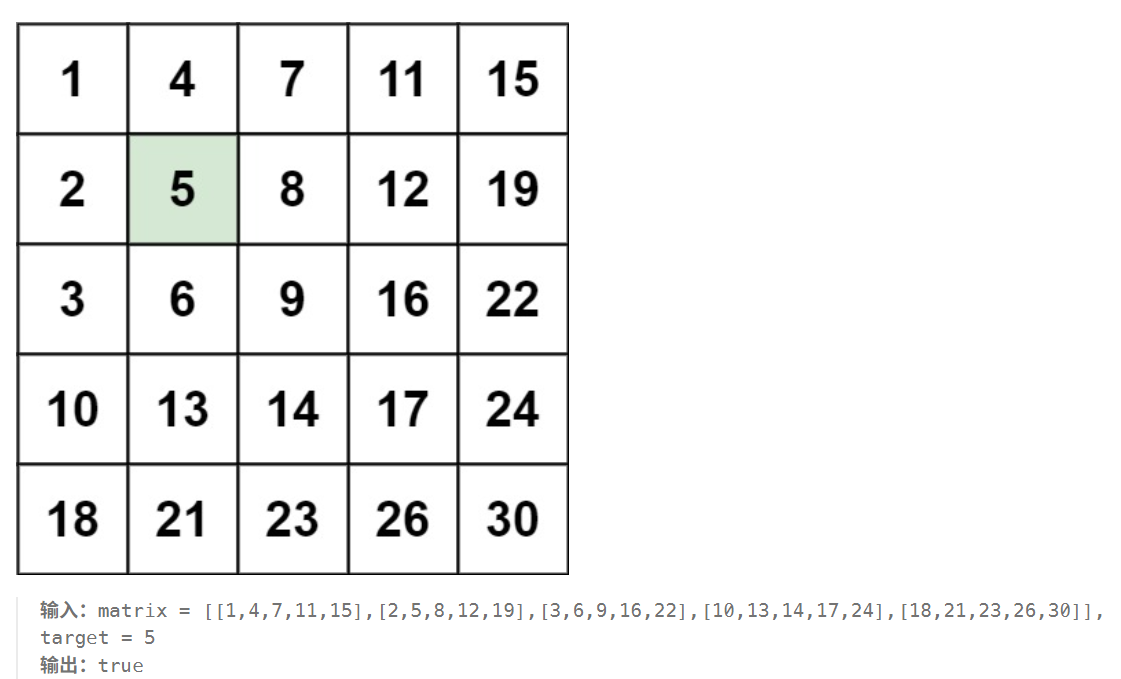
对于这个问题，可以利用矩阵的有序性来设计一个最高效的搜索算法。由于矩阵的每行和每列都是升序排列的，我们可以从矩阵的右上角开始搜索，根据目标值与当前元素的大小关系来决定搜索的方向。

算法思路：

1. 从右上角开始搜索：

• 如果目标值等于当前元素，返回 true。

• 如果目标值小于当前元素，向左移动（减小列索引）。

• 如果目标值大于当前元素，向下移动（增加行索引）。

2. 边界条件：

• 如果超出矩阵的边界（行或列），说明目标值不存在，返回 false。

算法分析：

• 时间复杂度：最多需要 m+n 次比较，其中 m 是行数，n 是列数。因此，时间复杂度为 O(m+n)。

• 空间复杂度：只使用了常数级的额外空间，空间复杂度为 O(1)。

不同方法的对比：

• 二分查找法：对矩阵的每一行分别进行二分查找。适用于每一行或每一列，但需要逐行或逐列进行，时间复杂度为 O(mlogn)。

• 分治法：将矩阵分成四个子矩阵，分别在每个子矩阵中查找目标值。由于矩阵的有序性是局部的（每行和每列有序），而不是全局的，分治法并不能显著减少搜索范围。虽然可以尝试，但效果并不理想，时间复杂度仍然接近 O(m+n)。

• 从右上角开始搜索：利用矩阵的有序性，时间复杂度为 O(m+n)，是最高效的方法。

我的 Java 代码：

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }

        // 从右上角开始搜索，逐步往内移
        int row = 0;                    // 初始行索引
        int col = matrix[0].length - 1; // 初始列索引

        while (row < matrix.length && col >= 0) {
            if (matrix[row][col] == target) {
                return true; // 1.找到目标值
            } else if (matrix[row][col] > target) {
                col--; // 2.大于目标值，向左移动
            } else {
                row++; // 3.小于目标值，向下移动
            }
        }

        return false; // 4.超出边界，未找到目标值
    }
}