【LeetCode 48】力扣算法：旋转图像

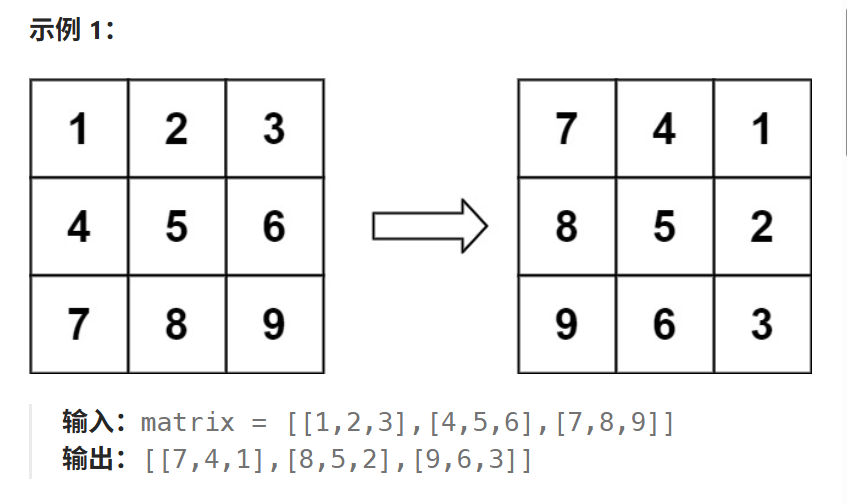
题目：给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

---

旋转思路：

1. 转置矩阵：先将矩阵转置，即将矩阵的行和列元素互换。

2. 反转每一行：转置后，对每一行元素进行反转，即互换行对称位置的元素。

具体步骤：

1. 转置矩阵：对于矩阵中的每个元素 matrix [i] [j]，将其与 matrix [j] [i] 交换，其中 i≤j（避免重复交换）。

2. 反转每一行：对于每一行，交换第 k 个元素和第 n−1−k 个元素，直到所有行都完成反转。

时间复杂度：

• 转置矩阵的时间复杂度为 O (n^2)

• 反转每一行的时间复杂度为 O (n^2)

• 总时间复杂度为 O (n^2)

空间复杂度：

• 由于是原地操作，空间复杂度为 O (1)

我的 Java 代码：

class Solution {
    public void rotate(int[][] matrix) {
        
        int n = matrix.length; // 获取矩阵行数

        // 第一步：转置矩阵
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) { // 只遍历上三角部分，避免重复交换
                // 交换 行列元素
                int t = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = t;
            }
        }

        // 第二步：根据中线，反转每一行
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n / 2; j++) { // 遍历到行的一半就停止
                // 交换 行对称位置的元素
                int t = matrix[i][j];
                matrix[i][j] = matrix[i][n - 1 - j];
                matrix[i][n - 1 - j] = t;
            }
        }
    }
}