【LeetCode 73】算法：矩阵置零 —— 进阶版：空间复杂度 O (m+n)

题目：给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

---

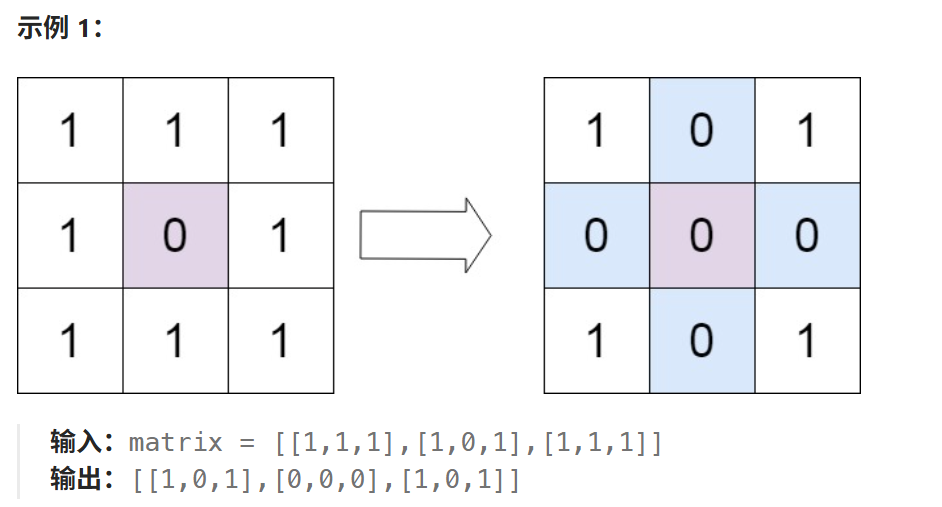
解决这个问题，需要使用原地算法，意味着将直接在输入矩阵上进行操作，所以不需要额外的存储空间。

算法步骤：

1. 标记需要置0的行和列：

  首先，创建两个布尔数组 row 和 col 来标记需要置0的行和列。

  然后，我们遍历矩阵，如果发现某个元素为0，就在对应的行和列标记数组中设置为 true。

2. 根据标记更新矩阵：

  我们再次遍历矩阵，如果某个元素所在的行或列被标记为需要置0，就将该元素置为0。

时间复杂度：O(m×n)，其中 m 是矩阵的行数，n 是矩阵的列数。我们需要遍历整个矩阵两次。

空间复杂度：O(m+n)，我们使用了两个额外的数组来存储行和列的标记信息。

这种方法的优点是它不需要额外的存储空间（除了几个变量），并且可以直接在原矩阵上进行操作。

我的 Java 代码：

public class Solution {
    public void setZeroes(int[][] matrix) {
        
        int rlength = matrix.length;     // 行大小
        int clength = matrix[0].length;  // 列大小
        
        if (matrix == null || rlength == 0 || clength == 0) {
            return;
        }

        // 布尔数组记录需要置0的行和列
        boolean[] row = new boolean[rlength];
        boolean[] col = new boolean[clength];

        // 标记需要置0的行和列
        for (int i = 0; i < rlength; i++) {
            for (int j = 0; j < clength; j++) {
                if (matrix[i][j] == 0) {
                    row[i] = true;
                    col[j] = true;
                }
            }
        }

        // 根据标记更新矩阵
        for (int i = 0; i < rlength; i++) {
            for (int j = 0; j < clength; j++) {
                if (row[i] || col[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}