RSA算法

本文转载自https://zhuanlan.zhihu.com/p/48249182

RSA算法原理

1. 数论基础

1.1 素数

    素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数.

1.2 模运算

    "mod"，与同余关系密切.

1.3 互质关系

     如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）.

1.4 欧拉函数

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）

   计算这个值的方法就叫做欧拉函数，以φ(n)表示。在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4.

（1）n=1，φ(1)=1     （1与任何数互质，包括本身）.

（2）如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系.

（3）如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则φ(p^k) = p^k-p^k-1.

（4）如果n可以分解成两个互质的整数之积   n = p1 × p2，则 φ(n) = φ(p1p2) = φ(p1)φ(p2)     即积的欧拉函数等于各个因子的欧拉函数之积.

（5）欧拉函数的通用计算公式：

1.5 欧拉定理

     如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：（a的φ(n)次方被n除的余数为1）

欧拉定理有一个特殊情况：（这就是著名的费马小定理）

假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

1.6 模反元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1.

如：3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。模反元素不只一个，如果b是a的模反元素，则 b+kn 都是a的模反元素.

欧拉定理可以用来证明模反元素必然存在：

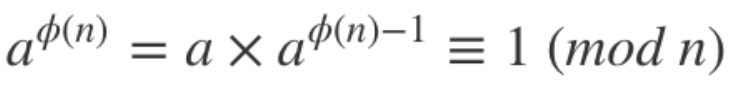
 可以看到，a的 φ(n)-1 次方，就是a的模反元素.

2. RSA算法

2.1 密钥生成步骤

p,q,n,φ(n),e,d

（1）随机选取两个不等质数p,q，n=p×q;

（2）计算n的欧拉函数φ(n) = (p-1)(q-1)；

（3）随机选择一个整数e，满足条件1<e<φ(n)，且e与φ(n)互质；

（4）计算e对φ(n)的模反元素d，即：ed ≡ 1(modφ(n))

（5）最后，n和e封装成公钥，n和d封装成私钥.

2.2 RSA算法的可靠性

公钥(n,e)，其他p，q，φ(n)，d 不公开. 如果 n 可以被因数分解，d 就可以算出，也就意味着私钥被破解。

对极大整数做因数分解的难度决定了RSA算法的可靠性。目前被破解的最长RSA密钥是768位。

2.3 RSA算法的加密和解密

设明文信息为 m( m<n )，密文为 c .

加密规则为：m^e ≡ c(mod n)  .

解密规则为：c^d ≡ m(mod n) .