关于二维电阻网络

关于二维无穷网络

从《 物理学难题集萃 》（ 上册 ） P 611 【 题 19 】 开始
对于一个二维无穷网络，如图

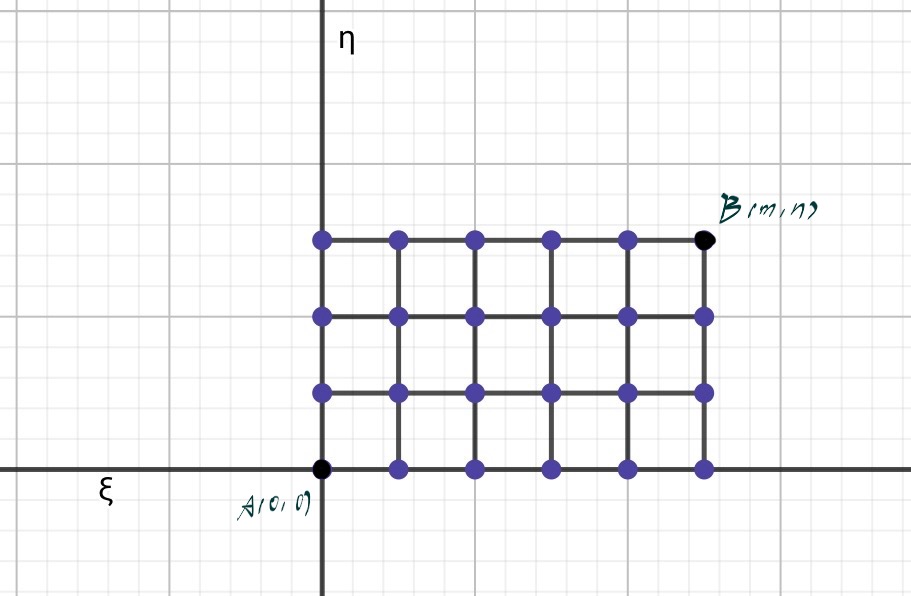
我只画出来了其中一部分

物理层面上的电流分析

建立一个 $ \xi \eta $ 坐标系，定义 $ I \ ( \ k \ , \ l \ ) $ 为流入点 $ ( \ k \ , \ l \ ) $ 的电流，有

\[I \ ( \ k \ , \ l \ ) = \begin{cases} I & k = l = 0 \\ - I & k = m , l = n \\ 0 & k , l \text{为其他值} \end{cases} \]

对于节点 $ ( \ k \ , \ l \ ) $ ，电势记为 $ V \ ( \ k \ , \ l \ ) $ ，有

\[V \ ( \ k \ , \ l \ ) = I \ ( \ k \ , \ l \ ) + \frac{ 1 }{ r } [ \ V \ ( \ k - 1 \ , \ l \ ) - V \ ( \ k \ , \ l \ ) \ ] + \frac{ 1 }{ r } [ \ V \ ( \ k + 1 \ , \ l \ ) - V \ ( \ k \ , \ l \ ) \ ] + \frac{ 1 }{ r } [ \ V \ ( \ k \ , \ l - 1 \ ) - V \ ( \ k \ , \ l \ ) \ ] + \frac{ 1 }{ r } [ \ V \ ( \ k \ , \ l + 1 \ ) - V \ ( \ k \ , \ l \ ) \ ] \]

引入算符 $ \mathscr{ L } V \ ( \ k \ , \ l \ ) $，有

\[\mathscr{ L } V \ ( \ k \ , \ l \ ) = \frac{ 1 }{ 4 } [ \ V \ ( \ k - 1 \ , \ l \ ) + \ V \ ( \ k + 1 \ , \ l \ ) + \ V \ ( \ k \ , \ l - 1 \ ) + \ V \ ( \ k \ , \ l + 1 \ ) ] \]

故而节点电流方程可以写成

\[\frac{ r }{ 4 } I \ ( \ k \ , \ l \ ) = V \ ( \ k \ , \ l \ ) - \mathscr{ L } V \ ( \ k \ , \ l \ ) \]

解这个 微 伪分方程
对应的 齐次方程

\[V \ ( \ k \ , \ l \ ) - \mathscr{ L } V \ ( \ k \ , \ l \ ) = 0 \]

其在物理上的理解，相应于 $ I \ ( \ k \ , \ l \ ) $ 一概为零的情况，则有

\[V _ 1 \ ( \ k \ , \ l \ ) = V _ 0 \]

乱入的 Fourier 级数

我们知道，对于任意的一个周期函数，可以展开成一个 $ Fourier $ 级数，即

\[F \mspace{ 2mu } ( \mspace{ 2mu } x \mspace{ 2mu } ) = \sum ^ \infty _ { n \mspace{ 2mu } = \mspace{ 2mu } - \infty } c _ n \mathrm{ e } ^ { i \frac{ n \pi x }{ l } } \]

那么，回到原方程，可将其视为

\[V \ ( \ k \ , \ l \ ) - \alpha \mathscr{ L } V \mspace{ 2mu } ( \ k \ , \ l \ ) = \frac{ 1 }{ 4 } r I \mspace{ 2mu } ( \ k \ ,\ l \ ) \]

$ 0 < \alpha < 1 $ 时在 $ \alpha \rightarrow 1 $ 时的极限解，
寻找函数 $ F \mspace{ 2mu } ( \mspace{ 2mu } x \mspace{ 2mu} , \mspace{ 2mu } y \mspace{ 2mu } ) $ 使得它能在区间 $ [ \mspace{ 2mu } - \pi , \pi \mspace{ 2mu } ; \mspace{ 2mu } - \pi , \pi \mspace{ 2mu } ] $ 展开成二维 $ Fourier $ 级数，且以 $ V \ ( \ k \ , \ l \ ) $ 为其 $ ( \ k \ , \ l \ ) $ 级 $ Fourier $ 系数，即有

\[F \mspace{ 2mu } ( \ k \ , \ l \ ) = \sum _ { k \ , \ l } V \mspace{ 2mu } ( \ k \ , \ l \ ) \ \mathrm{ e } ^ { i \mspace{ 2mu }( k x + l y ) } \]

代入节点电流方程，故

\[F \mspace{ 2mu } ( \mspace{ 2mu } x \mspace{ 2mu } , \mspace{ 2mu } y \mspace{ 2mu } ) = \sum _ { k \ , \ l } \left [ \ \alpha \mathscr{ L } V \ ( \ k \ , \ l \ ) + \frac{ 1 }{ 4 } r I \mspace{ 2mu } ( \ k \ , \ l \ ) \mspace{ 2mu } \right ] \mathrm{ e } ^ { i \mspace{ 2mu } ( k x + l y ) } \]

展开后

\[F \mspace{ 2mu } = \sum \left [ \frac{ 1 }{ 4 } r I \mspace{ 2mu } ( \ k \ , \ l \ ) \mathrm{ e } ^ { i \mspace{ 2mu } ( k x + l y ) } \right ] + \frac{ 1 }{ 4 } \alpha \sum \left [ \ V \mspace{ 2mu } ( \ k + 1 \ , \ l \ ) \ \mathrm{ e } ^ { i x } + V \mspace{ 2mu } ( \ k - 1 \ , \ l \ ) \ \mathrm{ e } ^ { - i x } + V \mspace{ 2mu } ( \ k \ , \ l + 1 \ ) \ \mathrm{ e } ^ { i y } + V \mspace{ 2mu } ( \ k \ , \ l - 1 \ ) \ \mathrm{ e } ^ { - i y }\right ] \mathrm{ e } ^ { i ( \ k x + \ l y ) } \]

考虑到求和是在无穷区间进行的，并且级数收敛于函数 $ F \mspace{ 2mu } ( \mspace{ 2mu } x \mspace{ 2mu } , \mspace{ 2mu } y \mspace{ 2mu } ) $ ，有原式

\[= \frac{ 1 }{ 4 } r \sum I \ ( \ k \ , \ l \ ) \mspace{ 2mu } \mathrm{ e } ^ { i \mspace{ 2mu } ( k x + l y ) } + \frac{ 1 }{ 4 } \alpha \sum \left [ \ V \ ( \ k \ , \ l \ ) ( \mspace{ 2mu } \mathrm{ e } ^ { i x } + \mathrm{ e } ^ { - i x } + \mathrm{ e } ^ { i y } + \mathrm{ e } ^ { - i y } \mspace{ 2mu } ) \mspace{ 2mu } \mathrm{ e } ^ { i \mspace{ 2mu } ( k x + l y ) } \right ] \]

\[= \frac{ 1 }{ 4 } r I \mspace{ 2mu } \left [ \mspace{ 2mu } 1 - \mspace{ 2mu }\mathrm{ e } ^ { i \mspace{ 2mu } ( m x + n y ) }\mspace{ 2mu } \right ] + \frac{ 1 }{ 4 } ( \mspace{ 2mu } \mathrm{ e } ^ { i x } + \mathrm{ e } ^ { - i x } + \mathrm{ e } ^ { i y } + \mathrm{ e } ^ { - i y } \mspace{ 2mu } ) \sum \ V \ ( \ k \ , \ l \ ) \ \mathrm{ e } ^ { i \mspace{ 2mu } ( k x + l y ) } \]

\[= \frac{ 1 }{ 4 } r I \mspace{ 2mu } [ \mspace{ 2mu } 1 - \mspace{ 2mu } \cos \mspace{ 2mu } ( m x + n y ) \ ] + \frac{ 1 }{ 2 } \alpha \mspace{ 2mu } ( \mspace{ 2mu } \cos x + \cos y \mspace{ 2mu } ) \mspace{ 2mu } F \mspace{ 2mu } ( \mspace{ 2mu } x \mspace{ 2mu } , \mspace{ 2mu } y \mspace{ 2mu } ) \]

\[\Rightarrow F \, ( \mspace{ 2mu } x \mspace{ 2mu } , \mspace{ 2mu } y \mspace{ 2mu } ) = \frac{ r I \mspace{ 2mu } [ \mspace{ 2mu } 1 - \cos ( \mspace{ 2mu } m x + n y \mspace{ 2mu } ) \mspace{ 2mu } ] }{ 2 \mspace{ 2mu } [ \mspace{ 2mu } 2 - \alpha \mspace{ 2mu } ( \, \cos x + \cos y \, ) \, ] } \]

对于 $ 0 < \alpha < 1 $ ，有

\[V \, ( \, 0 \, , \, 0 \, ) _ { \alpha } = \frac{ 1 }{ 4 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } F \, ( \, x \, , \, y \, ) \,\mathrm{ d } x \, \mathrm{ d } y \]

\[V \, ( \, m \, , \, n \, ) _ { \alpha } = \frac{ 1 }{ 4 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } F \, ( \, x \, , \, y \, ) \, \mathrm{ e } ^ { - i \, ( m x + n y ) } \,\mathrm{ d } x \, \mathrm{ d } y \]

在 $ \alpha \rightarrow 1 $ 时

\[\Rightarrow \left \{ \begin{array} { r1 } V \, ( \, 0 \, , \, 0 \, ) _ 2 & = & \frac{ I r }{ 8 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } \frac{ 1 \, - \ \cos \ ( \, m x + n y \, ) }{ 2 \, - \ ( \mspace{ 1mu } \cos x + \cos y \mspace{ 2mu } ) } \mathrm{ d } x \mathrm{ d } y \\ V \, ( \, m \, , \, n \, ) _ 2 & = & - \frac{ I r }{ 8 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } \frac{ 1 \, - \ \cos \ ( \, m x + n y \, ) }{ 2 \, - \ ( \mspace{ 1mu } \cos x + \cos y \mspace{ 2mu } ) } \mathrm{ d } x \mathrm{ d } y \end{array} \right . \]

\[\Rightarrow \left \{ \begin{array} { r1 } V \, ( \, 0 \, , \, 0 \, ) & = & V _ 0 + \frac{ I r }{ 8 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } \frac{ 1 \, - \ \cos \ ( \, m x + n y \, ) }{ 2 \, - \ ( \mspace{ 1mu } \cos x + \cos y \mspace{ 2mu } ) } \mathrm{ d } x \mathrm{ d } y \\ V \, ( \, m \, , \, n \, ) & = & V _ 0 - \frac{ I r }{ 8 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } \frac{ 1 \, - \ \cos \ ( \, m x + n y \, ) }{ 2 \, - \ ( \mspace{ 1mu } \cos x + \cos y \mspace{ 2mu } ) } \mathrm{ d } x \mathrm{ d } y \end{array} \right. \]

\[R _ { m n } = \frac{ \left \vert V \, ( \, m \, , \, n \, ) - V \, ( \, 0 \, , \, 0 \, ) \right \vert }{ I } \]

\[= \frac{ r }{ 4 \pi ^ 2 } \int ^ { \pi } _ { - \pi } \int ^ { \pi } _ { - \pi } \frac{ 1 \, - \, \cos \ ( \, m x + n y \, ) }{ 2 \, - \ ( \mspace{ 1mu } \cos x + \cos y \mspace{ 2mu } ) } \,\mathrm{ d } x \mathrm{ d } y \]

很好原题的解答就到此为止啦，我们也到此为止吧
来看看这玩意的积分解
好吧这是个不太可积的函数，但是凡事都有但是。
倘若这个积分真的不可求，那么这个结论又有什么用？好吧可以求得一部分的数值解，但这是不美的（数值解哪里美了老弟）。
我可以换个方式 —— 椭圆积分
这很明显，因为 $ x = y = - \pi $ 时很明显不收敛

乱入的 Green 函数

好吧其实是我肤浅了，在 超理论坛的一个帖子上 翻看，发现这玩意是一个 $ Lattice \ Green \ Function $ （ 晶格的格林函数 ），关于这个函数的导出我们暂且可以不管。
定义一个 $ Lattice \ Green $ 函数

\[G ^ \square _ { p , q } = \frac{ 1 }{ 4 \pi ^ 2 } \int ^ { 2 \pi } _ 0 \int ^ { 2 \pi } _ 0 \frac{ e ^ { i ( p \theta _ 1 + q \theta _ 2 ) } \mathrm{ d } \theta _ 1 \mathrm{ d } \theta _ 2 }{ 4 - 2 \cos \theta _ 1 - 2 \cos \theta _ 2 } \]

写它的预积函数

\[H _ { r , s } ( t ) = \frac{ 1 }{ ( 2 \pi i ) ^ 2 } \oint _ { \vert x \vert = 1 } \oint _ { \vert y \vert = 1 } \frac{ \mathrm{ d } x }{ x } \frac{ \mathrm{ d } y }{ y } \frac{ x ^ r y ^ s }{ 4 t - ( x + \frac{ 1 }{ x } )( y + \frac{ 1 }{ y } ) } \]

其中 $ t $ 是一个复参数，而

\[x = e ^ { i \frac{ \theta _ 1 + \theta _ 2 }{ 2 } } , y = e ^ { i \frac{ \theta _ 1 - \theta _ 2 }{ 2 } } \]

故而不难求得两者的关系为

\[G ^ \square _ { p , q } = \frac{ 1 }{ 8 \pi ^ 2 } H _ { p + q , p - q } ( 1 ) \]

由于中间的过程超越了我的理论水平，在此处先跳跃掉这一部分，直接写结果

\[H _ { r , s } ( t ) = \left ( \frac{ 1 }{ 4 t } \right ) ^ { 1 + r } \sum ^ \infty _ { n = 0 } \frac{ \Gamma ( 1 + r + 2 n ) ^ 2 }{ \Gamma ( 1 + r + n ) \Gamma ( 1 + \frac{ r + s }{ 2 } + n ) \Gamma ( 1 + \frac{ r - s }{ 2 } + n ) } \left ( \frac{ 1 }{ 16 t ^ 2 } \right ) ^ n \frac{ 1 }{ n ! } \]

而我们所要求的

\[\begin{align} R _ { m n } & = r \cdot 2 \mspace{ 2mu } ( G _ { 0 , 0 } - G _ { m , n } ) \\ & = \frac{ r }{ 4 \pi ^ 2 } [ \mspace{ 2mu } H _ { 0 , 0 } ( 1 ) - H _ { m + n , m - n } ( 1 ) \mspace{ 2mu } ] \\ & = \frac{ r }{ 4 \pi ^ 2 } \left [ \frac{ 1 }{ 4 } \sum ^ \infty _ { k = 0 } \frac{ \Gamma ( 1 + 2 k ) ^ 2 }{ \Gamma ( 1 + k ) ^ 3 } - \frac{ 1 }{ 4 ^ { m + n } } \sum ^ \infty _ { k = 0 } \frac{ \Gamma ( 1 + m + n + 2 k ) ^ 2 }{ \Gamma ( 1 + m + n + k ) \Gamma ( 1 + m + k ) \Gamma ( 1 + n + k ) } \frac{ 1 }{ 16 ^ k } \frac{ 1 }{ k ! } \right ] \end{align} \]

即为最终的结果

参考文献

arXiv:1409.7806v1 Koushik Ray