磁透鏡

---

電子透鏡

基本模型

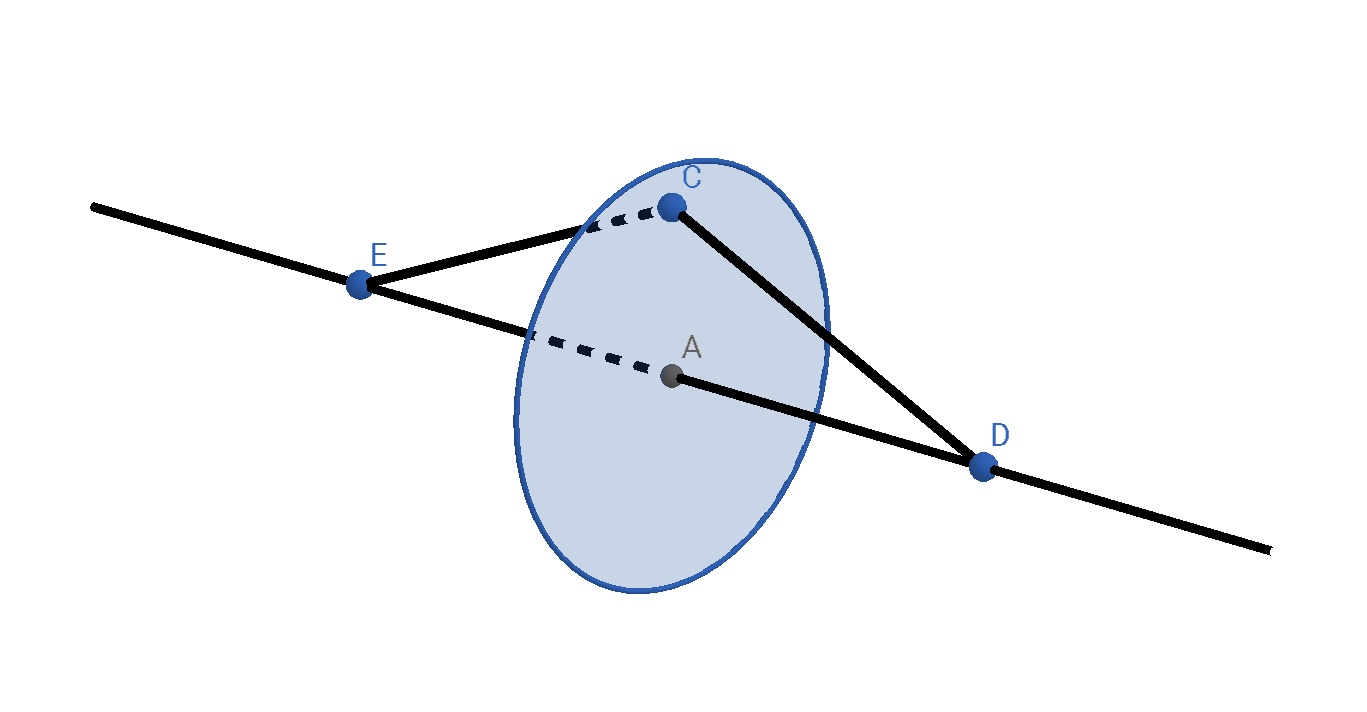
基本模型為一個導線圓環，半徑為 \(R\) ，有沿著順時針或是逆時針分布的電流，一般界定圓環軸線上的磁場方向與電子軸向速度的方向相同， 因為圖中我沒有標注電子的速度方向故而也沒有標注電流方向。
一般考慮以圓心為原點建立 柱坐標系 ，$ z $ 軸方向垂直於圓面。而後用 $$ ( r , \theta , z) $$ 來表示電子的實時位置。
為了求解該問題，首先便要得出磁場的表達式。

磁場求解

考慮到計算的簡便以及實際情況，要求電子在 $ r << R $ 的範圍內運動。
從大腦的記憶中不斷搜取，發現：

\[\displaystyle B _ z = \frac { \mu_0 I R }{ 2( R ^ 2 + z ^ 2)^{ \frac{ 3 }{ 2 }}} \]

而後如下圖取一柱狀 $ Gauss $ 面

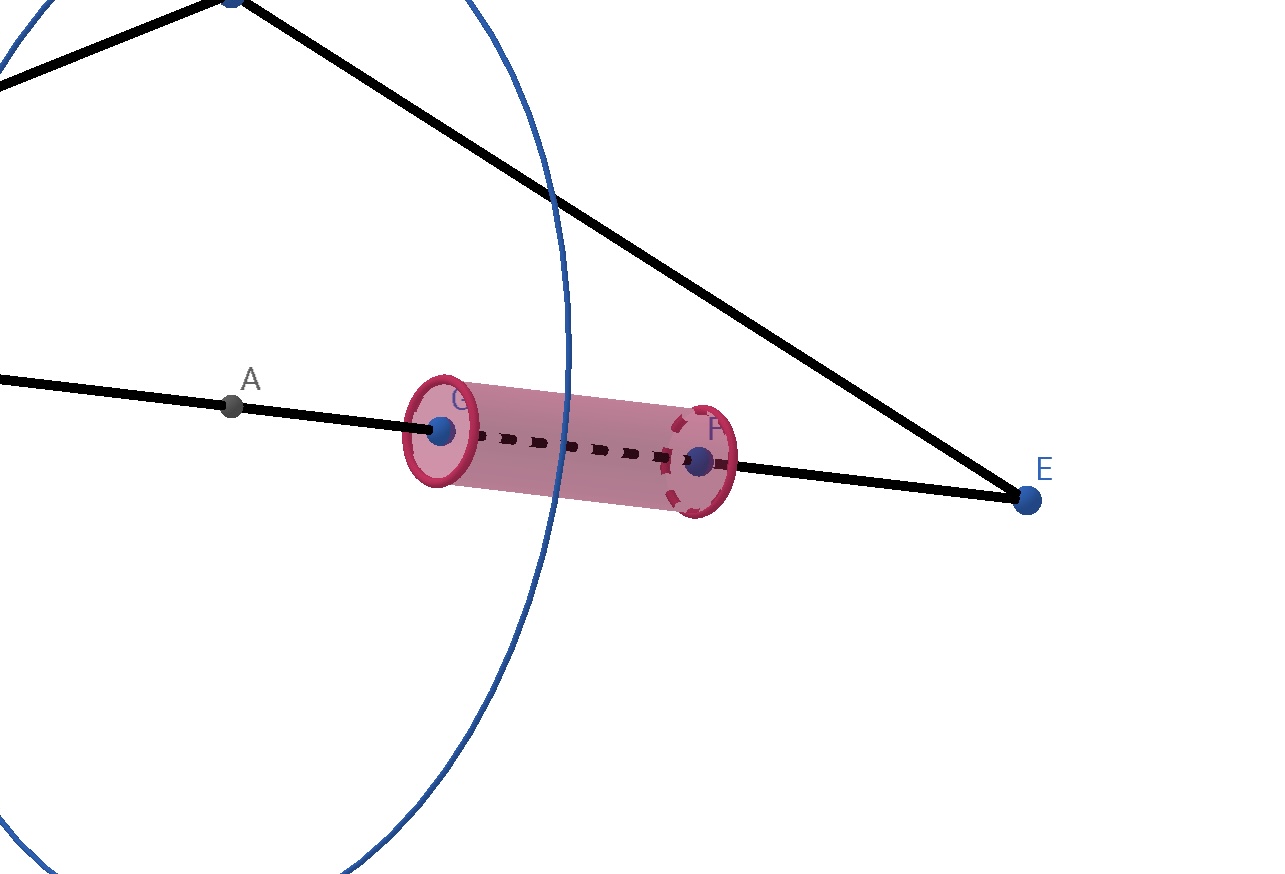
會發現，靜磁場的 $ Gauss $ 定理

\[\displaystyle \iint \overrightarrow{ B } \cdot d \vec{ S } = 0 \]

嗯，這是個閉合曲面。
得到

\[\displaystyle B_z \cdot \pi r^2 = B_{ z + \Delta z } \cdot \pi r^2 + B_r \cdot 2 \pi r \cdot \Delta z \]

故而有

\[\displaystyle B_r = - \frac{ r }{2} \cdot \frac { dB_z }{ dz } = \frac{ 3 \mu_0 I R ^ 2 r z }{ 4 ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } \]

整體表示一下磁場就是

\[\displaystyle \vec{ B } = \frac{ \mu_0 I R ^ 2 }{ 2 ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } }} \vec{ k } + \frac{ 3 \mu_0 I R ^ 2 r z }{ 4 ( z ^ 2 + R ^ 2 ) ^ { \frac { 5 }{ 2 } } } \vec{ n } \]

磁場表示完後，下一步便是分析受力。

受力分析

直接運用 $ Lorentz $ 力的公式，有

\[\vec{ F } = q \vec{ v } \times \vec{ B } \]

鑒於 Metion 目前無法使用 $ matrix $ 和 $ align $ 我只好直接給出矢量計算結果而繞開行列式計算過程。

\[\displaystyle \vec{ F } = q \cdot ( \dot{ \mathstrut r } \vec{ n } + r \mspace{ 2mu } \dot{ \mathstrut \theta } \vec{ \tau } + \dot{ \mathstrut z } \vec{ k } ) \times \left ( \frac{ 3 \mu_0 I R ^ 2 r z }{ 4 ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } \vec{ n } + \frac{ \mu_0 I R }{ 2 ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \vec{ k } \right ) \]

\[\displaystyle \mspace{ 13mu } = q \cdot \left [ B_z \mspace{ 2mu } \dot{ \theta } \mspace{ 2mu } r \mspace{ 2mu } \vec{ n } \ + ( B_r \dot{ \mathstrut z } \mspace{ 2mu } - B_z \dot{ \mathstrut r } ) \vec{ \tau } - B_r \dot{ \mathstrut \theta } \mspace{ 2mu } r \vec{ k } \ \right ] \]

這個時候就應該寫分量式了

\[\displaystyle F_r = m (\ddot{ \mathstrut r} -r \mspace{ 2mu } \dot{{ \mathstrut \theta } ^ 2 } ) = q B _ z \dot{ \mathstrut \theta } r = \frac{ \mu_0 I q \mspace{ 2mu } R \dot{ \mathstrut \theta } \mspace{ 2mu } r }{ 2 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \]

\[\displaystyle F_{ \theta } = m ( 2 \dot{ \mathstrut r } \dot{ \mathstrut \theta } \ + r \ddot{ \mathstrut \theta } \mspace{ 2mu } ) = q \mspace{ 2mu } ( B_r \dot{ \mathstrut z } \ + B_z \dot{ \mathstrut z } ) = q \left [ \frac{ 3 \mu_0 I R ^ 2 }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } r z \dot{ \mathstrut z } + \frac{ \mu_0 I R }{ 2 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \dot{ \mathstrut r } \mspace{ 2mu } \right ] \]

\[\displaystyle F_z = m \ddot{ \mathstrut z } = - q B_r \dot{ \mathstrut \theta } \mspace{ 2mu } r = - \frac{ 3 \mu_0 I q R ^ 2 \dot{ \mathstrut \theta } r ^ 2 z }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } \]

這可怎麼辦哪 這我不好算
不管怎麼說，磁場和受力已經搞完了，下面就 是飛行時間

角動量分析

眾所週知 $ L = m r ^ 2 \dot{ \mathstrut \theta } $
但是眾所不知 $$ \displaystyle \frac{ \mathrm d L }{ \mathrm d t }= m r \mspace{ 2mu } ( \mspace{ 2mu } 2 \dot{ \mathstrut r } \dot{ \mathstrut \theta } + r \mspace{ 2mu } \ddot{ \mathstrut \theta } \mspace{ 2mu } ) = r \mspace{ 2mu } \cdot F_{ \theta } $$

\[\displaystyle \qquad \qquad \qquad \quad \; \; \, \, = q \ \left [ \frac{ 3 \mu_0 I R ^ 2 }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } r z \dot{ \mathstrut z } - \frac{ \mu_0 I R }{ 2 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \dot{ \mathstrut r } \mspace{ 2mu } \right ] \]

好吧這是我瞎編的
本題的一大特徵便是極其大膽的 小量近似 ，採取了以下四個假設：
$ \S $ 假定 $ r $ 的變化很小，故可將其視為一個常量
$ \S $ 由於 $ r $ 方向的速度相較於 $ z $ 方向的速度很小，故將去略去，即假定 $$ \dot{ \mathstrut r } = 0 $$
$ \S $ 由於將徑向的速度忽略，可以一併假設 $ z $ 方向的速度為常量，即 $$ \dot{ \mathstrut z } = v _ 0 $$
$ \S $ 綜合以上假設，不妨假設電子在通過透鏡時動量為脈衝變化，即在之前電子以近似直線的軌跡運動
根據這幾大假設，不難發現

\[\frac{ \mathrm d L }{ \mathrm d t } = \frac{ 3 \mu_0 I q R ^ 2 r z }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } \dot{ \mathstrut z } \cdot r \]

積分呢，就有

\[\displaystyle L = \int _ 0 ^ t \frac{ 3 \mu _ 0 I q R ^ 2 r ^ 2 z }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } \mspace{ 2mu } \dot{ \mathstrut z } \mspace{ 2mu } \mathrm d t = \int _ 0 ^ z \frac{ 3 \mu _ 0 I q R ^ 2 r ^ 2 z }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 5 }{ 2 } } } \mathrm dz = \frac{ \mu _ 0 I q R ^ 2 r }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \]

\[\displaystyle \Longleftrightarrow m r ^ 2 \dot{ \mathstrut \theta } = \frac{ \mu _ 0 I q R ^ 2 r ^ 2 }{ 4 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \]

\[\displaystyle \Longleftrightarrow \frac{ \mathrm d \theta }{ \mathrm d t } = \frac{ \mu _ 0 I q R ^ 2 }{ 4 m \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \]

实际上这里的计算存在一些近似的失当，如果不做这么多的近似的话，可以发现

\[\frac{ \mathrm{ d } L }{ \mathrm{ d } t } = q \mspace{ 2mu } ( \dot{ z } B _ r - \dot{ r } B _ z ) = \frac{ q }{ 2 } \frac { \mathrm{ d } }{ \mathrm{ d } t } ( r ^ 2 B _ z ) \]

同样可以（或者说应该这样）就能得到一样的结果。

動量的脈衝變化

由 $ Newton $ 第二定律

\[\displaystyle \frac{ \mathrm d p _ r }{ \mathrm d t } = m \mspace{ 2mu } \ddot{ \mathstrut r } = q B _ z \dot{ \mathstrut \theta } r + m \dot{ \mathstrut \theta ^ 2 } r = \frac{ \mu_0 I q \mspace{ 2mu } R ^ 2 \dot{ \mathstrut \theta } \mspace{ 2mu } r }{ 2 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } + m \cdot \left [ \frac{ \mu _ 0 I q R ^ 2 }{ 4 m \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \right ] ^ 2 \cdot r \]

\[\displaystyle \mspace{ 33mu } = \frac{ \mu _ 0 I q R ^ 2 r }{ 2 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } \cdot \frac{ \mu _ 0 I q R ^ 2 }{ 4 m \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ { \frac{ 3 }{ 2 } } } + m \cdot \frac{ \mu _ 0 ^ 2 I ^ 2 q ^ 2 R ^ 4 }{ 16 m ^ 2 \mspace{ 2mu } ( z ^ 2 + R ^ 2 ) ^ 3 } \cdot r \]

\[\displaystyle \mspace{ 33mu } = - \frac{ \mu_0 ^ 2 I ^ 2 q ^ 2 R ^ 4 r }{ 16 m ( z ^ 2 + R ^ 2 ) ^ 3 } \]

有 $$ \mathrm d z = v _ 0 \mathrm d t $$

\[\displaystyle \mathrm d p _ r = - \frac{ \mu_0 ^ 2 I ^ 2 q ^ 2 R ^ 4 r }{ 16 m v _ 0 ( z ^ 2 + R ^ 2 ) ^ 3 } \mathrm d z \]

\[\displaystyle \Delta p _ r = - \frac{ \mu _ 0 ^ 2 I ^ 2 q ^ 2 R ^ 4 r }{ 16 m v _ 0 } \int _ { z _ 1 } ^ { z _ 2 } \frac{ \mathrm d z }{ ( z ^ 2 + R ^ 2 ) ^ 3 } \]

\[\displaystyle \mspace{ 30mu } = - \frac{ \mu _ 0 ^ 2 I ^ 2 q ^ 2 R ^ 4 r }{ 16 m v _ 0 } \cdot \left. \left [ \frac{ 3 \mathrm arctan ( \frac{ z }{ R } ) }{ 8 R ^ 5 } + \frac{ 3 x ^ 3 + 5 R ^ 2 x }{ 8 R ^ 4 ( x ^ 4 + 2 R ^ 2 x ^ 2 + R ^ 4 ) } \right ] \right \vert _ { z _ 1 } ^ { z _ 2 } \]

代 $ z _ 1 = - \infty , z _ 2 = \infty $ 入式，有

\[\displaystyle \Delta p _ r = - \frac{ \mu _ 0 ^ 2 I ^ 2 q ^ 2 R ^ 4 r }{ 16 m v _ 0 } \cdot \frac{ 3 \pi }{ 8 R ^ 5 } = - \frac{ 3 \pi \mu _ 0 ^ 2 I ^ 2 q ^ 2 r }{ 128 m v _ 0 R } \]

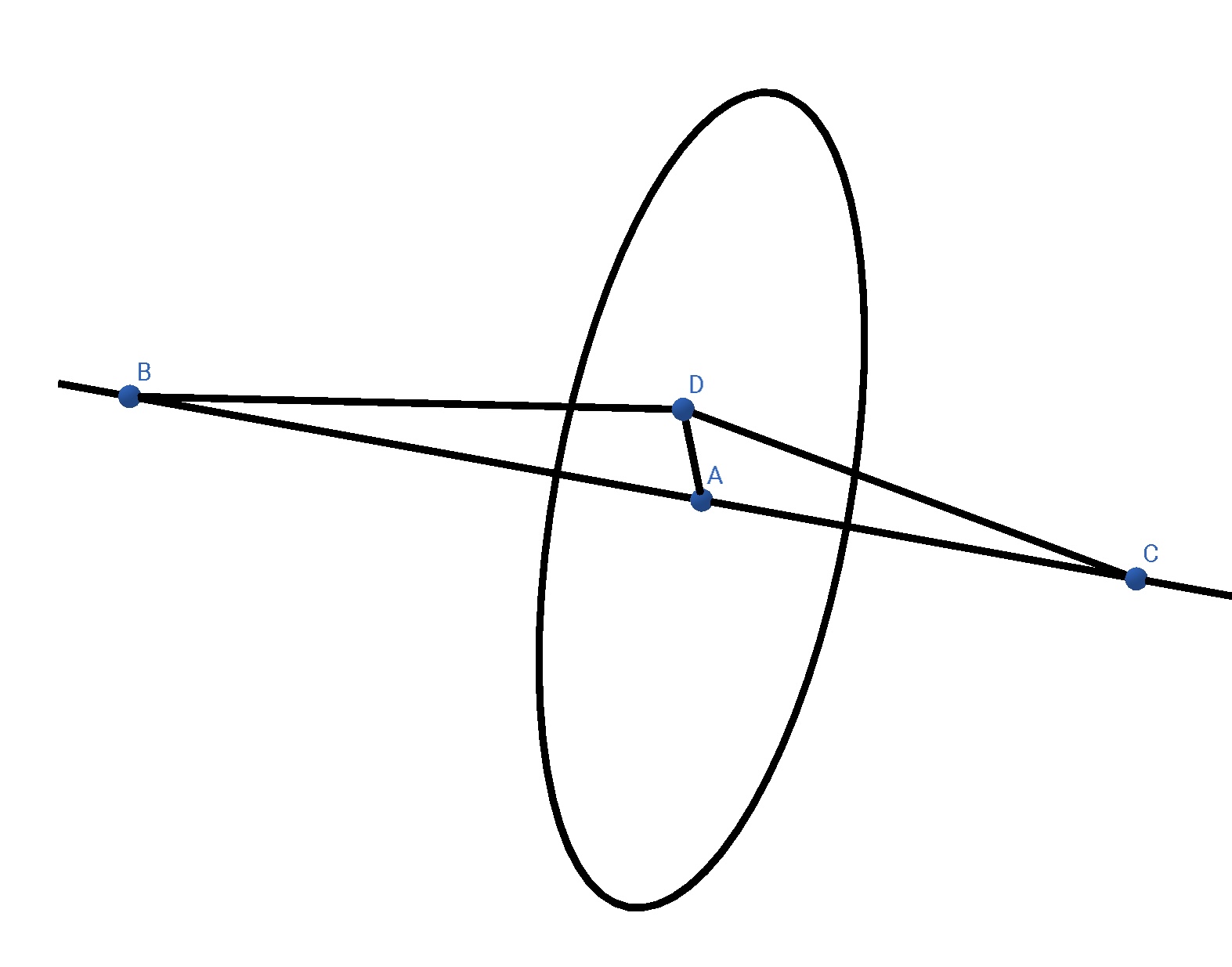
而後呢，設粒子出發時為 $ L _ 0 $ ，入射時為 $ L $ ，有

\[\displaystyle \frac{ p _ { 初 } }{ m v _ 0 } = \frac{ r }{ L _ 0 } , \ \frac{ - p _ { 末 } }{ m v _ 0 } = \frac{ r }{ L } , \ p _ { 末 } - p _ { 初 } = \Delta p _ r \]

\[\displaystyle \Rightarrow \frac{ 1 }{ L _ 0 } + \frac{ 1 }{ L } = \frac{ 3 \pi \mu _ 0 ^ 2 I ^ 2 q ^ 2 }{ 128 m ^ 2 v _ 0 ^ 2 R } \]

故而焦距為

\[\displaystyle f = \frac{ 128 m ^ 2 v _ 0 ^ 2 R }{ 3 \pi \mu _ 0 ^ 2 I ^ 2 q ^ 2 } \]