学习笔记：EMD方法

经验模态分解（Empirical Mode Decomposition, EMD） 

优点：能够对非线性、非平稳过程的数据进行线性化和平稳化处理，且经分解后的函数彼此正交，理论上互不相关，从而尽可能多的保留原始数据基本特征。

计算步骤：通过计算原序列 Y(t) 的上下包络线的“瞬时平衡位置”，提取内在模函数（IMF）。原序列减去该内在模函数后得到的序列作为新的原序列重复计算，如此依次提取出N个内在模函数，直至剩余值序列成为单调序列 r(t)，无法提取出内在模函数为止^[1]。

　　Y(t) = ∑ IMF + r(t)

 经EMD分解后得到n个频率由高到低的本征模函数IMF和一个残差项。

 由于每一个 IMF 分量是代表一组特征尺度（频率）的数据序列，因此 EMD 分解实际上就把原始数据序列分解为各种不同特征波动的叠加，每一个 IMF 分量既可以是线性的也可以是非线性的，且每个 IMF 分量都有实际的物理背景相对应^[4]。

 

内在模函数的特点：

　　其中 1）极值点的数目和跨零点的数目相等或至多只差一个，并且 2）各个瞬时平均值 m(t)都等于零（关于时间轴对称）,则它就是内在模函数。

　　在实际应用中，有时难以满足条件2，采用限制标准差的值作为替换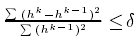：，delta 通常取 0.2 - 0.3 之间

 

提取内在模函数步骤：

　　1）找出原始序列 Y(t) 的局部极大值和局部极小值（例如，局部极大值定义为时间序列中的某个时刻的值，其前一时刻的值不比它大，后一时刻的值也不比它大）

　　2）使用三阶样条函数插入法进行插值，得到上下包络线 Ymax(t)，Ymin(t)

　　3）对上下包络线取平均，得到 m(t) = [Ymax(t)-Ymin(t)]/2，m(t) 代表信号 Y(t) 的低频数据

　　4）用原序列 Y(t) 减去瞬时平均值 m(t), 得到类距平值序列 h(t):h(t)= Y(t)-m(t)

　　5）检验 h(t) 是否为 IMF，若不是，将 h(t) 作为原序列，重复上述步骤，直至找到内在模函数为止

 

应用：　　

　　股票指数是非线性、非平稳的时间序列，我国股市数据具有时间序列短、随机因素多、价格波动变化剧烈等特点。

　　a. 使用EMD方法对金融价格序列（股指日收盘价）进行分解，剔除高频低相关IMF序列，选择其余IMF项和趋势项，作为特征进入BP网络训练，与小波神经网络预测结果对比，得出EDA神经网络更有效的结论^[2]。阅读中发现文章的方法或许用到了未来数据（使用当日分解函数预测当日收盘价）。

　　b. 使用EMD方法对金融价格序列（50综指日收盘数据）进行分解得到多个内在模函数和一个残差项，通过再重构将多个内在模函数分为三个再重构序列，分别代表股票的短期、中期和长期波动，并计算三个再重构序列与原序列的相关性。分别研究其对应的经济学背景和作用因素，分析其波动机制。结论：1）EMD分解具有有效性。2）重组后属于不同周期序列的各项 IMF 与残差项依旧带有明显的统计性质。3）分解结果中不同周期的波动序列带有不同的经济意义^[3]。

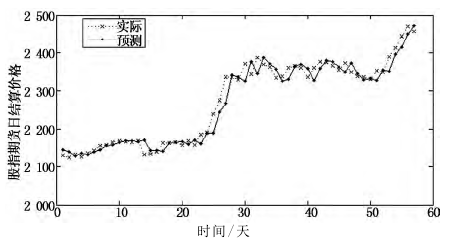
　　c. 使用EMD方法结合RBF（径向基函数）神经网络，搭建混合模型，对沪深300股指期货（2012-2014）日结算价数据进行训练和预测。就误差检测而言，结果优于传统GARCH、ARIMA模型。其中，在进行EMD运算之前，对原数据端点用多项式拟合算法做了处理，防止原序列极值端点出现发散现象并“污染”整个结果^[5]。

模型： 

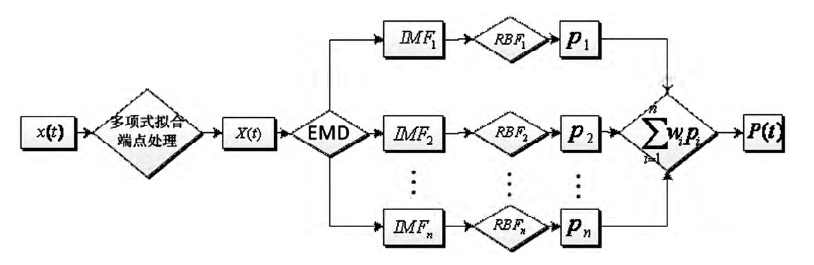
预测：走势的滞后性

 

 

参考文献：

• [1] 刘海飞,李心丹.  基于EMD方法的股票价格预测与实证研究[J]. 统计与决策. 2010(23)
• [2] 陈园园,刘俊,傅强.  基于EMD的神经网络股价预测方法[J]. 新疆大学学报(哲学·人文社会科学版). 2014(04)
• [3] 李正辉,梁永臻.  基于EMD分解的上证综合指数波动机制研究[J]. 广州大学学报(自然科学版). 2017(04)
• [4] 丁志宏,谢国权.  金融时间序列多分辨率实证研究的EMD方法[J]. 经济研究导刊. 2009(06)
• [5] 史文静,高岩.  EMD结合RBF神经网络新混合模型及股指期货价格预测[J]. 经济数学. 2015(01)