Set_ML

参考资料：斯坦福（http://cs231n.github.io/linear-classify/；http://cs231n.stanford.edu/slides/2017/）

　　　　　Mastering Machine Learning With scikit-learn

 

 

• 假设函数（Hypothesis Function）模型的知识表达：

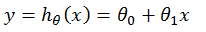
　　然后利用已知的数据对其中的参数进行求解，再将该函数用于新数据的预测，其中参数的求解过程称为“训练（Training） or 学习（Learning）”

• 待优化参数 θ₀，θ₁

• 损失函数(loss function)，或叫代价函数(cost function)

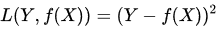
　　损失函数越小，就代表模型拟合的越好。

• 损失函数最小目标转换为经验风险最小化

　　由于我们输入输出的 遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集， 关于训练集的平均损失称作经验风险(empirical risk)，即 ，所以我们的目标就是最小化 ，称为经验风险最小化。

• 结构风险

　　为了平衡经验风险最小化目标与模型的复杂性（模型对数据的记性）引入结构风险，常用方法L1和L2范数。

• 目标函数

最终的优化函数是： ，即最优化经验风险和结构风险，而这个函数就被称为目标函数。

 

线性可分

 

• 线性回归与分类

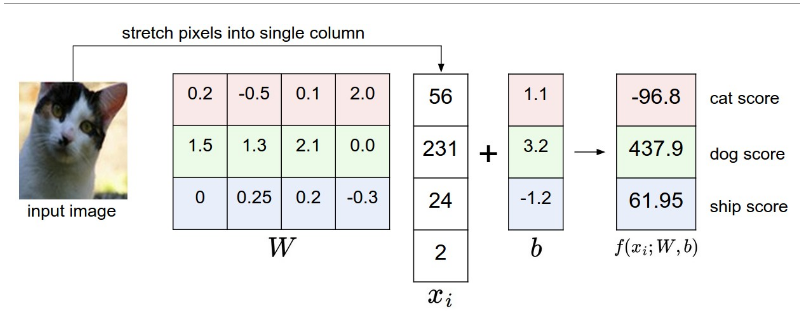
　　变换后：

 

 

　　线性回归

 

LinearRegression 回归

 

• 模型—线性最小二乘法（linear least squares）
• 函数表示—f(xi,W,b)=Wxi+b
• 损失函数—残差平方和（residual sum of squares）损失函数

 　　多元

　　多项式回归

 

 

 

　　线性分类

• 二分类

Logistic 分类器

 

• 模型—Bernoulli（伯努利） 分布
• 函数表示—logistic函数（sigmoid函数）

　　

• 多类

SVM

• 损失函数—折叶损失（hinge loss）

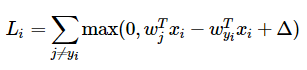
softmax

• 损失函数 —交叉熵损失（cross-entropy loss）

SVM vs. Softmax

 线性不可分

SVM

ANN