AT_codefestival_2016_final_g题解

一种可能理解起来比较自然的做法。

题意

一张有 $N$ 个点的图，有 $Q$ 次建边。每次给定三个数 $(A_i,B_i,C_i)$ 表示在 $A_i$和$B_i$ 之间建一条权值为$C_i$的无向边。之后在 $(A_i+1,B_i,C_i+1),(A_i+1,B_i+1,C_i+2),(A_i+2,B_i+1,C_i+3)...$ 同样建边。即每次建边 $(A_i+k,B_i+k,C_i+2k),(A_i+k+1,B_i+k,C_i+2k+1)$ 其中 $0\le k \le \infty$。求这个图的最小生成树

$2\le N \le 200000$ $1 \le Q \le 200000$

题目分析

最小生成树，输入又和边密不可分，很容易想到 Kruscal。 但是问题是，无限条边，直接跑肯定不现实，肯定需要寻找更优秀的方法。

性质1：总边数

我们可以尝试模拟一下一条边的情况，这里以 $n=4,A=0,B=2,C=1$ 为例

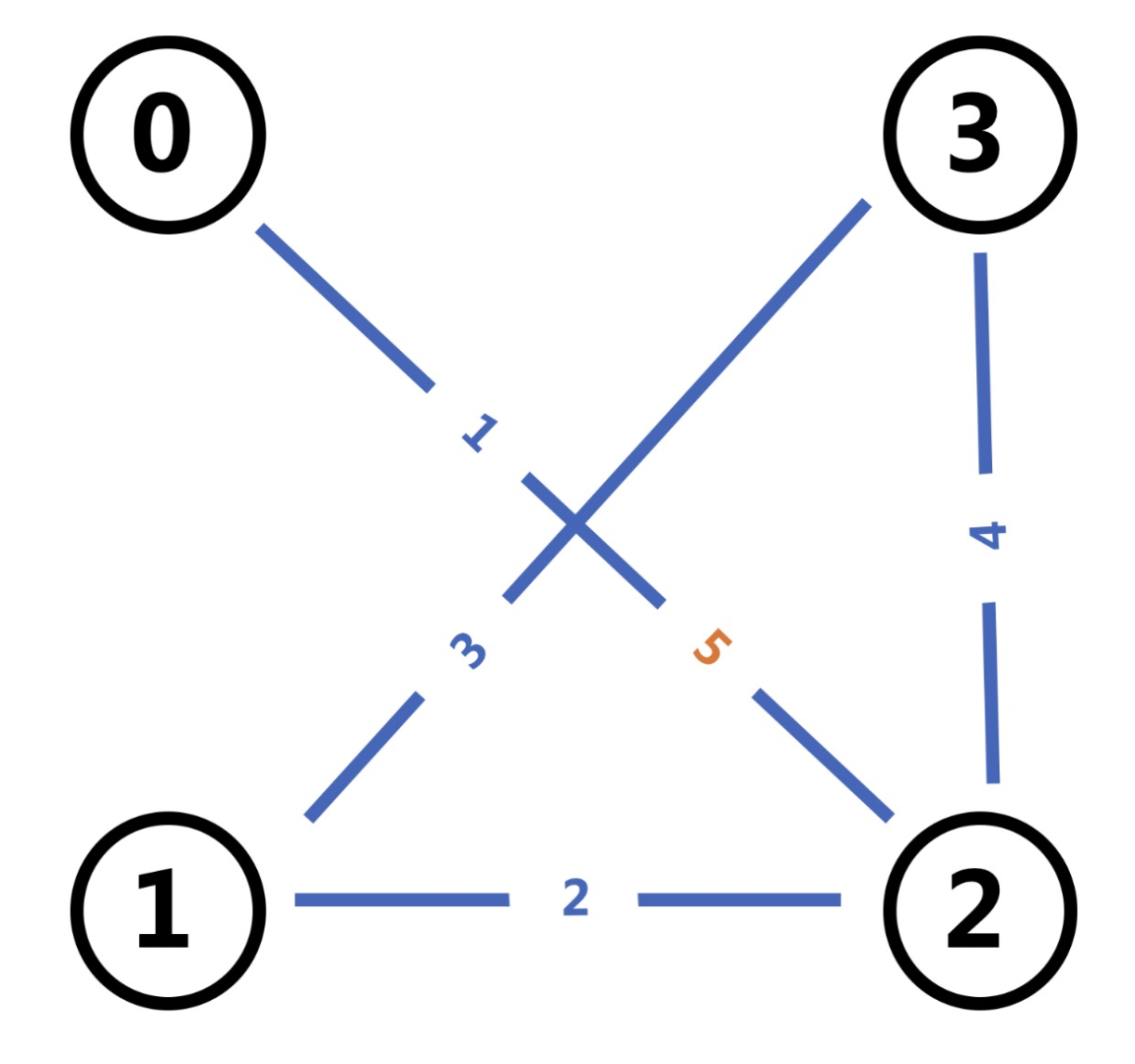
会发现这时候第五条边和第一条边是重叠的，那么，第六条边和第二条边也会是重叠的。

证明也非常简单，因为是在模 $n$ 意义下的，有 $A+n\equiv A \mod n$ 所以至多到第 $2n$ 条边，就会和之前的边重合了。

也就是说，并不是无限条边，每次建边最多只会建 $2n$ 条。

这里还会发现一个小性质，就是一条边通过操作，一定能够把图上所有的点都连通，因为每次+1，所以可以保证每个点都覆盖到。

这个时候我们就有一个暴力的思路，就是把这些边建出来，然后跑最小生成树。AT没有暴力分你想什么呢

性质2：增加的边权

既然不能直接跑最小生成树，思考如何优化。

思考我们平时跑 Kruscal 的过程。我们每次选择边权最短的边，判断其是否已经在一个连通块中，如果不在则选择这条边，否则忽略。

我们把“每一次边权+1”的限制应用到这里，可以这样操作：

首先把所有所有 $(A_i,B_i,C_i)$ 以 $C$ 为标准，从小到大排序。每次只使用前几个边，保证前几个边的 $C$ 值一定相等，对于这些边经进行和 Kruscal 一样的操作。使用完之后对 $A,B,C$ 进行相应的增加，如此操作，直到选择了 $n-1$ 个就结束了。

可能没有太理解，我们更形象的讲

如果我们三条边的权值分别是$C_1=4,C_2=4,C_3=7$，不管他们连接了什么，我们一定会先判断$C_1,C_2$着两条边，接着，这两个边会增加1，变成$C_1=5,C_2=5,C_3=7$，那么什么时候判断$C_3$？到$C_1=C_2=C_3$的时候就会开始判断$C_3$。

再结合我们提到的性质，因为每条边最多会被操作 $2n$ 次，因此我们对于每条边判断也不会超过 $2n$ 次。这样我们是不是就得到了 $O(m\log m+2n)$ 的算法了？并不是。由于可能有很多条边的边权都是一样的（尤其是在每次最小的边权还会增加的情况下），所以我们最劣的情况可能所有 $m$ 条边都扫一次，再都增加，再都扫一次。因此复杂度是$O(2mn)$。

性质三：重复的边

【NOTE：以下的计算都是在模 $n$ 意义下的】

虽然复杂度不尽人意，但是我们还是可以在这个基础上继续探索。我们把目光集中到每条边连接的点的变化 $(x,y)\to (x+1,y) \to (x+1,y+1)$上面。

在上面的判断下，我们最不想看到的情况就是很多边连接的两个点已经相互连通了，我们称之为“差边”。我们很想把这种“差边”都给扔掉。但是直接扔掉会导致它后面演变出来边无法被统计，而演变出来的边可能不是“差边”。

我们仔细想一下，有没“差边”演变出来的还是“差边”的情况？

实际上是有的。

我们假设现在有一个连接 $(x,y)$ 且边权为 $k$ 的边。目前发现 $(x,y)$ 已经连通了。通过 $x\to a \to b \to y$ 这样一条边联通的。这说明了，一定有这样几条边权不大于 $k$ 的边分别连接了 $(x,a),(a,b),(b,y)$。那么我们观察 $(x+1,y+1)$，是不是同样一定会有几条边权不大于 $k+2$ 的边已经把 $(x+1,a+1),(a+1,b+1),(b+1,y+1)$ 连接了，即 $x+1\to a+1 \to b+1 \to y+1$已经被连接。

这里感性理解就是，你比人家慢一步，你前进一步，别人前进一步，你还是比人家慢一步。

所以我们发现一个“差边”，他后面 $(x+p,y+p)$ 都是“差边”。

小策略：拆边

那么 $(x,y) \to (x+1,y)$ 这次变化呢？我们无法判断 $(x+1,y)$ 是否也是差的。

很简单，我们只想要 $x,y$ 同时增加。那么我们干脆吧这两种分开来！

也就是说，我们对于 $(A_i,B_i,C_i)$ 直接变成 $(A_i,B_i,C_i),(A_i+1,B_i,C_i+1)$，并且使其变化规律变为每次 $A,B$同时 $+1$ ，$C +2$。代码实现就是：

for(int i=1;i<=m;i++){
    int u,v,w;
    scanf("%lld%lld%lld",&u,&v,&w);
    alled[++toted]=(edge){u,v,w};
    alled[++toted]=(edge){(u+1)%n,v,w+1};
} 

这样的好处是什么？我们虽然要看 $2m$ 个边，但是一旦一个边有一次变差了，我们就可以立刻把它扔掉，所以最后最多是看 $4m$ 次。

这里实现的方法就很多了，我个人用的是链维护。

判断空

//ST=start,ED=end
if(nex[ST]==ED){
     pushfront(now);
     now++;
}

加入新的可用边，因为$C+2$所以可能有比现在边权还小的边，不过不用慌，最多也就小1，所以放到链首就好了

while(now<=toted&&alled[now].w<alled[nex[ST]].w){
    pushfront(now);
    now++;
}
while(now<=toted&&alled[now].w==alled[pre[ED]].w){
    pushback(now);
    now++;
}

然后就是正常的 Kruscal 操作。如果它是差的，就把它弹出去。否则更新其数据，并且把它调到链尾。

int tmp=nex[ST];
int u=alled[tmp].from,v=alled[tmp].to,w=alled[tmp].w;
if(find(u)==find(v)){
    popx(tmp);
} else {
    fa[find(u)]=find(v);
    ans+=w;
    conn++;
    alled[tmp].from+=1,alled[tmp].to+=1,alled[tmp].w+=2;
    alled[tmp].from%=n,alled[tmp].to%=n;
    popx(tmp);
    pushback(tmp);
}

最后输出 ans 就是答案