ARC122F

ARC122F

题意

给定 $n$ 个红点和 $m$ 个蓝点。对于一个在 $(x,y)$ 的蓝点，可以将其移动到 $(x',y')$，费用是曼哈顿距离。问最小费用使得每个红点的右上方都至少有 $k$ 个蓝点。

$n,m\le 10^5$，$k\le 10$

Sol

非常好的题。

先考虑红点本身的限制，如下图，显然对于本身存在偏序关系的两个红点，去在右上方的红点即可。这样分析完之后，留下的红点假设有 $n'$ 个，排序之后应该满足 $\forall i\in [2,n'],x_i > x_{i-1},y_i<y_{i-1}$

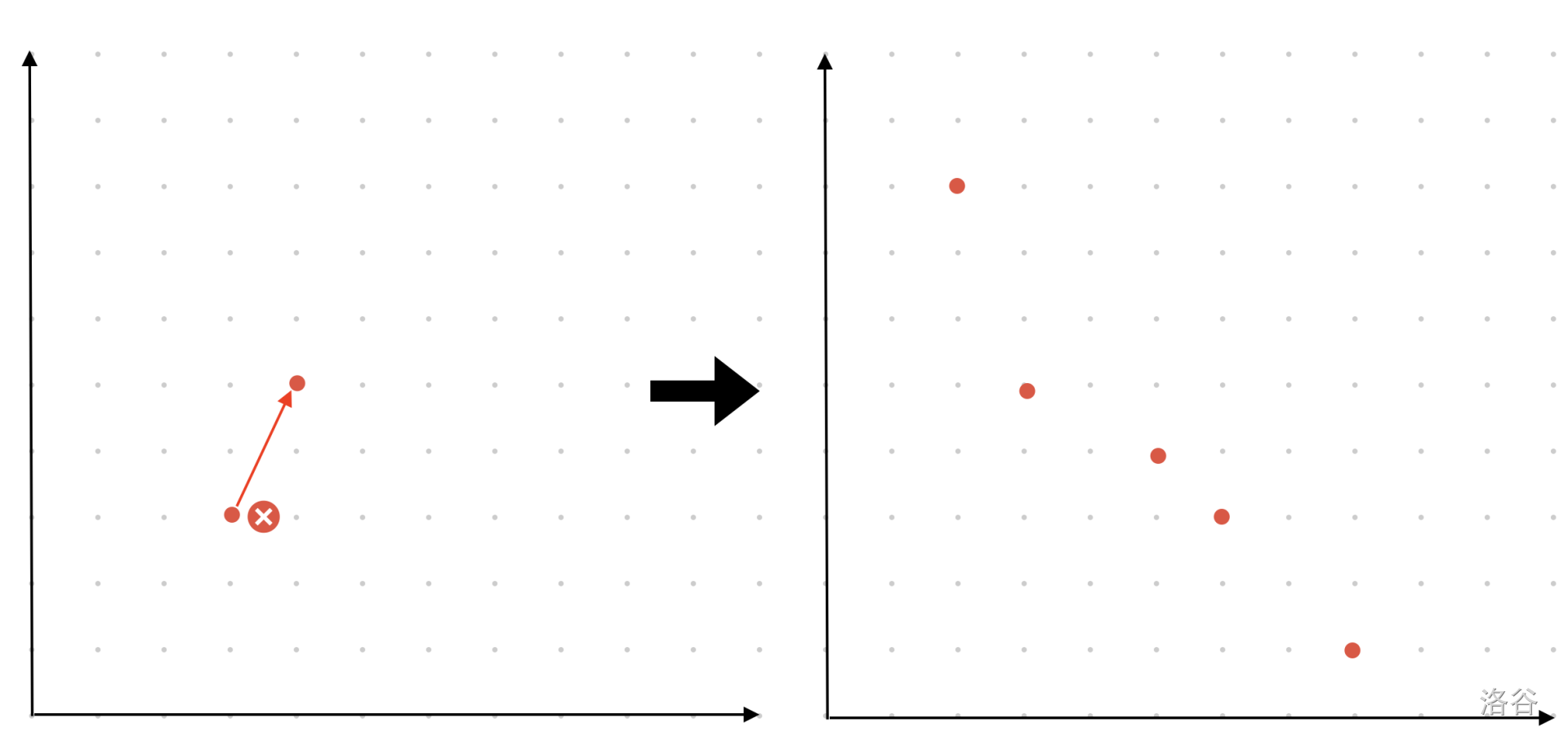
之后考虑蓝点，每个红点都被至少 $k$ 个蓝点覆盖，等价于将蓝点划分成 $k$ 组，每一个组都必须能够恰好覆盖到所有红点一次。这样做的好处是我们可以先考虑 $k=1$ 即所有蓝点恰好要覆盖所有红点至少一次。

我们先考虑不动的情况，相当于判断是否有解。这是一个经典的套路，对于每一个红点，连一条向上一个红点的边，对于一个蓝点，连一条向后的边。判断第一个红点能不能到达最后一个红点即可。如果不知道可能听起来有一点抽象，图如下（为了方便理解，图中所有蓝点 $(bx_i,by_i)$ 都存在 $rx_j=bx_i,ry_k=by_i$ 实际情况中需要建立一些虚拟的点）。

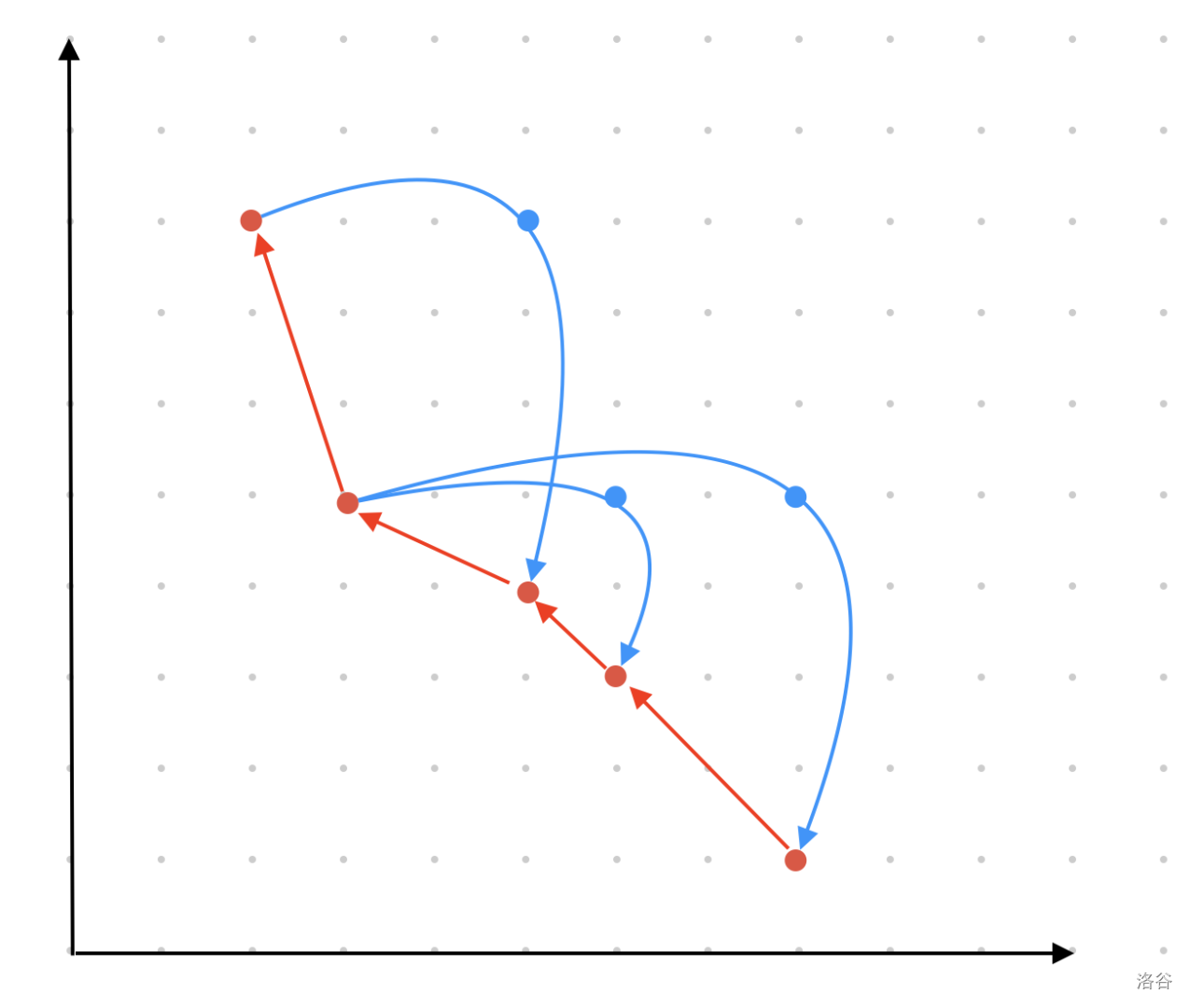
观察上面的过程，相当于一个人要从第一个点走到最后一个点。那么如果这个人到某个位置不能走了，此时就需要调整蓝点的位置了。首先显然蓝点只有往右或者往上调整才是有意义的。

但是维护蓝点的调整非常不方便，此时考虑在走路的那个人，可以把点的移动化成人的移动。将蓝点向上或者向右移动，就相当于人向下或者向右走（注意到是要从左上走到右下的）。

这时候就可以把需要移动点的问题变成，一个人从左上角的点出发，每个可以沿着图上已有的边走（红蓝边），代价为 $0$。或者往下走一格代价为 $1$ 或者往右走一格代价为 $1$，求此时走到终点的最短路。

看起来是不错的，但是这时候有一个比较大的问题，因为在二维平面，即使经过一定的离散化，点数仍然是爆炸的。考虑能不能变成一维的。

观察到红边其实就是一条链，这个和红点的具体位置是没有任何关系的，即不管红点怎么动，只要还满足排序的关系，红边是不会变的。蓝边其实只和红点的横纵坐标有关系，我们只关心这个红点是否是在蓝点的左下方，但其实也并不关心其具体的位置。这启发我们把每个点分别都摁到 $x$ 轴和 $y$ 轴上面。然后再考虑连边。

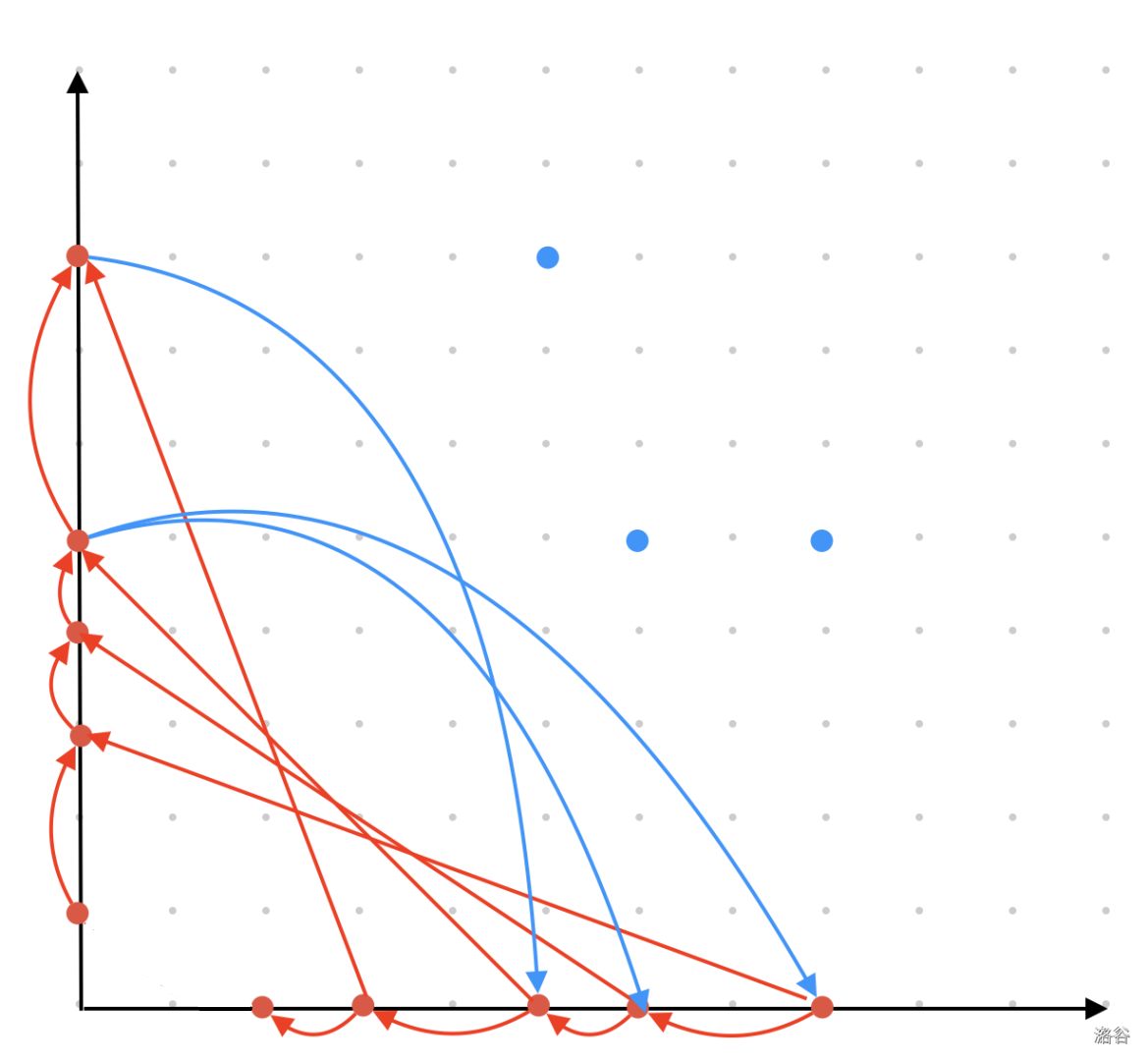
将每个点拆成两给再坐标轴上的点，此时从左上角的点到右下角的点的最短路就是答案。感性理解是显然的，证明的话可以考虑归纳，对于一个区间 $[l,r]$ 要满足从 $l$ 能够到 $r$ 是能够通过这样的构造成立的，之后进行推广。

注意图中没有画出来沿着 $y$ 轴向下和沿着 $x$ 轴向左的边。这些边同原来二维的情况，走是有代价的，其他边都没有代价。

这时候会发现点和边的数量都变为 $\mathcal{O}(n+m)$ 级别的了。

但是别忘记 $k$ 的限制。那么答案变得显然的，构造网络，从原点流一条到第一个点流量为 $k$ 的边。最后一个点流向汇点。其余所有边的流量为无限，给有边权的边加上费用即可。之后就是跑 MCMF。由于 $k$ 很小，这个题是可以通过的，直接 Dij + 原始对偶即可，复杂度是 $\mathcal{O}(k(n+m)\log (n+m))$ 的。

ATC 提交记录