一文可能看懂扫描线
扫描线入门
本文的文字部分有些冗长,有些地方讲的也有些枯燥,但是笔者已经尽量让文字不那么晦涩,也加了一些配图,相信坚持看完的读者会有所收获
本文参考:https://blog.csdn.net/tomorrowtodie/article/details/52048323
矩形面积并
对于矩形\(A,B\),它们的面积并就是\(A \cup B\)的面积,多个矩形的情况可以类比一下。怎么求面积并呢?有一种想法是拿所有矩形面积之和减去多加了的部分的面积,但是多加的部分并不好求,因为要计算交点,还要知道重复部分到底重复了多少次;我们可以假想有一条与\(x\)轴平行的直线,从下往上扫,把面积并分割成多个部分,如下图所示,这样以来面积并就等于各个颜色的部分的面积之和,每个部分的高很容易求,只要把每个矩形的每个横向边(与\(x\)轴平行的边)的高度记录一下,排个序,做差就可以,关键在于怎么求每个部分的长度,这时,线段树又出场了(不知道线段树的话,这里是传送门)
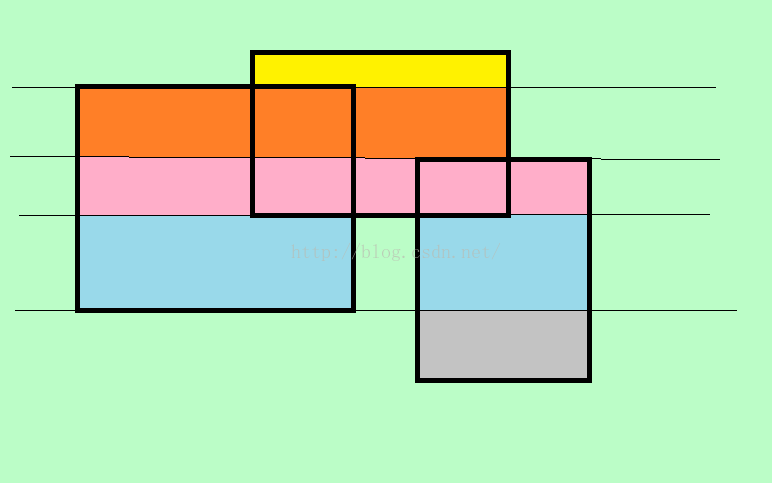
图片地址:https://blog.csdn.net/tomorrowtodie/article/details/52048323
区间信息
既然要用线段树,那线段树存什么?或者说要维护区间信息是什么?我们对横坐标区间建线段树,根节点的区间是\([x_{min}, x_{max}]\)(\(x\)是\(double\)咋整?可以离散化,下面会讲),即最左端的横坐标到最右端的横坐标,区间信息就是区间内有效的横向长度,这样每次拿高乘×根节点存的有效横向长度就能算出每个部分的面积,再累加就是答案了;那么要怎么维护区间信息呢?我们给每个区间维护一个\(cnt\),即目前该区间被横边覆盖的次数,怎么看这个目前呢?如果插入的是矩形下边界的横边,那被覆盖次数加一;相反,如果是上边界被覆盖次数减一。这样如果一个区间的\(cnt > 0\),说明该区间已经被完全覆盖了,那有效长度就等于区间长度;否则,如果\(cnt == 0\)(\(cnt\)不会小于0,除非你把下边界标记成上边界,上边界标记成下边界),那该区间的有效长度就是它的左儿子的有效长度加右儿子的(如果是叶子节点有效长度就是0),咱用下面的图模拟一下:
在这之前咱先讲讲,用到的结构体和数组定义,这样方便下文讨论。我们定义一个结构体\(Seg\)来表示矩形的上下边界(即横向边)以及结构体\(Node\)来表示线段树的各个节点;定义\(double\)数组\(corx\)存横坐标
const int N = 205; // 点数,即横向边的数量的两倍
struct Seg {
double l, r, h; // 左端点右端点和高度
int d; // 下边界的d==1,上边界的d==-1,你品,你细品
Seg() {}
Seg(double l, double r, double h, int d) : l(l), r(r), h(h), d(d) {}
inline bool operator < (const Seg& a) { // 用于将上下边界根据高度排序
return h < a.h;
}
} seg[N];
struct Node {
int l, r, cnt; // l和r要用到离散化技巧,之后会讲,cnt区间就是被覆盖次数
double sum; // 有效长度
} node[N << 2];
double corx[N];
(事先\(seg\)数组已经根据\(h\)排序)首先,对区间\([x_1, x_4]\)建线段树(这里的\(x\)坐标没排序),扫描线从\(h1\)开始,遇到第一个下边界\(x3x4\),并将它插入到线段树中,这时第一部分(下图灰色部分)的面积就等于\(node[1].sum*(seg[2].h - seg[1].h)\);而后,扫描线到达\(h2\),插入\(x1x2\),蓝色部分面积等于\(node[1].sum * (seg[3].h - seg[2].h)\),\(h3\)类似,到\(h4\)时,因为它是上边界,它会将\([x3,x4]\)部分的\(cnt\)值减1,然后计算红色部分面积,然后一步步算出总面积
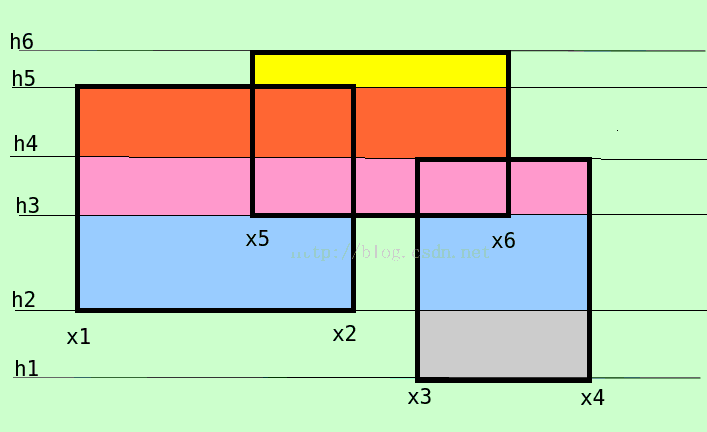
离散化
为啥要离散?
有两点原因:
- 有些题目给的坐标范围可能很大,比如\(1e9\),开数组必爆无疑
- 坐标可能还是\(double\),这样线段树不太好建立,想象一下区间端点是\(double\)型的线段树的叶子是个啥
(反正以笔者的水平是捣鼓不出来的)
怎么离散
我们可以不拿横坐标的值来当区间,而拿横坐标是从左往右的第几个来当区间,看图
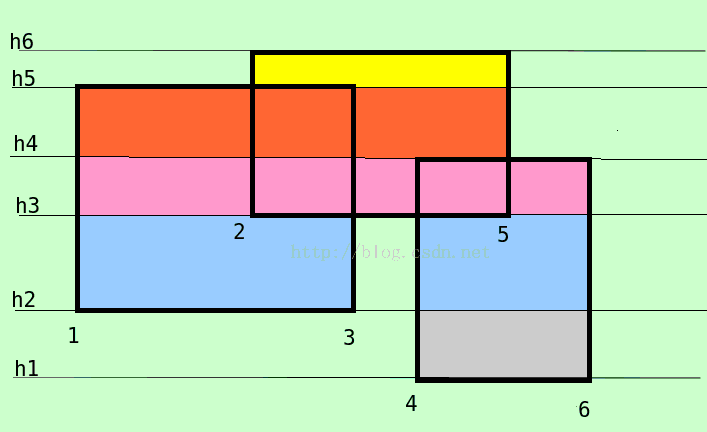
这样线段树的根节点的区间就缩小到\([1,N]\)了,可以存得下了,下面问题又来了,插入时怎么插?之前区间端点直接插入就得了,现在离散了咋整?因为我们已经对横坐标们排序,那我们用每条\(seg\)的左右端点的值通过\(lowerbound\)就能找到其在\(corx\)中对应的下标,这下就能快速插入了
亿点细节
心急的同学可能早就去看板子了(因为大家都会了),然而可能会有一些看不懂的奇怪细节:
- 上文说道如果一个区间的\(cnt>0\),那该区间的有效长度就是区间长度,但是现在离散化了,不能直接区间长度了,应该是坐标值之差
- 为啥板子71行\(x\)不减1,\(y\)减1?为啥\(update\)里\(node[k].r\)要加1,而\(node[k].l\)不加1?显然这两者是互相对应的,以下是笔者自己的见解,可能有错误,仅供参考:我们可以考虑一下,线段树的叶子节点,比如\(node[k].l == node[k].r == 1\)时,它的区间信息\(sum\)到底代表着什么,它应该代表的是从1开始,长度为1单位长度的区间内被覆盖的情况,那么从叶子节点向上,\(node[k']\)的区间信息\(sum\)代表的是从端点\(l\)开始,到端点\(r\)后,再往右1单位长度的这样区间的有效长度,所以\(y\)要减1,不然插入的区间就变成了\([x, y + 1]\)了;而\(update\)函数中的\(node[k].r + 1\)也解释得清楚了,但是读者们又要问了:那\(update\)里的\(else \ if\)那一行不应该是\(node[k].sum = 1\)吗?毕竟叶子节点代表的区间长度是1啊!叶子节点的区间长度确实是1,但是我们看上一句\(if\)的条件,只有在\(cnt == 0\)时,才有可能执行\(else \ if\)的语句,也就是说这时该区间的被覆盖次数为0,自然\(sum=0\)而不是\(1\),初始化的时候也一样,区间被覆盖次数为\(0\),自然\(sum = 0\)
void update(int k) {
if(node[k].cnt) node[k].sum = corx[node[k].r + 1] - corx[node[k].l]; // 区间被完全覆盖
else if(node[k].l == node[k].r) node[k].sum = 0; // 叶子
else node[k].sum = node[ls].sum + node[rs].sum;
}
71行:x = std::lower_bound(corx + 1, corx + sz + 1, seg[i].l) - corx;
y = std::lower_bound(corx + 1, corx + sz + 1, seg[i].r) - corx - 1;
照笔者这么说的话,线段树区间\([1, N-1]\)就够了,在HDU上确实也\(AC\)了(只测了下面的板子题),然而并不能说笔者的说法是正确的,所以还是建\([1, N]\)的树吧,毕竟仅仅测试了无数测试数据中的寥寥几组,仅作为一个参考
板子
#include <cstdio>
#include <algorithm>
#define ls (k << 1)
#define rs (ls | 1)
const int N = 205;
struct Seg {
double l, r, h;
int d;
Seg() {}
Seg(double l, double r, double h, int d) : l(l), r(r), h(h), d(d) {}
bool operator < (const Seg &a) const {
return h < a.h;
}
}seg[N];
struct Node {
int l, r, cnt;
double sum;
}node[N << 2];
int n, x, y, d;
double corx[N];
void build(int l, int r, int k) {
node[k].l = l; node[k].r = r; node[k].cnt = node[k].sum = 0;
if(l == r) return ;
int mid = (l + r) >> 1;
build(l, mid, ls);
build(mid + 1, r, rs);
}
void update(int k) {
if(node[k].cnt) node[k].sum = corx[node[k].r + 1] - corx[node[k].l]; // 区间被完全覆盖
else if(node[k].l == node[k].r) node[k].sum = 0; // 叶子
else node[k].sum = node[ls].sum + node[rs].sum;
}
void work(int k) {
if(node[k].l >= x && node[k].r <= y) {
node[k].cnt += d;
update(k);
return ;
}
int mid = (node[k].l + node[k].r) >> 1;
if(x <= mid) work(ls);
if(y > mid) work(rs);
update(k);
}
int main() {
int kase = 0;
while(~scanf("%d", &n)) {
if(!n) break;
for(int i = 1; i <= n; i++) {
double x1, x2, y1, y2;
scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
corx[i] = x1; corx[n + i] = x2;
seg[i] = Seg(x1, x2, y1, 1);
seg[i + n] = Seg(x1, x2, y2, -1);
}
n <<= 1;
std::sort(corx + 1, corx + n + 1);
std::sort(seg + 1, seg + n + 1);
int sz = std::unique(corx + 1, corx + n + 1) - corx - 1; // 去重
double ans = 0;
build(1, sz, 1);
for(int i = 1; i < n; i++) {
x = std::lower_bound(corx + 1, corx + sz + 1, seg[i].l) - corx;
y = std::lower_bound(corx + 1, corx + sz + 1, seg[i].r) - corx - 1;
d = seg[i].d;
work(1);
ans += (seg[i + 1].h - seg[i].h) * node[1].sum;
}
printf("Test case #%d\nTotal explored area: %.2f\n\n", ++kase, ans);
}
return 0;
}
例题
-
这题是求矩形并后的图形的周长,也是扫描线,之后专门再发一篇讲怎么算周长吧
暂时还没做多少例题(就是没做,之后再补点题,咕咕)

 浙公网安备 33010602011771号
浙公网安备 33010602011771号