李沐动手学深度学习8——softmax回归

对于多分类问题，用独热标签表示不同分类结果，比如对于三个结果A、B、C的分类问题，y属于{(0,0,1)、(0,1,0)、(1,0,0)}。

对于二分类问题，一般使用Sigmoid激活函数，输出一个范围是[0,1]的结果，输出层只需要单个神经元。

对于多分类问题（设n个分类），使用Softmax激活函数，为了估计所有可能类别的条件概率，模型需要有多个输出，输出层需要n个神经元。

对于多分类问题，由于计算任一输出均需要所有输入，因此其输出层是全连接层。

我们希望多分类问题的输出能代表在各个分类上的概率，非负且总和为1，因此使用softmax函数：

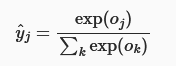
 softmax回归的输出由输入特征的仿射变换决定，因此，softmax回归是一个线性模型。

 

熵的定义

对于一个离散随机变量X，其概率分布是P(x)，熵H(x)的定义为：

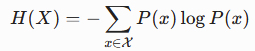
 直观理解：

易得若视 P(x) 为自变量，其取值范围为[0, 1]，则 logP(x) 的对应取值范围为(-∞,0]。

若是确定性事件，H(x) = -1*log1=0 。熵最小为0，对应事件完全确定

若是均匀分布事件，如掷骰子，H(x) = -6*(1/6)*log(1/6) = log6 。 熵越大对应事件越不可预测

 

交叉熵：

是用于分类任务的损失函数，定义为：

对于多分类任务，真实标签中，只有真实类别的yk值为1，其余为0，所以 L=-log(yk-hat)，预测值yk-hat越接近0，损失越大，越接近1，损失越小

对于二分类任务，其交叉熵损失函数简化可以写为

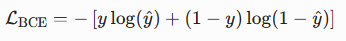
本质是多分类交叉熵函数的特殊形式

 

实践softmax回归时，使用的数据集是FashionMNIST，以下是数全部代码，运行时间较长：

import matplotlib.pyplot as plt
import torch
from torchvision import transforms
from torch.utils import data
import torchvision


def load_data_fashion_mnist(batch_size, resize=None):
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=False)
    mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=False)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False, num_workers=get_dataloader_workers()))


def get_dataloader_workers():
    return 4


def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]


def show_images(imgs, num_rows, num_cols, titles=None, scala=1.5):
    figsize = (num_cols * scala, num_rows * scala)
    fig, axes = plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            ax.imshow(img.numpy())
        else:
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes


def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(dim=1, keepdim=True)
    return X_exp/partition


def net(X):
    return softmax(torch.matmul(X.reshape(-1, W.shape[0]), W) + b)


def cross_entropy_loss(y_hat, y):
    # tensor切片接受两个列表分别作为行和列的传参
    return -torch.log(y_hat[range(len(y_hat)), y])


def accuracy(y_hat, y):
    # 若要将and换成&，需要给两边条件判断式加上括号，因为&优先级较高
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())


class Accumulator:
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]


def evaluate_accuracy(net, data_iter):
    if isinstance(net, torch.nn.Module):
        net.eval()
    metric = Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]


# 小批量梯度下降
def sgd(params, lr, batch_size):
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()


def updater(batch_size):
    return sgd([W, b], lr, batch_size)


def train_epoch_ch3(net, train_iter, loss, updater):
    if isinstance(net, torch.nn.Module):
        net.train()
    metric = Accumulator(3)
    for X, y in train_iter:
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 对优化器进行梯度清零会对所有参数进行梯度清零
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    return metric[0] / metric[2], metric[1] / metric[2]


def animator_display(xlabel, ylabel, legend, x, data):
    figsize = (12, 8)
    fig, axes = plt.subplots(figsize=figsize)
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    for i, data_item in enumerate(data):
        axes.plot(x, data_item, label=legend[i])
    axes.legend()
    plt.show()


def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
    data = [[], [], []]
    for epoch in range(num_epochs):
        print(epoch)
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        data[0].append(train_metrics[0])
        data[1].append(train_metrics[1])
        data[2].append(test_acc)
    animator_display(xlabel="epoch", ylabel="", legend=['train loss', 'train acc', 'test acc'],
                     x=range(1, num_epochs+1), data=data)


if __name__ == "__main__":
    _batch_size = 256
    num_input = 784
    num_output = 10
    lr = 0.1
    num_epochs = 10
    W = torch.normal(0, 0.01, size=(num_input, num_output), requires_grad=True)
    b = torch.zeros(num_output, requires_grad=True)
    train_iter, test_iter = load_data_fashion_mnist(_batch_size)
    train_ch3(net, train_iter, test_iter, cross_entropy_loss, num_epochs, updater)

    # 1.导入并查看fashion_mnist数据
    # X, y = next(iter(train_iter))
    # show_images(X.reshape(32, 64, 64), 4, 8, titles=get_fashion_mnist_labels(y))
    # plt.show()

    # 2.设计模型:
    # 神经网络层: 原始图片是28*28像素，在多类回归时先展平为长度784的一维向量，
    # 传入10个神经元的全连接层，激活函数是softmax
    # 损失函数为交叉熵损失
    # print(softmax(torch.tensor([[1, 2, 3], [3, 2, 1]])))

    # 精度计算测试
    # test_y_hat = torch.tensor([[0.1, 0.2, 0.3], [0.3, 0.2, 0.1]])
    # test_y = torch.tensor([2, 0])
    # print(accuracy(test_y_hat, test_y) / len(test_y))

    # 图像绘制测试
    # xlabel = "x"
    # ylabel = "y"
    # legend = ["A", "B", "C"]
    # x = range(1, 6)
    # y_data = [[0, 1, 1, 1, 1], [2, 2, 2, 2, 2], [3, 2, 1, 0, -1]]
    # animator_display(xlabel, ylabel, legend, x, y_data)