李沐动手学深度学习5——自动微分

李沐动手学深度学习，有视频、有中文电子书(含配套代码)，推荐！

视频（B站搜一大堆）：https://www.bilibili.com/video/BV1fsmyYnEfw?spm_id_from=333.788.videopod.episodes&vd_source=0199f117e2bdbb60970034d4f33ff67d

官网电子书：https://zh.d2l.ai/index.html

在机器学习里，矩阵计算比迭代计算效率更高。因此，需要学习矩阵微分求导：

———— 例子一 ——————————

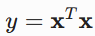  ：该函数对列向量X求导

首先展开该函数得

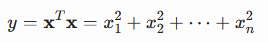
再对每个分量xi求偏导，得：

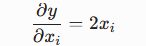
 得到梯度为：

 

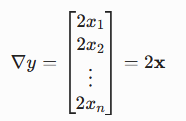
———— 例子二 ——————————

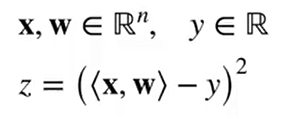：该函数 (线性回归代价，y是标量) 对向量w求导

即计算：

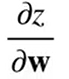
 由求导的链式法则，先设：

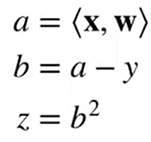
所以：

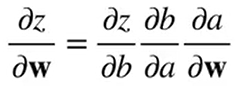
推出：

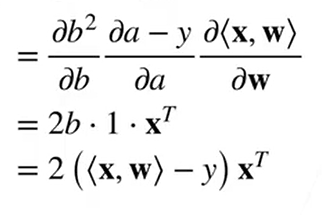
———— 例子三——————————

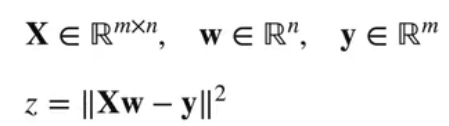：该函数 (y是标量，||是L2范数) 对向量w求导

同上用链式法则求导：

 

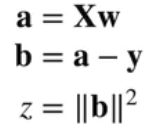
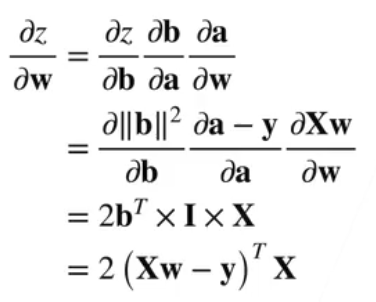
以上是矩阵微分求导的过程，实现自动求导的算法运用了链式法则的思想，通常基于计算图来实现

计算图：

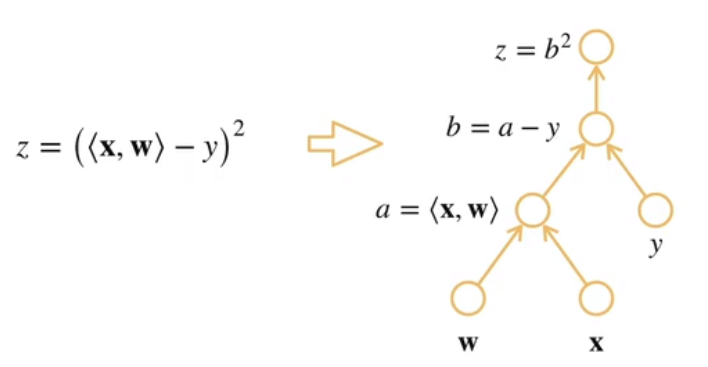
计算图将函数逐层分解为张量、张量操作和张量之间的依赖关系。

在进行自动求导计算时，可以使用两种方法：正向累积、反向累积（正向传播、反向传播）

如下图，可以这么理解正向和反向的区别：（上中下依次为链式法则、正向累积、反向累积）

 

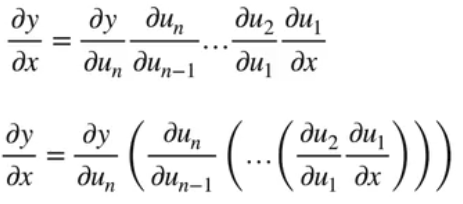
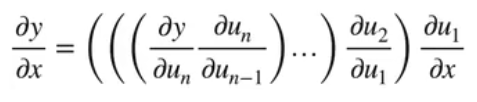
正向累积、反向累积求导的过程：

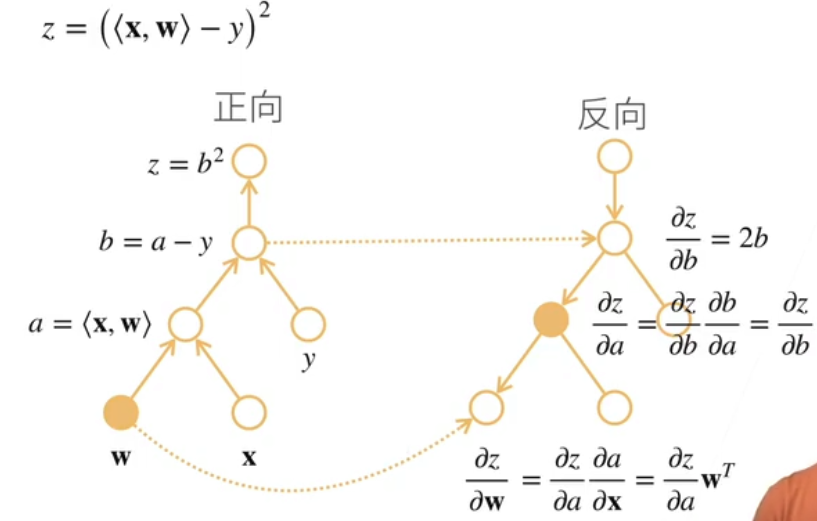
求线性回归代价梯度：

正向：a对x求导(累乘得xT) ——> b对a求导(累乘得xT) ——> z对b求导(累乘得2xT)

反向：z对b求导得2b(需要知道b的值) ——> z对a求导得2b ——> z对w求导得(需要知道x的值)

反向累积可以去除多余的枝，在反向累积前需要前向计算的中间结果

正向传播计算导数时，虽然不需要额外的内存存储中间结果，但对于输入向量中的每一个属性xi，都需要计算一遍y对其的偏导，效率较低

反向传播计算导数时，需要先完成一次正向传播并记录中间值，然后就能一次计算出梯度，内存消耗更大但效率更高

举例：

 

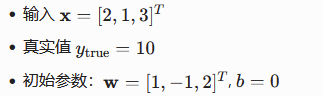
如果用正向传播的方法计算梯度：

即计算L对w的导数，L对w的偏导为(wx-y)x  ，对w中的n项，需要计算n次

 

如果用反向传播的方法计算梯度：

先计算出y和L的值分别是7和4.5，再计算L对y的导数，等于y-（y-true），等于-3

再计算y对w求导得x:(2,1,3) （还有常数项1），所以L对w求导得（-6，-3，-9）（还有b=-3）

 

原理结束，以下是代码实现，知识点是pytorch的反向传播梯度计算功能：

import torch

# 对y=2xTx关于x求导
x = torch.arange(4.0)
print(x)
x.requires_grad = True  # 等价于x=torch.arange(4.0,requires_grad=True)
print(x.grad)
y = 2 * torch.dot(x, x)
print(y)
# 反向传播函数backward
y.backward()
print(x.grad)

# pytorch默认累积梯度，计算新梯度前先清除之前的梯度
x.grad.zero_()
y = x.sum()
y.backward()
print(x.grad)

# 非标量变量的反向传播
x.grad.zero_()
y = x * x
# 先求和再算梯度
y.sum().backward()
print(x.grad)

# 使用detach函数将计算移动到计算图外
# detach函数: 从计算图中分离一个张量，返回一个新的不需要梯度的张量，同时共享原张量的内存
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
print(x.grad == u)  # 链式法则被阻断了
# 而原始张量y不受影响
x.grad.zero_()
y.sum().backward()
print(x.grad == 2*x)


# 计算图的记录在python控制流执行期间始终生效
def f(a):
    b = a*2
    while b.norm()<1000:
        b = b * 2
    if b.sum() > 0:
       c = b
    else:
        c = 100 * b
    return c


a = torch.randn(size = (), requires_grad = True)
d = f(a)
d.backward()
print(a.grad == d/a)