组合计数
前置
下面有些关于组合数的题可能需要额外用到关于乘法逆元的东西,详见 我的博客。如果说不想学的话,你可以先记住一个结论,对于一个质数 \(P\),满足 \(\dfrac{a}{b}\pmod{P}=a\times b^{P-2}\pmod{P}\)。
计数原理
加法原理和乘法原理
加法原理:
\(S=a_1+a_2+a_3+…+a_n\)。
乘法原理:
\(S=a_1\times a_2\times a_3\times …\times a_n\)。
习题:
\(1.\) P8557 炼金术(Alchemy)
每一种金属都可以被任意一个熔炉制造,每一个熔炉可以选择制第 \(i\) 个金属,也可以选择不制,因此有 \(2^k\) 中方案,但是必须得保证有一个熔炉制第 \(i\) 个金属,所以不能存在所有熔炉都不制的这一种情况,因此需要减去 \(1\),即制作第 \(i\) 个金属一共有 \(2^k-1\) 种方案。
一共有 \(n\) 个金属,每个金属都是如此,因此一共有 \((2^k-1)^n\) 种方案。
夜观天象,你就知道谁光芒万丈。
#include <iostream>
#include <cstdio>
#define ll long long
#define mod 998244353
using namespace std;
ll ksm(ll a,ll b){
ll res = 1;
while(b){
if(b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
int main(){
ll n,k;
scanf("%lld%lld",&n,&k);
printf("%lld",ksm(ksm(2,k) - 1,n));
return 0;
}
\(2.\) P5303 [GXOI/GZOI2019] 逼死强迫症
题解会在将来补充。
逍遥江湖,纵横四海。
#include <iostream>
#include <cstring>
#include <cstdio>
#define ll long long
#define mod 1000000007
using namespace std;
struct Matrix{
ll a[6][6];
inline Matrix(){memset(a,0,sizeof(a));}
inline Matrix operator * (const Matrix &x) const{
Matrix c;
for(int i = 1;i <= 5;i ++){
for(int j = 1;j <= 5;j ++){
for(int k = 1;k <= 5;k ++){
c.a[i][k] = (c.a[i][k] + a[i][j] * x.a[j][k]) % mod;
}
}
}
return c;
}
}s;
Matrix ksm(Matrix a,int b){
Matrix res;
res.a[1][1] = res.a[2][2] = res.a[3][3] = res.a[4][4] = res.a[5][5] = 1;
while(b){
if(b & 1) res = res * a;
b >>= 1;
a = a * a;
}
return res;
}
int main(){
s.a[1][2] = s.a[2][1] = s.a[2][2] = s.a[3][4] = s.a[4][3] = s.a[4][4] = s.a[5][5] = 1;
s.a[4][2] = 2,s.a[5][2] = mod - 1;
int T;scanf("%d",&T);
while(T --){
int n;
scanf("%d",&n);
if(n < 3) puts("0");
else{
Matrix ans;
ans.a[1][3] = 1,ans.a[1][4] = ans.a[1][5] = 2;
printf("%lld\n",(ans * ksm(s,n - 2)).a[1][2]);
}
}
return 0;
}
\(3.\) P8321 『JROI-4』沈阳大街 2
题解将在将来补充。
我李逍遥可以对天发誓,从今以后决不让你一人孤苦伶仃。
#include <algorithm>
#include <iostream>
#include <cstdio>
#define ll long long
#define mod 998244353
using namespace std;
bool cmp(int x,int y) {return x > y;}
ll ksm(ll a,ll b){
ll res = 1;
while(b){
if(b & 1) res = res * a % mod;
b >>= 1;
a = a * a % mod;
}
return res;
}
int n;ll a[5005],b[5005],f[10005][5005],cnt[10005],c[10005];
int main(){
scanf("%lld",&n);
for(int i = 1;i <= n;i ++) scanf("%lld",&a[i]);
for(int i = 1;i <= n;i ++) scanf("%lld",&b[i]);
sort(b + 1,b + n + 1,cmp);
int p = 1,q = 1,num = 0;
while(p <= n and q <= n){
if(a[p] >= b[q]) c[++num] = a[p],cnt[num] = q - 1,p ++;
else c[++num] = b[q],cnt[num] = p - 1,q ++;
}
while(p <= n) c[++num] = a[p],cnt[num] = q - 1,p ++;
while(q <= n) c[++num] = b[q],cnt[num] = p - 1,q ++;
for(int i = 0;i <= num;i ++) f[i][0] = 1;
for(int i = 1;i <= num;i ++){
for(int j = 1;j <= cnt[i];j ++){
f[i][j] = (f[i - 1][j - 1] * c[i] % mod * (cnt[i] - j + 1) % mod + f[i - 1][j]) % mod;
}
}
ll ans = 1;
for(int i = 1;i <= n;i ++) ans = ans * i % mod;
printf("%lld",f[num][n] * ksm(ans,mod - 2) % mod);
return 0;
}
组合数
组合数计算
递推
递推式:\(C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\)。
例题:P2822 [NOIP2016 提高组] 组合数问题
先通过递推式预处理出 \(C_i^j\bmod k\),然后利用二位前缀和思想预处理出答案,\(ans_{i,j} = ans_{i,j - 1} + ans_{i - 1,j} - ans_{i - 1,j - 1}\),如果 \(C_i^j\bmod k=0\),就再 \(+1\)。预处理方式详见代码。
魔非魔,道非道,善恶在人心。
#include <bits/stdc++.h>
#define N 2005
using namespace std;
int T,k,c[N][N],f[N][N],n,m;
void work(){
c[0][0] = c[1][0] = c[1][1] = 1;
for(int i = 2;i <= 2000;i ++){
c[i][0] = c[i][i] = 1;
for(int j = 1;j < i;j ++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % k;
}
for(int i = 1;i <= 2000;i ++){
for(int j = 1;j <= i;j ++){
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + (c[i][j] ? 0 : 1);
}
f[i][i + 1] = f[i][i];
}
}
void Input(){
while(T --){
scanf("%d%d",&n,&m);
if(m > n) printf("%d\n",f[n][n]);
else printf("%d\n",f[n][m]);
}
}
int main(){
scanf("%d%d",&T,&k);
work();
Input();
return 0;
}
习题:
\(1.\) P5239 回忆京都
相当于例题的变式,基本没什么不一样的,只不过预处理直接预处理和就行。注意让求的是 \(C_j^i\) 的和,所以最后输出的应该是 \(ans_{m,n}\)。
如果这是场梦,又该如何结束呢。
#include <bits/stdc++.h>
#define N 2005
#define MOD 19260817
using namespace std;
int T,c[N][N],f[N][N],n,m;
void work(){
c[0][0] = c[1][0] = c[1][1] = 1;
for(int i = 2;i <= 2000;i ++){
c[i][0] = c[i][i] = 1;
for(int j = 1;j < i;j ++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
for(int i = 1;i <= 2000;i ++){
for(int j = 1;j <= i;j ++){
f[i][j] = ((f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + c[i][j]) % MOD + MOD) % MOD;
}
f[i][i + 1] = f[i][i];
}
}
void Input(){
while(T --){
scanf("%d%d",&n,&m);
if(n > m) printf("%d\n",f[m][m]);
else printf("%d\n",f[m][n]);
}
}
int main(){
scanf("%d",&T);
work();
Input();
return 0;
}
阶乘
阶乘式:\(C_n^m=\dfrac{n!}{m!(n-m)!}\)。
利用阶乘式求解的话,即可以先处理处阶乘,然后利用乘法逆元求解。
Lucas 定理
Lucas 定理内容:
对于质数 \(p\),有\(C_n^m\bmod p=C_{\left\lfloor\dfrac{n}{p}\right\rfloor}^{\left\lfloor\dfrac{m}{p}\right\rfloor}\times C_{n\bmod p}^{m\bmod p}\bmod p\)。边界条件:当 \(m=0\) 时,返回 \(1\)。
注意:次定理必须满足 \(p\) 为质数,否则需要 exLucas 定理。而且也要求 \(p\) 的范围不宜过大,一般在 \(10^5\) 左右。
例题:P3807 【模板】卢卡斯定理/Lucas 定理
#include <bits/stdc++.h>
#define N 100005
#define int long long
using namespace std;
int T,p,a[N];
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % p;
b >>= 1;
a = a * a % p;
}
return res;
}
int C(int n,int m){
if(m > n) return 0;//一定要注意这里。
return a[n] * ksm(a[m] * a[n - m] % p,p - 2) % p;
}
int Lucas(int n,int m){
if(m == 0) return 1;
return Lucas(n / p,m / p) * C(n % p,m % p) % p;
}
signed main(){
scanf("%lld",&T);
int n,m;while(T --){
scanf("%lld%lld%lld",&n,&m,&p);
a[0] = 1;for(int i = 1;i <= p;i ++) a[i] = (a[i - 1] * i) % p;
printf("%lld\n",Lucas(n + m,n));
}
return 0;
}
习题:
\(1.\) P3773 [CTSC2017] 吉夫特
考虑 Lucas 定理,\(C_{a_i}^{a_j}=C_{{a_i}/2}^{{a_j}/2}\times C_{{a_i}\%2}^{{a_j}\%2}\)。
对于 \(C_{{a_i}\%2}^{{a_j}\%2}\),有四种情况,分别为 \(C_0^0,C_0^1,C_1^0,C_1^1\),其中只有 \(C_0^1=0\)。
然后我们发现,这个过程就相当于把 \(a_i\) 和 \(a_j\) 进行二进制拆位,只要出现 \(C_0^1\),那么 \(C_{a_i}^{a_j}\) 就为 \(0\),进而导致最终结果为 \(0\)。
也就是说二进制下不能存在某一位 \(a_i\) 为 \(0\) 而 \(a_j\) 为 \(1\),那么也就是当且仅当 \(a_j\) 在二进制下为 \(a_i\) 的子集。
我们设 \(f_i\) 为以 \(i\) 为结尾的子序列的个数,然后枚举子集转移即可。
下面解释什么叫二进制下的子集。
\(1011\) 的二进制子集有 \(1011,1010,1001,1000,0011,0010,0001,0000\),所以当 \(a_j\) 在二进制下为 \(a_i\) 的子集时,不存在某一位 \(a_i\) 为 \(0\) 而 \(a_j\) 为 \(1\)。
代码实现方式可以看代码 \(13\) 行的 for 循环,\(j\) 就相当于 \(a\) 在二进制下的子集,具体为什么可以这样写,可以子集手动模拟一下。
仰望夜空,你就知道我来自哪里。
#include <bits/stdc++.h>
#define N 233335
#define MOD 1000000007
using namespace std;
int n,a,ans,f[N];
int main(){
scanf("%d",&n);
for(int i = 1;i <= n;i ++){
scanf("%d",&a);
for(int j = (a - 1) & a;j;j = (j - 1) & a) f[j] = (f[j] + f[a] + 1) % MOD;
ans = (ans + f[a]) % MOD;
}
printf("%d\n",ans);
return 0;
}
二项式定理
二项式定理内容:
二项式定理阐明了一个展开式的系数:\(\begin{aligned}(a+b)^n=\sum\limits_{i=0}^nC_n^ia^ib^{n-i}\end{aligned}\)。
例题:P1313 [NOIP2011 提高组] 计算系数
根据二项式定理可得,\(\begin{aligned}(ax+by)^n=\sum\limits_{i=0}^nC_n^i(ax)^i(by)^{n-i}=\sum\limits_{i=0}^n(C_n^ia^ib^{n-i})x^iy^{n-i}\end{aligned}\)。
提醒:\(10007\) 为质数。
额上有疤的男人,个个都是传奇。
#include <bits/stdc++.h>
#define N 1005
#define MOD 10007
#define int long long
using namespace std;
int s[N];
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
int C(int x,int y) {return s[x] * ksm(s[y] * s[x - y] % MOD,MOD - 2) % MOD;}
signed main(){
int a,b,k,n,m;scanf("%lld%lld%lld%lld%lld",&a,&b,&k,&n,&m);
s[0] = 1;for(int i = 1;i <= k;i ++) s[i] = s[i - 1] * i % MOD;
int ans = ksm(a,n) * ksm(b,m) % MOD * C(k,n) % MOD;
printf("%lld",ans);
return 0;
}
排列组合应用
与加法原理和乘法原理结合。
习题:
\(1.\) P2606 [ZJOI2010] 排列计数
题意可以转化为:在 \(1\) 到 \(n\) 的所有排列中,满足小根堆性质的排列的个数。
注:小根堆是一颗完全二叉树,所以整个树的形态刚开始就是确定的,只要往里面插入值就行就行。小根堆的性质是,子节点 \(>\) 父亲节点。下面给出一颗小根堆:
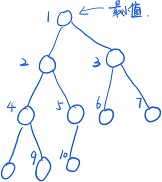
设 \(s_i\) 为节点 \(i\) 的子节点个数,包括自己,\(f_i\) 表示以 \(i\) 为根节点内的子树的方案数,那么 \(f_i = C_{s[i]-1}^{s[i\times 2]}\times f_{i\times 2}\times f_{i\times 2+1}\)。
可以理解为:对于每一棵子树对应一些数字,这些数字的最小值必须得在根结点上,然后任意选 \(s[i\times2]\) 个数放左子树里,其他放右子树里,把方案数相乘即可。
星光荡开宇宙,本人闪耀其中。
#include <bits/stdc++.h>
#define int long long
#define N 1000006
using namespace std;
int n,p,a[N],s[N << 1],f[N << 1];
int ksm(int x,int y){
int res = 1;
while(y){
if(y & 1) res = res * x % p;
y >>= 1;
x = x * x % p;
}
return res;
}
int C(int x,int y){
if(y > x) return 0;
return a[x] * ksm(a[y] * a[x - y] % p,p - 2) % p;
}
int Lucas(int x,int y){
if(y == 0) return 1;
return Lucas(x / p,y / p) * C(x % p,y % p) % p;
}
signed main(){
scanf("%lld%lld",&n,&p);
a[0] = 1;for(int i = 1;i <= n;i ++) a[i] = a[i - 1] * i % p;
for(int i = 1;i <= n;i ++) s[i] = 1;
for(int i = n;i >= 2;i --) s[i / 2] += s[i];
for(int i = n + 1;i <= n * 2 + 1;i ++) f[i] = 1;
for(int i = n;i >= 1;i --) f[i] = Lucas(s[i] - 1,s[i * 2]) * f[i * 2] % p * f[i * 2 + 1] % p,cout << i << " " << s[i] << " " << s[i * 2] << " " << f[i] << endl;
printf("%lld",f[1]);
return 0;
}
卡特兰数
卡特兰数是组合数学中一个常用数列,在数数题中屡见不鲜。其下标从 \(0\) 开始,前几项依次为 \(1,1,2,5,14,42,132…\)(其实可以稍微记一下,有助于我们在一些不知道的题目中通过暴力来寻找规律)。
前置知识
在平面直角坐标系中,从 \((0,0)\) 走到 \((n,n)\),只能向右或者向上走,问有多少种方案数?
容易知道,我们需要走 \(2n\) 步,其中有 \(n\) 步是向上走的,因此我们需要在 \(2n\) 步里面选出 \(n\) 步来向上走,即 \(C_{2n}^n\) 种方案数。简单推广一下,从 \((0,0)\) 走到 \((n,m)\),只能向右或者向上走,一共有 \(C_{n+m}^{n}\) 种方案数。
典例
这里举一个经典的例子——折线问题来阐述卡特兰数的意义:
在平面直角坐标系中,从 \((0,0)\) 走到 \((n,n)\),只能向右或者向上走一个单位长度,且不能穿过直线 \(y=x\)(注:可以触碰到 \(y=x\),但不能穿过)。请问一共有多少种走的方法?
我们定义 \(H_n\) 表示折线问题中从 \((0,0)\) 走到 \((n,n)\) 的方案数。
我们研究它的递推式。考虑枚举它在到达 \((n,n)\) 前走到的最后一个 \(y=x\) 上的点,设其为 \((i,i)\),那么到达这个点之前可以随意按照规则走,方案数为 \(H_i\),到达这个点后不能碰到直线 \(y=x\),相当于我们需要从 \((i+1,i)\) 走到 \((n,n-1)\),中间不能穿过 \(y=x-1\),稍微转换一下我们就容易知道这个的方案数为 \(H_{n-i-1}\)。于是我们就可以得到卡特兰数的一个递推式:\(H_n=H_0\times H_{n-1}+H_1\times H_{n-2}+…+H_{n-1}\times H_0,H_0=0\)。
这个的时间复杂度是 \(O(n^2)\) 的,那可不可以找到更快的方法?
可以试着求出来卡特兰数的通项公式。我们发现不穿过 \(y=x\) 这条线很难处理,我们考虑对其进行容斥,那么 \(H_n\) 就是总方案数,即 \(C_{2n}^n\) 减去穿过 \(y=x\) 路径的条数。但是穿过 \(y=x\) 的路径的条数看上去依然不是很好求。但是我们发现,穿过 \(y=x\) 的路径必定有一个点在 \(y=x+1\) 上,突发奇想,我们找到这样的第一个点,把它后面的路径翻转。
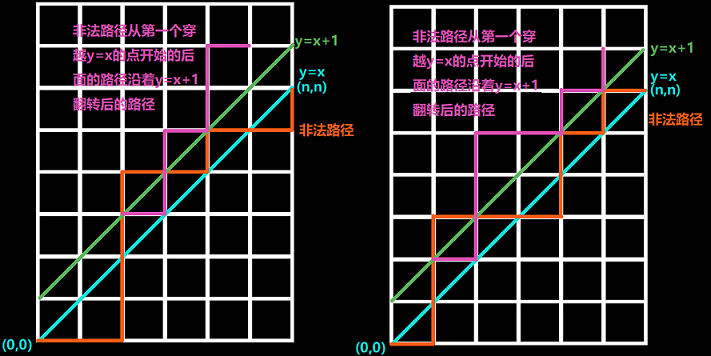
可以看出,翻转后的终点就变成了 \((n-1,n+1)\),并且我们可以发现,每一个非法路径都可以对应一个从 \((0,0)\) 到 \((n-1,n+1)\) 的路径,同样每一个从 \((0,0)\) 到 \((n-1,n+1)\) 的路径也都对应着一个非法路径,所以说非法路径的方案为 \(C_{2n}^{n-1}\)。由此可以得到卡特兰数的通项公式:\(H_n=C_{2n}^n-C_{2n}^{n-1}\)。
其实还有别的递推式和通项公式,不太常用,可以看下面。
卡特兰数列递推式和递推关系解:
令 \(H_n\) 为卡特兰数列第 \(n\) 项,令 \(H_0=1,H_1=1\),卡特兰数满足:
递推式:\(H_n=H_0\times H_{n-1}+H_1\times H_{n-2}+…+H_{n-1}\times H_0,H_0=0\)。
另类递推式:\(H_n=\dfrac{H_{n-1}\times (4n-2)}{n+1}\)。
递推关系的解:\(H_n=\dfrac{C_{2n}^n}{n+1}\)。
另类递推关系的解:\(H_n=C_{2n}^n-C_{2n}^{n-1}\)。
卡特兰数应用:详见 OI-wiki
习题:
\(1.\) P1722 矩阵 II P1044 [NOIP2003 普及组] 栈 P1976 鸡蛋饼 P1754 球迷购票问题 P1375 小猫 P2532 [AHOI2012] 树屋阶梯
注:以上全是纯板,反正就是 \(C_{2n}^n-C_{2n}^{n-1}\),不过 \(P2532\) 需要用到高精度
\(2.\) P1641 [SCOI2010] 生成字符串
就是稍微变形一下,公式是 \(C_{n+m}^m-C_{n+m}^{m-1}\)。
既不回头,何必不忘;既然无缘,何须誓言。
#include <iostream>
#include <cstdio>
#define N 2000006
#define MOD 20100403
#define int long long
using namespace std;
int n,m,a[N];
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
int C(int x,int y) {return a[x] * ksm(a[y] * a[x - y] % MOD,MOD - 2) % MOD;}
signed main(){
scanf("%lld%lld",&n,&m);
a[0] = 1;for(int i = 1;i <= n + m;i ++) a[i] = a[i - 1] * i % MOD;
int ans = (C(n + m,m) - C(n + m,m - 1) + MOD) % MOD;
printf("%lld",ans);
return 0;
}
\(3.\) P3200 [HNOI2009] 有趣的数列
转换一下题意:依次将 \(1\) 到 \(2n\) 放入一个序列,每次要么放在这个数列奇数位第一个没有数字的位置,要么放在这个数列偶数位第一个没有数字的位置,并且要满足奇数位当前存在的数的个数不多于偶数位数的个数。然后这不就转化为卡特兰数了吗?
注意:此题 \(p\) 不一定为质数,所以只能使用公式 \(H_n=\dfrac{C_{2n}^n}{n+1}=\dfrac{\prod\limits_{i=n+2}^{2n}i}{\prod\limits_{i=1}^ni}\)。
然后我们可以把 \(2n\) 之内的质数晒出来,同时得到每个数的最小质因数,统计每个质因子的个数然后使用使用快速幂计算。
一切都是冥冥之中的安排吗?
#include <bits/stdc++.h>
#define N 2000006
#define int long long
using namespace std;
int Prime[N],cnt,tot[N],n,MOD,ans = 1,vis[N];
void getPrime(){
for(int i = 2;i <= n * 2;i ++){
if(!vis[i]) Prime[++cnt] = i,vis[i] = i;
for(int j = 1;j <= cnt and i * Prime[j] <= n * 2;j ++){
vis[i * Prime[j]] = Prime[j];
if(i % Prime[j] == 0) break;
}
}
}
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
signed main(){
scanf("%lld%lld",&n,&MOD);getPrime();
for(int i = 1;i <= n;i ++) tot[i] = -1;//除以分母
for(int i = n + 2;i <= n * 2;i ++) tot[i] = 1;//乘以分子
for(int i = n * 2;i > 1;i --){
if(vis[i] < i){//如果是合数,就向下传递
tot[vis[i]] += tot[i];
tot[i / vis[i]] += tot[i];
}
}
for(int i = 2;i <= n * 2;i ++) if(vis[i] == i) ans = ans * ksm(i,tot[i]) % MOD;//如果是质数,就统计答案
printf("%lld",ans);
return 0;
}
什么?你不会筛质数?戳这里。
\(4.\) P5014 水の三角(修改版)
先咕着,后续会补上。
\(5.\) P3266 [JLOI2015] 骗我呢
题解 (先咕着,后续我会自己补上)
多项式与生成函数基础
拉格朗日插值
引入:
拉格朗日插值是沟通多项式的系数形式与点值形式的重要公式。众所周知 \(n+1\) 个 \(x\) 坐标不同的点可以确定唯一的最高为 \(n\) 次的多项式。然后题目中会给你 \(n+1\) 个点,然后让你求出它所构造出来的多项式在某一位置取值,这个时候可以利用拉格朗日法求解。拉格朗日插值公式:\(\begin{aligned}f(x)=\sum\limits_{i=1}^ny_i\prod\limits_{j\ne i}\dfrac{x-x_j}{x_i-x_j}\end{aligned}\)。
例题:P4781 【模板】拉格朗日插值
假设该多项式为 \(f_x\),第 \(i\) 个点的坐标为 \((x_i,y_i)\),求该多项式在 \(x=k\) 时的取值。
则 \(\begin{aligned}f_k=\sum\limits_{i=1}^ny_i\prod\limits_{i\ne j}\dfrac{k-x_j}{x_i-x_j}\end{aligned}\)。
证明不知道,自己搜索资料吧。时间复杂度 \(O(n^2)\)
#include <bits/stdc++.h>
#define N 2005
#define MOD 998244353
#define int long long
using namespace std;
int n,k,x[N],y[N],ans;
void Input(){
scanf("%lld%lld",&n,&k);
for(int i = 1;i <= n;i ++) scanf("%lld%lld",&x[i],&y[i]);
}
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
void work(){
for(int i = 1;i <= n;i ++){
int a = y[i],b = 1;
for(int j = 1;j <= n;j ++){
if(i == j) continue;
a = a * (k - x[j]) % MOD;
b = b * (x[i] - x[j]) % MOD;
}
a = (a + MOD) % MOD,b = (b + MOD) % MOD;
ans = (ans + a * ksm(b,MOD - 2)) % MOD;
}
printf("%lld",ans);
}
signed main(){
Input();
work();
return 0;
}
横坐标是连续整数的拉格朗日插值
设要求的 \(n-1\) 次多项式为 \(f(x)\),我们已知 \(f(1),f(2),…,f(n)\),则:
\(\begin{aligned}f(x)=\sum\limits_{i=1}^ny_i\prod\limits_{i\ne j}\dfrac{x-x_j}{x_i-x_j}=\sum\limits_{i=1}^ny_i\prod\limits_{i\ne j}\dfrac{x-j}{i-j}\end{aligned}\)。
此时,后面累乘的分子 \(=\dfrac{\begin{aligned}\prod\limits_{j=1}^n(x-j)\end{aligned}}{x-i}\),分母 \(=(-1)^{n-i}\times (i-1)!\times (n-i)!\)。
于是横坐标为 \(1,…,n\) 的插值公式 \(\begin{aligned}f(x)=\sum\limits_{i=1}^{n}y_i\dfrac{\prod\limits_{j=1}^{n}(x-j)}{(x-i)\times(-1)^{n-i}\times (i-1)!\times (n-i)!}\end{aligned}\)。
对于分子来说,然后我们可以预处理出关于 \(j\) 的前缀积和后缀积,即 \(\begin{aligned}pre_i=\prod\limits_{j=1}^i(x-j),nxt_i=\prod\limits_{j=i}^n(x-j)\end{aligned}\)。
对于分母来说,我们可与预处理出阶乘,即 \(fac_i=i!\)。
于是插值公式就变为 \(\begin{aligned}f(x)=\sum\limits_{i=1}^ny_i·(-1)^{n-i}·\dfrac{pre_{i-1}\times nxt_{i+1}}{fac_{i-1}\times fac_{n-i}}\end{aligned}\)。
经典应用:CF622F The Sum of the k-th Powers
\(\begin{aligned}\sum\limits_{i=1}^n i^k\end{aligned}\) 是一个 \(k+1\) 次多项式,具体怎么证明这个东西,自己可以看 这个题洛谷题解的第一篇。
然后这个题就基本搞定了,我们利用横坐标是连续整数的拉格朗日插值法,预处理出 \(\begin{aligned}\forall i\le k+2,\sum\limits_{j=1}^i j^k\end{aligned}\) 的值,也就是 \(y_i\),然后再根据上面的思路求解即可。
#include <bits/stdc++.h>
#define N 1000006
#define int long long
#define MOD 1000000007
using namespace std;
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
int n,k,a[N],y[N],pre[N],nxt[N],fac[N],ans;
signed main(){
scanf("%lld%lld",&n,&k);
for(int i = 1;i <= k + 2;i ++) a[i] = ksm(i,k);
for(int i = 1;i <= k + 2;i ++) y[i] = (y[i - 1] + a[i]) % MOD;
pre[0] = 1;for(int i = 1;i <= k + 2;i ++) pre[i] = pre[i - 1] * (n - i) % MOD;
nxt[k + 3] = 1;for(int i = k + 2;i >= 1;i --) nxt[i] = nxt[i + 1] * (n - i) % MOD;
fac[0] = 1;for(int i = 1;i <= k + 2;i ++) fac[i] = fac[i - 1] * i % MOD;
for(int i = 1;i <= k + 2;i ++){
int fm = pre[i - 1] * nxt[i + 1] % MOD;
int fz = ksm(fac[i - 1] * fac[k + 2 - i] % MOD,MOD - 2) % MOD;
ans += ((k + 2 - i) % 2 == 0 ? 1ll : -1ll) * y[i] * fm % MOD * fz % MOD;
ans = (ans % MOD + MOD) % MOD;
}
printf("%lld",ans);
return 0;
}
习题:
\(1.\) P4593 [TJOI2018] 教科书般的亵渎
我们可以通过 \(m\) 数值较小时的情况来推出通式。
当 \(m=1\) 时:
此时需要两张亵渎才能消灭所有随从。
第一次亵渎贡献的分数为 \(\begin{aligned}\sum\limits_{i=1}^ni^2-(a_1)^2\end{aligned}\)。
第二次亵渎贡献的分数为 \(\begin{aligned}\sum\limits_{i=1}^{n-a_1}i^2\end{aligned}\)。
当 \(m=2\) 时:
此时需要三张亵渎才能消灭所有随从。
第一次亵渎贡献的分数为 \(\begin{aligned}\sum\limits_{i=1}^ni^3-(a_1)^3-(a_2)^3\end{aligned}\)。
第二次亵渎贡献的分数为 \(\begin{aligned}\sum\limits_{i=1}^{n-a_1}i^3-(a_2-a_1)^3\end{aligned}\)。
第三次亵渎贡献的分数为 \(\begin{aligned}\sum\limits_{i=1}^{n-a_2}i^3\end{aligned}\)。
自己手动模拟一下即可。
由此,我们就可以推出通式为:(注意,先把 \(a_i\) 从小到大排序)
定义 \(a_0=0\),有\(\begin{aligned}ans=\sum\limits_{i=0}^{m}(\sum\limits_{j=1}^{n-a_i}j^{m+1}-\sum\limits_{j=i+1}^m(a_j-a_i)^{m+1})\end{aligned}\)。
到了这里就基本转化为板子题了,不过多解释。
生而无畏,战至终章。
#include <bits/stdc++.h>
#define N 60
#define int long long
#define MOD 1000000007
using namespace std;
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
int T,n,m,a[N],s[N],y[N],pre[N],nxt[N],fac[N],ans;
signed main(){
scanf("%lld",&T);while(T --){
scanf("%lld%lld",&n,&m);ans = 0;
for(int i = 1;i <= m + 3;i ++) s[i] = ksm(i,m + 1);
for(int i = 1;i <= m + 3;i ++) y[i] = (y[i - 1] + s[i]) % MOD;
fac[0] = 1;for(int i = 1;i <= m + 3;i ++) fac[i] = fac[i - 1] * i % MOD;
for(int i = 1;i <= m;i ++) scanf("%lld",&a[i]);sort(a + 1,a + m + 1);
for(int i = 0;i <= m;i ++){
pre[0] = 1;for(int j = 1;j <= m + 3;j ++) pre[j] = pre[j - 1] * (n - a[i] - j) % MOD;
nxt[m + 4] = 1;for(int j = m + 3;j >= 1;j --) nxt[j] = nxt[j + 1] * (n - a[i] - j) % MOD;
for(int j = 1;j <= m + 3;j ++){
int fm = pre[j - 1] * nxt[j + 1] % MOD;
int fz = ksm(fac[j - 1] * fac[m + 3 - j] % MOD,MOD - 2) % MOD;
ans += ((m + 3 - j) % 2 == 0 ? 1ll : -1ll) * y[j] * fm % MOD * fz % MOD;
ans = (ans % MOD + MOD) % MOD;
}
for(int j = i + 1;j <= m;j ++){
ans -= ksm(a[j] - a[i],m + 1);
ans = (ans % MOD + MOD) % MOD;
}
}
printf("%lld\n",ans);
}
return 0;
}
\(2.\) P3270 [JLOI2016] 成绩比较
先咕着,后续会补上。
\(3.\) P4463 [集训队互测 2012] calc
先咕着,后续会补上。
重心拉格朗日插值法
如果每次加入一个数都重新求多项式的插值,每次都是 \(O(n^2)\),不优。重心拉格朗日插值法可以再加入一个数后 \(O(n)\) 求出新的多项式的值。
\(\begin{aligned}f(x)=\sum\limits_{i=1}^ny_i\prod\limits_{j\ne i}\dfrac{x-x_j}{x_i-x_j}=\sum\limits_{i=1}^ny_i\dfrac{\prod\limits_{j=1}^n(x-x_j)}{(x-x_i)\times \prod\limits_{j\ne i}(x_i-x_j)}\end{aligned}\)。
令 \(\begin{aligned}S=\prod\limits_{j=1}^n(x-x_j),t_i=\dfrac{y_i}{\prod\limits_{j\ne i}(x_i-x_j)}\end{aligned}\)。
则原式转换为 \(\begin{aligned}f(x)=S\sum\limits_{i=1}^n\dfrac{t_i}{x-x_i}\end{aligned}\)。
然后每次加入一个新的点的时候,更新 \(S\) 和前 \(n\) 个点的 \(t_i\),并计算出新的 \(t_{i+1}\),然后按照次公式求和一遍即可得到新的多项式的值。
组合杂项
错排数
例题:P1595 信封问题
错排的递推式为 \(f_i=\begin{cases}0,if\ i=1\\1,if\ i = 2\\(i-1)\times (f_{i-1}+f_{i-2}),otherwise\\\end{cases}\)\(\pmod{P}\)
简单证明:将错排问题理解为,有 \(n\) 个颜色的球,\(n\) 个颜色的箱子,\(n\) 个颜色都对应着一个球和一个箱子,不能让一个球放进同一个颜色的箱子里,问有多少种方案。
假设我们将 \(n\) 号球放进了 \(k\) 号箱子 \((1\le k\le n-1)\):
如果此时我们把 \(k\) 号球放进了 \(n\) 号箱子,那么此时的方案数相当于剩下 \(n-2\) 个箱子的方案数,即 \(f_{n-2}\)。
如果此时我们不把 \(k\) 号球放进 \(n\) 号箱子,我们可以这样理解:\(k\) 号球不能与 \(n\) 号箱子匹配,其他除 \(k,n\) 之外的球不能与其对应颜色的箱子匹配,那么方案数相当于 \(n-1\) 个箱子的方案数,即 \(f_{n-1}\)。
由于 \(k\) 的取值个数为 \(n-1\) 个,所以 \(f_n=(n-1)\times (f_{n-1}+f_{n-2})\)。由此可以推得递推式。
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,f[22];
signed main(){
scanf("%lld",&n);
f[1] = 0,f[2] = 1;
for(int i = 3;i <= n;i ++) f[i] = (i - 1) * (f[i - 1] + f[i - 2]);
printf("%lld\n",f[n]);
return 0;
}
习题
\(1.\) P4071 [SDOI2016] 排列计数
对于 \(m\) 个位置为 \(i\) 的方案数为 \(C_n^m\),然后其他位置为错排,令 \(f_i\) 表示 \(i\) 个数的错排数,则最后结果为 \(C_n^m\times f_{n-m}\pmod{P}\)。注意本题需要额外规定 \(f_0=1\)。
点击查看代码
#include <bits/stdc++.h>
#define N 1000006
#define int long long
#define MOD 1000000007
using namespace std;
int T,n,m,s[N],f[N];
int ksm(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
signed main(){
s[0] = 1;for(int i = 1;i <= 1000000;i ++) s[i] = s[i - 1] * i % MOD;
f[0] = 1,f[1] = 0,f[2] = 1;for(int i = 3;i <= 1000000;i ++) f[i] = (i - 1) * (f[i - 1] + f[i - 2]) % MOD;
scanf("%lld",&T);while(T --){
scanf("%lld%lld",&n,&m);
int x = s[n] * ksm(s[n - m] * s[m] % MOD,MOD - 2) % MOD * f[n - m] % MOD;
printf("%lld\n",x);
}
return 0;
}
斐波那契数列
Prufer 序列
斯特林数
其它
贝尔数、伯努利数、分拆数、欧拉数。
都先咕着,啥时候想学了再回来补。

 剑指的方向,就是天才的故乡!
剑指的方向,就是天才的故乡!

 浙公网安备 33010602011771号
浙公网安备 33010602011771号