基础优化技巧1
二分
二分查找
略
二分答案
略
三分
定义:
三分法为二分法衍生出来的一种做法,可以求解一单峰函数或单谷函数的极值点。
注:单峰函数可以理解为,一函数中存在一个 \(x\),使得 \(∀x1<x,a_{x1} < a_{x}\), \(∀x2>x,a_{x2} > a_{x}\)。单谷函数则反之。
过程:
假设我们要找一个单谷函数的最小值:(想象一个开口向上的二次函数)
\((1)\) 任取定义域 \([l,r]\) 区间内的两点 \(lmid\) 和 \(rmid\)。
\((2)\) 若 \(a_{lmid}<a_{rmid}\),则可以舍弃定义域 \([rmid,r]\) 区间,并返回第一步。
\((3)\) 反之,则可以舍弃定义域 \([l,lmid]\) 区间,并返回第一步。
为了让复杂度降低,一般采取 \(lmid,rmid\) 为区间 \([l,r]\) 的两个三等分点。
例题:P3382 【模板】三分
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int n;
double l,r,a[20],d = 1e-10;
double check(double x){
double num = 0;
for(int i = 1;i <= n + 1;i ++) num += a[i] * pow(x,n + 1 - i);
return num;
}
int main(){
scanf("%d%lf%lf",&n,&l,&r);
for(int i = 1;i <= n + 1;i ++) scanf("%lf",&a[i]);
while(r - l > d){
double lmid = l + (r - l) / 3,rmid = r - (r - l) / 3;
if(check(lmid) > check(rmid) + d) r = rmid;
else l = lmid;
}
printf("%.5lf",(l + r) / 2);
return 0;
}
习题:
\(1.\) P1883 函数
双倍经验 Error Curves。
需要知道一个结论:如果 \(f(x),g(x)\) 为下凸函数,则 \(h(x)=max(f(x),g(x))\) 也是一个下凸函数。
想要得到娜可露露的吻吗?那就跟我做好朋友吧。
#include <bits/stdc++.h>
#define N 10004
#define max(a,b) a > b ? a : b
using namespace std;
const double d = 1e-9;
double a[N],b[N],c[N];int T,n;
double check(double x){
double res = -1e9;
for(int i = 1;i <= n;i ++) res = max(res,a[i] * x * x + b[i] * x + c[i]);
return res;
}
int main(){
scanf("%d",&T);while(T --){
scanf("%d",&n);
for(int i = 1;i <= n;i ++) scanf("%lf%lf%lf",&a[i],&b[i],&c[i]);
double l = 0,r = 1000;
while(r - l > d){
double lmid = l + (r - l) / 3,rmid = r - (r - l) / 3;
if(check(lmid) > check(rmid) + d) l = lmid;
else r = rmid;
}
printf("%.4lf\n",check(l));
}
return 0;
}
分治
简单分治
过程:
\((1)\) 将原问题分解成两个或多个具有相同结构的子问题。
\((2)\) 将子问题分解至可以简单求解的时候停止,求解答案后递归。
\((3)\) 将每一个子问题合并成原问题的答案。
例题:归并排序 P1908 逆序对
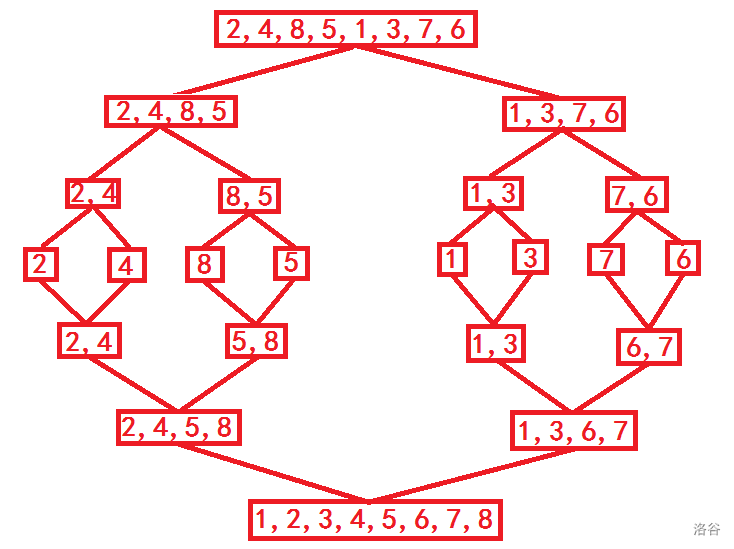
#include <iostream>
#include <cstdio>
using namespace std;
int a[500005];
int temp[500005];
long long ans;
void merge(int a[],int l,int mid,int r){
int i = l,j = mid + 1,k = l;
while(i <= mid and j <= r){
if(a[i] <= a[j]) temp[k ++] = a[i ++];
else ans += mid - i + 1,temp[k ++] = a[j ++];
}
while(i <= mid) temp[k ++] = a[i ++];
while(j <= r) temp[k ++] = a[j ++];
for(i = l;i <= r;i++) a[i] = temp[i];
}
void mergesort(int a[],int l,int r){
if(l < r){
int mid = l + (r - l) / 2;
mergesort(a,l,mid);
mergesort(a,mid + 1,r);
merge(a,l,mid,r);
}
}
int main(){
int n;
scanf("%d",&n);
for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
mergesort(a,1,n);
cout << ans;
return 0;
}
CDQ 分治
过程:
\((1)\) 找中点 \(mid\)。
\((2)\) 分别递归 \([l,mid],[mid+1,r]\)。
\((3)\) 处理 \(l\le i\le mid\) 与 \(l\le j\le mid\) 的贡献。
处理 \(mid+1\le i\le r\) 与 \(mid+1\le j\le r\) 的贡献。
处理 \(l\le i\le mid\) 与 \(mid+1\le j\le r\) 的贡献。
发现在我们递归过程中如果处理了第三种,就相当于处理了第一种和第二种,所以重点是在递归是如何处理第三种点对。
例题:P3810 【模板】三维偏序(陌上花开)
题目已经非常简洁明了了,这里直接讲解做法。
\((1)\) 以 \(a\) 为关键字对于序列进行从小到大排序,并把 \(a,b,c\) 三个属性都相同的元素合并到一个元素,并记录个数,方便后续树状数组的处理。
void Insert(){
sort(x + 1,x + n + 1,cmp1);
int top = 0;
for(int i = 1;i <= n;i ++){
top ++;
if(x[i].a != x[i + 1].a or x[i].b != x[i + 1].b or x[i].c != x[i + 1].c){
s[++ m].a = x[i].a,s[m].b = x[i].b,s[m].c = x[i].c,s[m].cnt = top;
top = 0;
}
}
}
\((2)\) (本题关键部分)转入 \(CDQ\) 函数并往下递归。递归到最底层时往上进行合并。合并记录答案的方法:
对于两边序列的元素分别以属性 \(b\) 为关键字进行排序(我们要知道,我们要找的时左右两个区间之间互相的贡献,而不是区间内部,所以此时左区间所有的 \(a\) 属性一定都小于右区间所有的 \(a\) 属性)。
然后以归并排序的方式以最低的复杂度找到 \(b_j\le b_i\) 的元素,并把 \(c_j\) 值加入树状数组(此时的树状数组相当于单点修改,区间查询的树状数组),紧接着记录树状数组中小于等于 \(c_i\) 值的元素有多少个,记录答案即可。并注意最终清空树状数组。
int lowbit(int x) {return x & (-x);}
void add(int x,int y){
while(x <= k){
c[x] += y;
x += lowbit(x);
}
}
int query(int x){
int sum = 0;
while(x){
sum += c[x];
x -= lowbit(x);
}
return sum;
}
void CDQ(int l,int r){
if(l == r) return ;
int mid = l + r >> 1;
CDQ(l,mid);CDQ(mid + 1,r);
sort(s + l,s + mid + 1,cmp2);
sort(s + mid + 1,s + r + 1,cmp2);
int i,j = l;
for(int i = mid + 1;i <= r;i ++){
while(s[i].b >= s[j].b and j <= mid){
add(s[j].c,s[j].cnt);
j ++;
}
s[i].ans += query(s[i].c);
}
for(i = l;i < j;i ++) add(s[i].c,- s[i].cnt);
}
\((3)\) 最后注意输出的是每个答案的数量,上文 \(s_{i_{ans}}\) 没有记录同 \(s_i\) 对应的 \(s_{i_{cnt}}-1\) 对应的这些数,所以最后需要简单处理一下。
void Output(){
for(int i = 1;i <= m;i ++) jilu[s[i].ans + s[i].cnt - 1] += s[i].cnt;
for(int i = 0;i < n;i ++) printf("%d\n",jilu[i]);
}
另外要格外注意 \(cmp1,cmp2\) 两者排序的方式,必须要逐一按照关键字排序!
bool cmp1(X a,X b){
if(a.a != b.a) return a.a < b.a;
if(a.b != b.b) return a.b < b.b;
if(a.c != b.c) return a.c < b.c;
}
bool cmp2(S a,S b){
if(a.b != b.b) return a.b < b.b;
if(a.c != b.c) return a.c < b.c;
}
我对你的第一印象很负面,但是没关系,我会尽力改变的。
#include <bits/stdc++.h>
#define N 100005
using namespace std;
struct X{int a,b,c;}x[N];
bool cmp1(X a,X b){
if(a.a != b.a) return a.a < b.a;
if(a.b != b.b) return a.b < b.b;
if(a.c != b.c) return a.c < b.c;
}
struct S{int a,b,c,cnt,ans;}s[N];
bool cmp2(S a,S b){
if(a.b != b.b) return a.b < b.b;
if(a.c != b.c) return a.c < b.c;
}
int n,m,K,c[N << 1],jilu[N];
void Input(){
scanf("%d%d",&n,&K);
for(int i = 1;i <= n;i ++) scanf("%d%d%d",&x[i].a,&x[i].b,&x[i].c);
sort(x + 1,x + n + 1,cmp1);int top = 0;
for(int i = 1;i <= n;i ++){
top ++;
if(x[i].a != x[i + 1].a or x[i].b != x[i + 1].b or x[i].c != x[i + 1].c){
s[++ m].a = x[i].a,s[m].b = x[i].b,s[m].c = x[i].c;
s[m].cnt = top,top = 0;
}
}
}
int lowbit(int x){return x & (-x);}
void add(int x,int y){
while(x <= K){
c[x] += y;
x += lowbit(x);
}
}
int query(int x){
int sum = 0;
while(x){
sum += c[x];
x -= lowbit(x);
}
return sum;
}
void CDQ(int l,int r){
if(l == r) return ;
int mid = l + r >> 1;
CDQ(l,mid),CDQ(mid + 1,r);
sort(s + l,s + mid + 1,cmp2);
sort(s + mid + 1,s + r + 1,cmp2);
int j = l;
for(int i = mid + 1;i <= r;i ++){
while(s[i].b >= s[j].b and j <= mid){
add(s[j].c,s[j].cnt);
j ++;
}
s[i].ans += query(s[i].c);
}
for(int i = l;i < j;i ++) add(s[i].c,-s[i].cnt);
}
void work(){
CDQ(1,m);
for(int i = 1;i <= m;i ++) jilu[s[i].ans + s[i].cnt - 1] += s[i].cnt;
for(int i = 0;i < n;i ++) printf("%d\n",jilu[i]);
}
int main(){
Input();
work();
return 0;
}
习题:
\(1.\) P3157 [CQOI2011] 动态逆序对
此题,我们先统计出初始逆序对的数量,然后再计算某一个数删除后对逆序对的影响。
对于这个序列与三维的限制,一个是下标 \(id\),一个是权值 \(a\),最后是被删除的时间 \(t\)。假设我们第一维按照 \(a\) 从大到小进行排序。那么:
对于一个权值,如果在他前面的数(前面的数的权值一定比它大)的 \(id\) 比它小,并且 \(t\) 比它大(删除时间晚),那么删除这个数的时候就会有影响(逆序对的个数 \(-1\))。
对于一个权值,如果在他后面的数(后面的数的权值一定比它小)的 \(id\) 比它大,并且 \(t\) 比它大(删除时间晚),那么删除这个数的时候就会有影响(逆序对的个数 \(-1\))。
这样就转化成了一个三维偏序问题。在递归过程中,对于每一个 \(l\le i\le mid,mid + 1\le j\le r\),依次处理删除左区间某一个数对于每一个右区间数的影响(此影响记录到左区间的那个数的删除时间),以及删除右区间某一个数对于每一个左区间数的影响(同理)。最后输出的时候让 \(num\) 依次减去当前时间的影响即可。
你们是我的眼中钉,我的肉中刺。
#include <bits/stdc++.h>
#define N 100005
#define M 50005
#define int long long
using namespace std;
int n,m,num,ans[N],c[M];
struct S{int a,id,t;}s[N],ls[N];
bool cmp1(S a,S b) {return a.id < b.id;}
bool cmp2(S a,S b) {return a.id > b.id;}
void mergesort(int l,int mid,int r){
int x = l,y = mid + 1,cnt = l;
while(x <= mid and y <= r){
if(s[x].a < s[y].a) ls[cnt ++] = s[y],y ++;
else ls[cnt ++] = s[x],x ++,num += r - y + 1;
}
while(x <= mid) ls[cnt ++] = s[x],x ++;
while(y <= r) ls[cnt ++] = s[y],y ++;
for(int i = l;i <= r;i ++) s[i] = ls[i];
}
void merge(int l,int r){
if(l == r) return ;
int mid = l + r >> 1;
merge(l,mid);merge(mid + 1,r);
mergesort(l,mid,r);
}
int lowbit(int x) {return x & (-x);}
void add(int x,int y){
while(x){
c[x] += y;
x -= lowbit(x);
}
}
int query(int x){
int res = 0;
while(x <= 50000){
res += c[x];
x += lowbit(x);
}
return res;
}
void CDQ(int l,int r){
if(l == r) return ;
int mid = l + r >> 1;
CDQ(l,mid),CDQ(mid + 1,r);
sort(s + l,s + mid + 1,cmp1);
sort(s + mid + 1,s + r + 1,cmp1);
int j = l;
for(int i = mid + 1;i <= r;i ++){
while(s[i].id > s[j].id and j <= mid){
add(s[j].t,1);
j ++;
}
ans[s[i].t] += query(s[i].t);
}
for(int i = l;i < j;i ++) add(s[i].t,-1);
sort(s + l,s + mid + 1,cmp2);
sort(s + mid + 1,s + r + 1,cmp2);
j = mid + 1;
for(int i = l;i <= mid;i ++){
while(s[i].id < s[j].id and j <= r){
add(s[j].t,1);
j ++;
}
ans[s[i].t] += query(s[i].t);
}
for(int i = mid + 1;i < j;i ++) add(s[i].t,-1);
}
void work(){
merge(1,n);
CDQ(1,n);
for(int i = 1;i <= m;i ++) printf("%lld\n",num),num -= ans[i];
}
int f[N];
void Input(){
scanf("%lld%lld",&n,&m);
for(int i = 1;i <= n;i ++) scanf("%lld",&s[i].a),s[i].id = i,f[s[i].a] = i;
for(int i = 1,x;i <= m;i ++) scanf("%lld",&x),s[f[x]].t = i;
for(int i = 1,x;i <= n;i ++) if(!s[i].t) s[i].t = m + 1;
}
signed main(){
Input();
work();
return 0;
}
整体二分
整体二分就是多了一个定义域,即相当于求 n 个答案,此时如果一个一个的二分去寻找答案会 TLE,此时我们需要用到整体二分。
过程:
记 \([l,r]\) 为答案的值域,\([L,R]\) 为答案定义域
\((1)\) 分治。每层分治统计答案与 \(mid = l + r >> 1\) 的关系。
\((2)\) 将答案与 \(mid\) 的大小关系分成 \(q1、q2\) 两部分处理(类似归并排序)。
\((3)\) \(l=r\) 时相当于找到答案,记录当前定义域内的答案。
例题:P3527 [POI2011] MET-Meteors
\((1)\) 由于每一个国家的位置是分散的,所以我们可以建一个图,方便从一个国家任意一个点方便到达另一个点进行记录答案,并且记录其对应下标,因为后续排序会打乱顺序,方便后续计算答案。
struct Edge{int next,to;}edge[N];
void add(int from,int to){
edge[++cnt] = (Edge){q[from].h,to};
q[from].h = cnt;
}
void Input(){
n = read(),m = read();
for(int i = 1,a;i <= m;i ++) a = read(),add(a,i);
for(int i = 1;i <= n;i ++) q[i].k = read(),q[i].id = i;
Q = read();
for(int i = 1;i <= Q;i ++) x[i].l = read(),x[i].r = read(),x[i].a = read();
}
\((2)\) 由于它是一个环,所以我们可以对于所有输入中 \(x[i].l > x[i].r\) 的数据的 \(x[i].r\) 加上 \(m\),方面处理,然后在后面统计每一个星球数量的时候可以加上其对应位置 \(y\) 的陨石数量和 \(y+m\) 的陨石数量。
\((3)\) 然后开始分治求解,令 \([l,r]\) 为答案的值域,即本题中的 \([1,k]\),我代码中的 \([1,Q]\),但是本题有无解的情况,所以令值域为 \([1,Q + 1]\),最后答案是 \(Q+1\) 的即为无解的情况;\([L,R]\) 为答案的定义域,即本题中(本代码中)的 \([1,n]\)然后分治求解:
首先,把 \([l,mid]\) 内陨石会降落的数量加到对应的 \([x[i].l,x[i].r]\) 区间内,此时我们用树状数组来维护(此时树状数组相当于一个区间修改,单点查询的树状数组)。
for(int i = l;i <= mid;i ++) Add(x[i].l,x[i].a),Add(x[i].r + 1,-x[i].a);
然后,对于定义域 \([L,R]\) 内所有的国家,利用刚开始建图的方式求解这个国家在此时所获得的陨石数量,记得不光要加上其对应位置 \(edge[j].to\) 的数量,还要加上 \(edge[j].to+m\) 位置的数量。
此时,其现在陨石的数量与其需要的陨石数量 \(q[i].k\) 进行比较,如果大于,证明足够,在区间 \([l,mid]\) 中找最优值;否则,在区间 \([mid + 1,r]\) 中找最优值,并且 \(q[i].k\) 需要减去现在陨石的数量,探后在向右区间找最优值。最后记得清空树状数组。
int lowbit(int x) {return x & (-x);}
void Add(int x,int y) {while(x <= m * 2) c[x] += y,x += lowbit(x);}
int query(int x) {int res = 0;while(x) res += c[x],x -= lowbit(x);return res;}
void solve(int l,int r,int L,int R){
if(l == r){
for(int i = L;i <= R;i ++) ans[q[i].id] = l;
return ;
}
int mid = l + r >> 1,cnt1 = 0,cnt2 = 0;
for(int i = l;i <= mid;i ++) Add(x[i].l,x[i].a),Add(x[i].r + 1,-x[i].a);
for(int i = L;i <= R;i ++){
int tmp = 0;
for(int j = q[i].h;j;j = edge[j].next){
int y = edge[j].to;
tmp += query(y) + query(y + m);
}
if(tmp >= q[i].k) q1[++cnt1] = q[i];
else q[i].k -= tmp,q2[++cnt2] = q[i];
}
for(int i = l;i <= mid;i ++) Add(x[i].l,-x[i].a),Add(x[i].r + 1,x[i].a);
for(int i = 1;i <= cnt1;i ++) q[i + L - 1] = q1[i];
for(int i = 1;i <= cnt2;i ++) q[i + L + cnt1 - 1] = q2[i];
solve(l,mid,L,L + cnt1 - 1);
solve(mid + 1,r,L + cnt1,R);
}
另外需要注意,如果这么算,\(tmp\) 的值在最后一个数据点会爆 long long,一种解决方法是开 __int128,另一种解决方法是在 \(tmp\) 已经大于 \(q[i].k\) 的时候直接跳出循环。
我很感激能够战胜你们,这代表着我的努力正在发挥作用。
#include <bits/stdc++.h>
#define N 300005
#define int __int128
using namespace std;
inline int read(){
int x = 0,f = 1;char ch = getchar();
while(ch < '0' or ch > '9') {if (ch == '-') f = -1;ch = getchar();}
while(ch >= '0' and ch <= '9') x = x * 10 + ch - 48,ch = getchar();
return x * f;
}
inline void write(int x){
if(x < 0) putchar('-'),x = -x;
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
}
struct X{int l,r,a;}x[N];
struct QQ{int k,id,h;}q[N],q1[N],q2[N];
int n,m,Q,c[N << 1],head[N],cnt,ans[N];
struct Edge{int next,to;}edge[N];
void add(int from,int to){
edge[++cnt] = (Edge){q[from].h,to};
q[from].h = cnt;
}
void Input(){
n = read(),m = read();
for(int i = 1,a;i <= m;i ++) a = read(),add(a,i);
for(int i = 1;i <= n;i ++) q[i].k = read(),q[i].id = i;
Q = read();
for(int i = 1;i <= Q;i ++) x[i].l = read(),x[i].r = read(),x[i].a = read();
}
int lowbit(int x) {return x & (-x);}
void Add(int x,int y) {while(x <= m * 2) c[x] += y,x += lowbit(x);}
int query(int x) {int res = 0;while(x) res += c[x],x -= lowbit(x);return res;}
void solve(int l,int r,int L,int R){
if(l == r){
for(int i = L;i <= R;i ++) ans[q[i].id] = l;
return ;
}
int mid = l + r >> 1,cnt1 = 0,cnt2 = 0;
for(int i = l;i <= mid;i ++) Add(x[i].l,x[i].a),Add(x[i].r + 1,-x[i].a);
for(int i = L;i <= R;i ++){
int tmp = 0;
for(int j = q[i].h;j;j = edge[j].next){
int y = edge[j].to;
tmp += query(y) + query(y + m);
}
if(tmp >= q[i].k) q1[++cnt1] = q[i];
else q[i].k -= tmp,q2[++cnt2] = q[i];
}
for(int i = l;i <= mid;i ++) Add(x[i].l,-x[i].a),Add(x[i].r + 1,x[i].a);
for(int i = 1;i <= cnt1;i ++) q[i + L - 1] = q1[i];
for(int i = 1;i <= cnt2;i ++) q[i + L + cnt1 - 1] = q2[i];
solve(l,mid,L,L + cnt1 - 1);
solve(mid + 1,r,L + cnt1,R);
}
void work(){
for(int i = 1;i <= Q;i ++) if(x[i].r < x[i].l) x[i].r += m;
solve(1,Q + 1,1,n);
for(int i = 1;i <= n;i ++){
if(ans[i] == Q + 1) puts("NIE");
else write(ans[i]),puts("");
}
}
signed main(){
Input();
work();
return 0;
}
习题:
\(1.\) P4602 [CTSC2018] 混合果汁
为什么可以用整体二分?因为单个的询问可以用二分去做,因此整体的询问可以使用整体二分。
对于二分答案求解过程中,我们可以利用贪心思想,对于所有美味度优先选择 \(d_i\) 大于 \(mid\) 且 \(p_i\) 较小的果汁。
那么我们可以对于物品按照 \(d_i\) 从大到小排序,然后用线段树维护 \(p_i\),线段树的下标为 \(p_i\),每个节点都保存单价区间内所有物品上限的件数之和以及总价。
每次二分答案时,将所有可选物品(即美味程度小于 \(d_mid\),由于是从大到小排序,所以就相当于 \([1,mid]\) 这个区间里所有的物品)插入线段树,然后通过当前美味程度是否满足定义域内节点将定义域划分成两个区间,分治求解即可。
关于线段树如何修改查询请看代码。
太遗憾了,我能够说服你们留下吗。
#include <bits/stdc++.h>
#define N 100005
#define int long long
using namespace std;
int n,m,ans[N],cur;
struct A{int d,p,l;}a[N];
bool cmp(A a,A b) {return a.d > b.d;}
struct Q{int g,l,id;}q[N],q1[N],q2[N];
void Input(){
scanf("%lld%lld",&n,&m);
for(int i = 1;i <= n;i ++) scanf("%lld%lld%lld",&a[i].d,&a[i].p,&a[i].l);
for(int i = 1;i <= m;i ++) scanf("%lld%lld",&q[i].g,&q[i].l),q[i].id = i;
a[++n] = (A){-1,0,1000000000000000000};sort(a + 1,a + n + 1,cmp);
//这里是插入一个特殊值,方便处理输出 -1 的情况。
}
struct Set_Tree{
struct Tree{int l,r,ans,sum;}t[N << 2];
int ls(int p) {return p << 1;}
int rs(int p) {return p << 1 | 1;}
void build(int p,int l,int r){
t[p].l = l,t[p].r = r,t[p].ans = t[p].sum = 0;
if(l == r) return ;
int mid = l + r >> 1;
build(ls(p),l,mid);
build(rs(p),mid + 1,r);
}
void update(int p,int x,int k,int kk){
if(t[p].l == t[p].r) return (void)(t[p].ans += kk * k,t[p].sum += kk * k * t[p].l);
int mid = t[p].l + t[p].r >> 1;
if(x <= mid) update(ls(p),x,k,kk);
else update(rs(p),x,k,kk);
t[p].ans = t[ls(p)].ans + t[rs(p)].ans;
t[p].sum = t[ls(p)].sum + t[rs(p)].sum;
}
int query(int p,int x){
if(x <= 0) return 0;
if(t[p].l == t[p].r) return x * t[p].l;
int mid = t[p].l + t[p].r >> 1;
if(x <= t[ls(p)].ans) return query(ls(p),x);
else return t[ls(p)].sum + query(rs(p),x - t[ls(p)].ans);
//如果左区间足够,那就在左区间;否则,就去右区间,记得加上左区间的总价,x值对应减去左区间的数量。
}
}Set;
void solve(int l,int r,int L,int R){
if(l == r){
for(int i = L;i <= R;i ++) ans[q[i].id] = a[l].d;
return ;
}
int mid = l + r >> 1,cnt1 = 0,cnt2 = 0;
while(cur < mid) cur ++,Set.update(1,a[cur].p,a[cur].l,1);
while(cur > mid) Set.update(1,a[cur].p,a[cur].l,-1),cur --;
//这样写可以大大降低时间复杂度,避免每次都插入然后全部清空导致 TLE。
for(int i = L;i <= R;i ++){
if(q[i].l > Set.t[1].ans) q2[++cnt2] = q[i];
else if(Set.query(1,q[i].l) <= q[i].g) q1[++cnt1] = q[i];
else q2[++cnt2] = q[i];
}
for(int i = 1;i <= cnt1;i ++) q[i + L - 1] = q1[i];
for(int i = 1;i <= cnt2;i ++) q[i + L + cnt1 - 1] = q2[i];
solve(l,mid,L,L + cnt1 - 1);
solve(mid + 1,r,L + cnt1,R);
}
void work(){
Set.build(1,1,100000);solve(1,n,1,m);
for(int i = 1;i <= m;i ++) printf("%lld\n",ans[i]);
}
signed main(){
Input();
work();
return 0;
}
此博客将会持续更新。

 我的剑不仅只能够杀人,还能够说话哦。
我的剑不仅只能够杀人,还能够说话哦。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号