辛普森积分法小结

近来学了这个知识，似乎没有想象中的那么难。

---

 

问题：

　　  已知$f(x)$, 求定积分$$\int_{L}^{R}f(x)dx$$

 

simpson公式：

　　  设$f(x)\approx g(x)=Ax^2+Bx+C$

　　则有$$\int_{l}^{r}f(x)dx $$$$ \approx \int_{l}^{r}(Ax^2+Bx+C)dx$$$$=\frac{A}{3}(r^3-l^3)+\frac{B}{2}(r^2-l^2)+C(r-l)$$$$=\frac{r-l}{6}(2A(l^2+lr+r^2)+3B(l+r)+6C)$$$$=\frac{r-l}{6}(Al^2+Bl+C+Ar^2+Br+C+4A(\frac{l+r}{2})^2+4B(\frac{l+r}{2})+4C)$$$$=\frac{r-l}{6}(f(l)+f(r)+4f(\frac{l+r}{2}))$$

故：$$\int_{l}^{r}f(x)dx \approx \frac{r-l}{6}(f(l)+f(r)+4f(\frac{l+r}{2}))$$

 

自适应辛普森法：

  　　容易从上面的推导过程发现，辛普森公式是以二次曲线逼近的方式取代矩形或梯形的积分公式。那么如果要求$\int_{L}^{R}f(x)dx$，可以将$[L,R]$分成若干$[l,r]$，但如果$r-l$过大，精度就无法保证；而如果$r-l$过小，时间吃不消。

　　因此有了自适应辛普森法，可以自动控制区间分割的大小，以保证精度。

　　实现就是二分递归的过程，如果$\int_{l}^{mid}f(x)dx+\int_{mid}^{r}f(x)dx$与$\int_{l}^{r}f(x)dx$的差小于需要的精度就结束递归，注意这个精度在递归时也是需要改变的。

　　具体细节看代码。

 

注意事项：

　  　辛普森法其实是一种近似的方法，有可能被刻意针对。下图中三个点在同一二次函数上，这样就会错。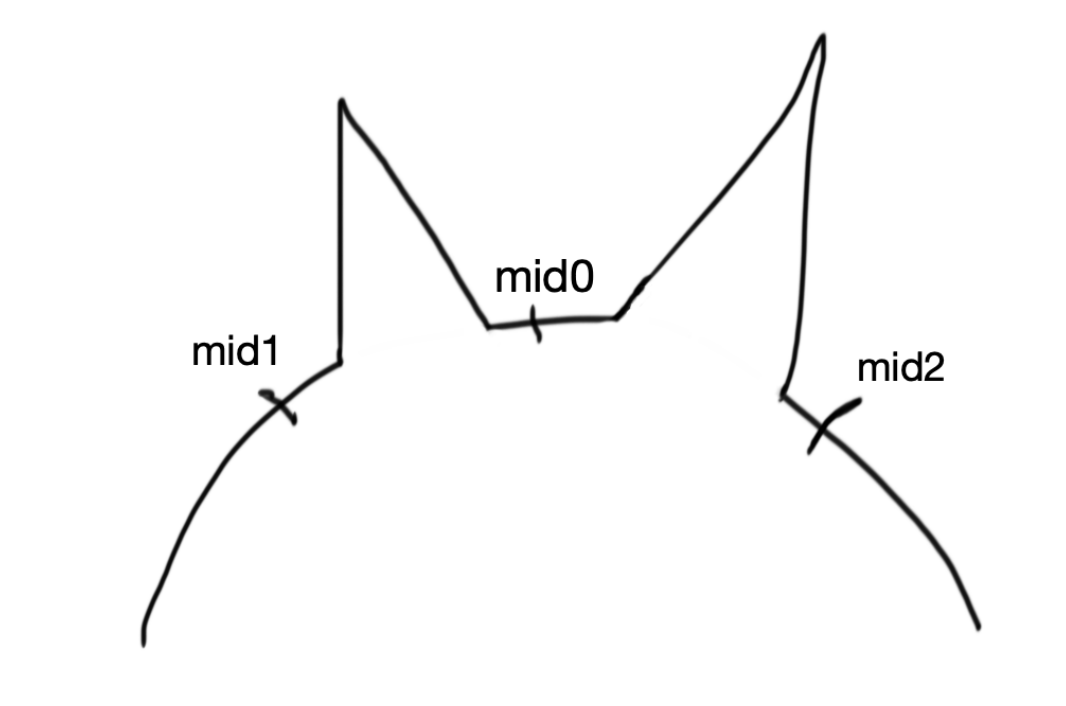

 

 

例题：

　　 [NOI2005]月下柠檬树

解析：

　　 圆的投影还是圆，圆台的侧面投影下去就是底面和顶面投影的切线，围成的图形就是梯形，把圆和梯形表示出来，用辛普森积分法求解即可。

　代码：　

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn = 505;
const double eps = 1e-9;

int n;
double h[maxn];
bool b[maxn];

struct circ{
    double pos, r;
}c[maxn];

struct tpzd{
    double l, r, hl, hr;
}a[maxn];

double calc(double x)
{
    double ret = 0;
    for(int i = 1; i <= n; ++i)
        if(c[i].pos - c[i].r - eps < x && c[i].pos + c[i].r + eps > x)
        {
            ret = max(ret, sqrt(c[i].r * c[i].r - (x - c[i].pos) * (x - c[i].pos)));
        }
    for(int i = 1; i <= n; ++i)
        if(b[i] && a[i].l - eps < x && a[i].r + eps > x)
        {
            ret = max(ret, a[i].hl - (a[i].hl - a[i].hr) * (x - a[i].l) / (a[i].r - a[i].l));
        }
    return ret;
}

double calc2(double l, double r)
{
    double mid = (l + r) / 2;
    return (r - l) * (calc(l) + calc(r) + 4 * calc(mid)) / 6;
}

double solve(double l, double r, double epsn, double las)
{
    double mid = (l + r) / 2, le = calc2(l, mid), ri = calc2(mid, r);
    if(fabs(le + ri - las) < epsn)    return le + ri;
    return solve(l, mid, epsn / 2, le) + solve(mid, r, epsn / 2, ri);
}

int main()
{
    double alp;
    scanf("%d%lf", &n, &alp);
    for(int i = 0; i <= n; ++i)
        scanf("%lf", &h[i]);
    for(int i = 1; i <= n; ++i)
        scanf("%lf", &c[i].r);
    double t = tan(alp), H = 0, L = 0, R = 0, len, tmp;
    for(int i = 1; i <= n + 1; ++i)
    {
        c[i].pos = H / t;
        L = min(L, c[i].pos - c[i].r);
        R = max(R, c[i].pos + c[i].r);
        H += h[i];
    }
    for(int i = 1; i <= n; ++i)
    {
        len = c[i+1].pos - c[i].pos;
        if(fabs(c[i].r - c[i+1].r) > len)    continue;
        b[i] = 1;
        tmp = sqrt(len * len - (c[i].r - c[i+1].r) * (c[i].r - c[i+1].r));
        a[i].l = c[i].pos + c[i].r * (c[i].r - c[i+1].r) / len;
        a[i].r = c[i+1].pos + c[i+1].r * (c[i].r - c[i+1].r) / len;
        a[i].hl = c[i].r * tmp / len;
        a[i].hr = c[i+1].r * tmp / len;
    }
    printf("%.2f", 2 * solve(L, R, 1e-4, calc2(L, R)));
    return 0;
}