【队列】力扣239：滑动窗口最大值

给定一个整数数组和一个滑动窗口大小，求在这个窗口的滑动过程中，每个时刻其包含的最大值。

示例：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置 最大值

---

[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7

输入是一个一维整数数组，和一个表示滑动窗口大小的整数；输出是一个一维整数数组，表示每个时刻时的窗口内最大值。

---

对于每个滑动窗口，可以使用 O(k) 的时间遍历其中的每一个元素，找出其中的最大值。对于长度为 n 的数组 nums 而言，窗口的数量为 n−k+1，因此该算法的时间复杂度为 O((n−k+1)k)=O(nk)，会超出时间限制，因此需要优化。

可以想到，对于两个相邻（只差了一个位置）的滑动窗口，它们共用着 k−1 个元素，而只有 1 个元素是变化的。因此可以根据这个特点进行优化。

优先队列

对于「最大值」，可以想到一种非常合适的数据结构，那就是优先队列（堆），其中的大根堆可以实时维护一系列元素中的最大值。

对于本题而言，初始时，将数组 nums 的前 k 个元素放入优先队列中。每当向右移动窗口时，就可以把一个新的元素放入优先队列中，此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中，在这种情况下，这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此，后续继续向右移动窗口时，这个值就永远不可能出现在滑动窗口中了，可以将其永久地从优先队列中移除。不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系，可以在优先队列中存储二元组 (num, index)，表示元素 num 在数组中的下标为 index。

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        q = [(-nums[i], i) for i in range(k)] # Python 默认的优先队列是小根堆
        heapq.heapify(q)

        ans = [-q[0][0]]
        for i in range(k, n):
            heapq.heappush(q, (-nums[i], i))
            while q[0][1] <= i - k:
                heapq.heappop(q)
            ans.append(-q[0][0])

        return ans

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/sliding-window-maximum/solution/hua-dong-chuang-kou-zui-da-zhi-by-leetco-ki6m/

时间复杂度：O(nlogn)，其中 n 是数组 nums 的长度。在最坏情况下，数组 nums 中的元素单调递增，那么最终优先队列中包含了所有元素，没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O(logn)，因此总时间复杂度为 O(nlogn)。

空间复杂度：O(n)，即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 O(n) 空间，只计算额外的空间使用。

单调队列

可以用双端队列：每当向右移动时，把窗口左端的值从队列左端剔除，把队列右边小于窗口右端的值全部剔除。这样双端队列的最左端永远是当前窗口内的最大值。另外，这道题也是单调栈的一种延伸：该双端队列利用从左到右递减来维持大小关系，因此成为「单调队列」。

思路来源：代码随想录

这里需要一个队列，放进去窗口里的元素，然后随着窗口的移动，队列也一进一出，每次移动之后，队列告诉我们里面的最大值是什么。此外，每次窗口移动的时候，调用 que.pop(滑动窗口中移除元素的数值)，que.push(滑动窗口添加元素的数值)，然后 que.front() 就返回要的最大值。

分析一下，队列里的元素一定是要排序的，而且要最大值放在出队口，要不然怎么知道最大值呢？

但如果把窗口里的元素都放进队列里，窗口移动的时候，队列需要弹出元素。

那么问题来了，已经排序之后的队列怎么能把窗口要移除的元素（这个元素可不一定是最大值）弹出呢？

其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

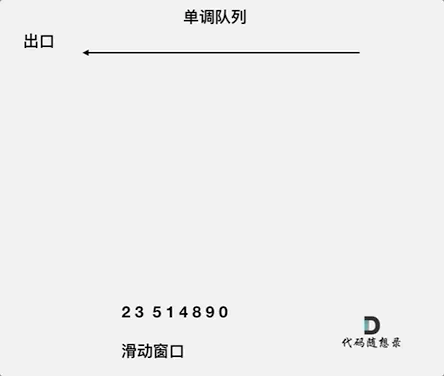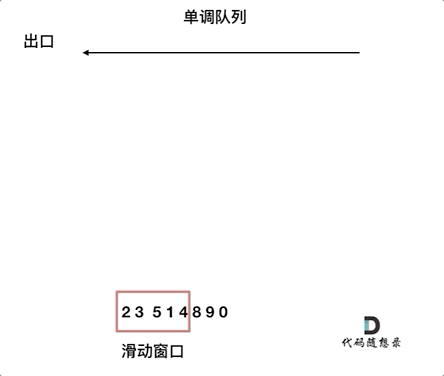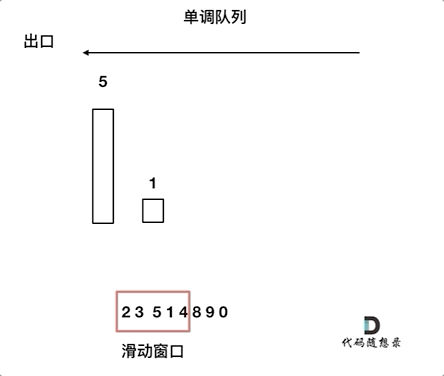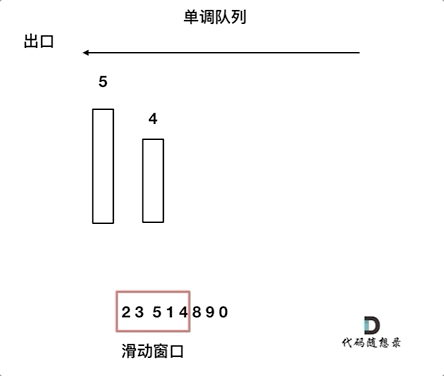
对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。

这个维护元素单调递减的队列就叫做「单调队列」，即单调递减或单调递增的双端队列。这需要自己来构建一个单调队列。

设计单调队列的时候，pop 和 push 操作要保持如下规则：

• pop(value)：如果窗口移除的元素 value 等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
• push(value)：如果 push 的元素 value 大于入口元素的数值，那么就将队列入口的元素弹出，直到 push 元素的数值小于等于队列入口元素的数值为止

保持如上规则，每次窗口移动的时候，只要问 que.front() 就可以返回当前窗口的最大值。

也就是把主动寻找、及时删除的思维转换为被动检测、延迟处理。

确定要使用的数据结构：在没有指定容器的情况下，deque 就是默认底层容器。

理解版：

class MyQueue: # 单调队列（从大到小）
    def __init__(self):
        self.queue = [] #使用list来实现单调队列

    # 每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，如果相等则弹出。
    # 同时 pop 之前判断队列当前是否为空
    def pop(self, value):
        if self.queue and value == self.queue[0]:
            self.queue.pop(0) # list.pop()时间复杂度为O(n)，这里可以使用collections.deque()

    #如果 push 的数值大于入口元素的数值，那么就将队列后端的数值弹出，直到 push 的数值小于等于队列入口元素的数值为止
    #这样就保持了队列里的数值是单调从大到小
    def push(self, value):
        while self.queue and value > self.queue[-1]:
            self.queue.pop()
        self.queue.append(value)

    #查询当前队列里的最大值：直接返回队列前端也就是 front
    def front(self):
        return self.queue[0]

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        que = MyQueue()
        result = []
        for i in range(k): # 先将前 k 的元素放进队列
            que.push(nums[i])
        result.append(que.front()) # result 记录前k的元素的最大值
        for i in range(k, len(nums)):
            que.pop(nums[i - k]) # 滑动窗口移除最前面元素
            que.push(nums[i]) # 滑动窗口前加入最后面的元素
            result.append(que.front()) # 记录对应的最大值
        return result

作者：carlsun-2
链接：https://leetcode.cn/problems/sliding-window-maximum/solution/by-carlsun-2-6b0l/

简洁版：

from collections import deque
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        q = collections.deque()
        for i in range(k):
            while q and nums[i] >= nums[q[-1]]:
                q.pop()
            q.append(i)

        ans = [nums[q[0]]]
        for i in range(k, n):
            while q and nums[i] >= nums[q[-1]]:
                q.pop()
            q.append(i)
            while q[0] <= i - k:
                q.popleft()
            ans.append(nums[q[0]])

        return ans

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/sliding-window-maximum/solution/hua-dong-chuang-kou-zui-da-zhi-by-leetco-ki6m/

时间复杂度：O(n)，其中 n 是数组 nums 的长度。每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)。

空间复杂度：O(k)。与方法一不同的是，这里使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素，因此队列使用的空间为 O(k)。