【搜索】力扣127:单词接龙
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
示例:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
BFS
本题要求的是最短转换序列的长度,看到最短首先想到的就是广度优先搜索。想到广度优先搜索自然而然的就能想到图,但是题目并没有直截了当的给出图的模型,因此我们需要把它抽象成图的模型。
可以把每个单词都抽象为一个结点,如果两个单词可以只改变一个字母进行转换,那么说明它们之间有一条双向边。因此只需要把满足转换条件的结点相连,就形成了一张图
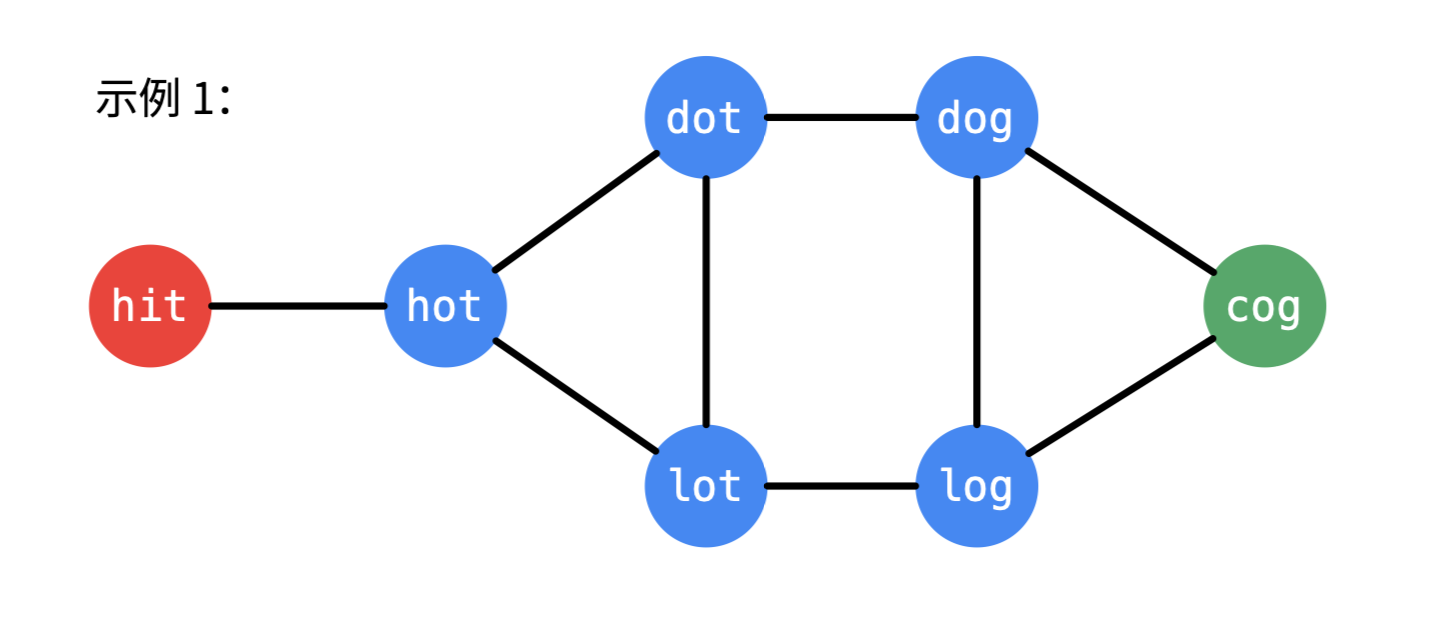
基于该图,以 beginWord 为图的起点,以 endWord 为终点进行广度优先搜索,寻找 beginWord 到 endWord 的最短路径。
实现:
如果一开始就构建图,每一个单词都需要和除它以外的另外的单词进行比较,复杂度是 O(NwordLen),这里 N 是单词列表的长度。
为此,在遍历一开始,把所有的单词列表放进一个哈希表中,然后在遍历的时候构建图,每一次得到在单词列表里可以转换的单词,复杂度是 O(26×wordLen),借助哈希表,找到邻居与 N 无关。
使用 BFS 进行遍历,需要的辅助数据结构:
- 队列
- visited 集合。说明:可以直接在 wordSet (由 wordList 放进集合中得到)里做删除。但更好的做法是新开一个哈希表,遍历过的字符串放进哈希表里。这种做法具有普遍意义。绝大多数在线测评系统和应用场景都不会在意空间开销
from collections import deque
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
# 1. 将 wordList 放到哈希表里,便于判断某个单词是否在 wordList 里
word_set = set(wordList)
if len(word_set) == 0 or endWord not in word_set:
return 0
if beginWord in word_set:
word_set.remove(beginWord)
# 2. 图的广度优先遍历,必须使用队列和表示是否访问过的 visited 哈希表
queue = collections.deque()
queue.append(beginWord)
visited = set(beginWord)
# 3. 开始广度优先遍历,包含起点,因此初始化的时候步数为 1
word_len = len(beginWord)
step = 1
while queue:
current_size = len(queue)
for i in range(current_size):
word = queue.popleft() # 依次遍历当前队列中的单词
word_list = list(word)
for j in range(word_len):
origin_char = word_list[j] # 先保存,后面要恢复
for k in range(26):
word_list[j] = chr(ord('a') + k)
next_word = ''.join(word_list)
if next_word in word_set:
if next_word == endWord: # 如果 currentWord 能够修改 1 个字符与 endWord 相同,则返回 step + 1
return step + 1
if next_word not in visited:
queue.append(next_word)
visited.add(next_word) # 添加到队列以后,必须马上标记为已经访问
word_list[j] = origin_char # 恢复
step += 1
return 0
作者:liweiwei1419
链接:https://leetcode.cn/problems/word-ladder/solution/yan-du-you-xian-bian-li-shuang-xiang-yan-du-you-2/
时间复杂度:O(N×C^2)。其中 N 为 wordList 的长度,C 为列表中单词的长度。
建图过程中,对于每一个单词,需要枚举它连接到的所有虚拟结点,时间复杂度为 O(C),将这些单词加入到哈希表中,时间复杂度为 O(N×C),因此总时间复杂度为 O(N×C)。
广度优先搜索的时间复杂度最坏情况下是 O(N×C)。每一个单词需要拓展出 O(C) 个虚拟结点,因此结点数 O(N×C)。
空间复杂度:O(N×C^2)。哈希表中包含 O(N×C) 个结点,每个结点占用空间 O(C),因此总的空间复杂度为 O(N×C^2)。
双向 BFS
已知目标顶点的情况下,可以分别从起点和目标顶点(终点)执行广度优先遍历,直到遍历的部分有交集,这是双向广度优先遍历的思想。双向BFS可以可观地减少搜索空间大小,从而提高代码运行效率。
更合理的做法是,每次从单词数量小的集合开始扩散。
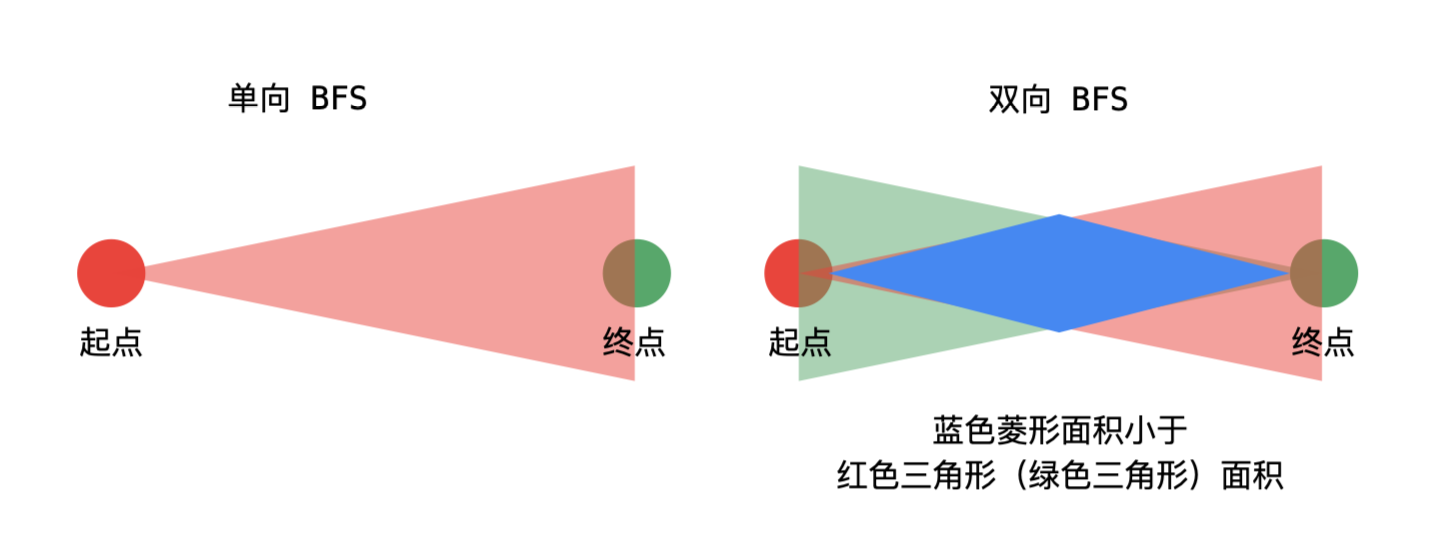
这个题主在BFS部分的具体实现与上一个题主的思路不太相同,更加巧妙,都值得学习。
from collections import deque
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
if endWord not in wordList or not wordList:
return 0
# 1. 将 wordList 放到哈希表里,便于判断某个单词是否在 wordList 里
wordList2Set = set(wordList)
# 2. 图的广度优先遍历
q1 = collections.deque([beginWord])
q2 = collections.deque([endWord])
visited = set([beginWord, endWord]) # 标记数组形式变化
# 3. 开始广度优先遍历,执行双向 BFS。转换序列包含起点,因此初始化的时候步数为 1
step = 1
while q1 and q2:
if len(q1) > len(q2): # 保证每次搜索从长度小的那一端开始,这样考虑到的情况更少
q1, q2 = q2, q1
for _ in range(len(q1)):
cur_word = q1.popleft() # 依次遍历当前队列中的单词
for i in range(len(cur_word)):
for j in range(26):
tmp = cur_word[:i] + chr(ord('a') + j) + cur_word[i + 1:] # 修改位置 i 上的字符
if tmp in wordList2Set:
if tmp in q2: # 如果修改后的单词 tmp 与 endWord 相同,则返回 step + 1
return step + 1
if tmp not in visited:
q1.append(tmp)
visited.add(tmp) # 添加到队列以后,必须马上标记为已经访问
step += 1
return 0
作者:frostep
链接:https://leetcode.cn/problems/word-ladder/solution/python3bfsde-si-lu-you-hua-guo-cheng-700-4fkp/
时间复杂度:O(N×C^2)。其中 N 为 wordList 的长度,C 为列表中单词的长度。
双向广度优先搜索的时间复杂度最坏情况下是 O(N×C)。每一个单词需要拓展出 O(C) 个虚拟结点,因此节点数 O(N×C)。
空间复杂度:O(N×C^2)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号