【回溯】力扣51：N 皇后（太难了）

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例：

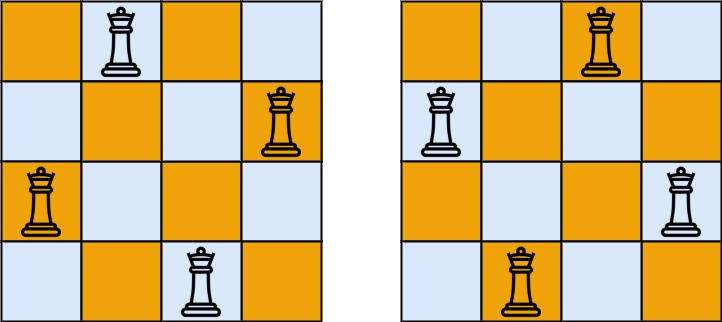
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],// Solution 1
["..Q.","Q...","...Q",".Q.."] // Solution 2 ]
解释：如上图所示，4 皇后问题存在两个不同的解法。

---

回溯法

类似于在矩阵中寻找字符串，本题也是通过修改状态矩阵来进行回溯。不同的是，需要对每一行、列、左斜、右斜建立访问数组，来记录它们是否存在皇后。

本题有一个隐藏的条件，即满足条件的结果中每一行或列有且仅有一个皇后。这是因为一共只有 n 行和 n 列。所以如果通过对每一行遍历来插入皇后，就不需要对行建立访问数组了。

回溯的具体做法是：使用一个数组记录每行放置的皇后的列下标，依次在每一行放置一个皇后。每次新放置的皇后都不能和已经放置的皇后之间有攻击：即新放置的皇后不能和任何一个已经放置的皇后在同一列以及同一条斜线上，并更新数组中的当前行的皇后列下标。当 N 个皇后都放置完毕，则找到一个可能的解。当找到一个可能的解之后，将数组转换成表示棋盘状态的列表，并将该棋盘状态的列表加入返回列表。

由于每个皇后必须位于不同列，因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有 N 列可以选择，第二个皇后最多有 N-1 列可以选择，第三个皇后最多有 N-2 列可以选择（如果考虑到不能在同一条斜线上，可能的选择数量更少），因此所有可能的情况不会超过 N! 种，遍历这些情况的时间复杂度是 O(N!)。

为了降低总时间复杂度，每次放置皇后时需要快速判断每个位置是否可以放置皇后，显然，最理想的情况是在 O(1) 的时间内判断该位置所在的列和两条斜线上是否已经有皇后。

1. 因为是二维矩阵，需要 横纵[x, y] 来标记位置，但一行只能出现一个皇后，可以使用一个长度为 n 的数组 queen 来表示每个皇后的纵坐标 (对应索引就是横坐标)。 假设 n 为 4 ，第一个皇后可以选 4 个位置， 第二个只能选 剩余3个，2个，1个…… 以此类推。

2. 对角线不冲突需要做的是：通过两个集合 diagonal1， diagonal2表示主对角线, 侧对角线。根据规律分别是在一条对角线的 1. row - col 相等 和 2. row + col 相等，来判断当前元素对角线是否已有元素。

3. 找到符合条件的 "纵坐标列表"之后拼接出答案，添加进结果集 res。

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        # 定义所需变量
        res = [] # 结果集
        diagonal1, diagonal2 = set(), set() # 斜对角线
        col = set() # 每一列不能重复
        queen = [-1] * n # 表示皇后位置的数组
        row = ["."] * n # 定义一个长度为 n 元素全为"."的数组，用于最后根据皇后位置输出结果

        def getNQueens(queen_row: int):
            # 5. 如果长度满足 n，就构造结果，加入到结果集 res 中
            if queen_row == n: # queen_row 表示二维矩阵的每一行。因为每一行要选择一个位置放置一个皇后
                ans = list()
                for i in range(n):
                    row[queen[i]] = "Q"
                    ans.append("".join(row))
                    row[queen[i]] = "." # 把更改变回来，下次遍历使用
                res.append(ans)

            for i in range(n):
                # 1. 横，纵，对角线冲突，剪枝
                if i in col or queen_row - i in diagonal1 or queen_row + i in diagonal2:
                    continue
                # 2. 维护状态信息
                diagonal1.add(queen_row - i)
                diagonal2.add(queen_row + i)
                col.add(i)
                queen[queen_row] = i
                # 3. 递归执行下一行
                getNQueens(queen_row + 1)
                # 4. 回溯，去掉状态的更改
                diagonal1.remove(queen_row - i)
                diagonal2.remove(queen_row + i)
                col.remove(i)
                # 可加可不加，这位置是否有值是 col 确定的，回溯 col 即可
                queen[queen_row] = -1

        getNQueens(0) # 调用函数
        return res

作者：1501615430
链接：https://leetcode.cn/problems/n-queens/solution/36-ms-zai-suo-you-python3-ti-jiao-zhong-7o4pb/

一个字典搞定

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        if n == 1:
            return [["Q"]]
        if n == 0:
            return

        d = dict() # 用字典标记。d[row] = col
        res = []

        def addBoard(): # 添加新棋盘
            board = []
            for i in range(n):
                s = "." * d[i] + "Q" + "." * (n - d[i] - 1)
                board.append(s)
            res.append(board)

        def backtrack(i: int) -> int:
            if i == n:
                addBoard()
            for j in range(n):
                if j in d.values():
                    continue
                if all(i - ii != abs(j - d[ii]) for ii in d.keys()): # 判断是否位于对角线
                    d[i] = j
                    backtrack(i + 1)
                    d.pop(i)

        backtrack(0)
        return res

作者：lincs
链接：https://leetcode.cn/problems/n-queens/solution/python3-shi-yong-dan-ge-zi-dian-dictji-k-g0y5/

时间差了点