【回溯】力扣77:组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。可以按 任何顺序 返回答案。
示例:
输入:n = 4, k = 2
输出:[[2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]
回溯法
排列回溯的是交换的位置,而组合回溯的是否把当前的数字加入结果中。
直接的解法当然是使用 for 循环,k 为几就有几层循环。例如示例中 k 为 2,很容易想到用两个 for 循环,这样就可以输出和示例中一样的结果。
int n = 4;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
cout << i << " " << j << endl;
}
}
作者:carlsun-2
链接:https://leetcode.cn/problems/combinations/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-hui-s-0uql/
但是一旦 k 的值较大,用 for 循环嵌套连暴力都写不出来。
那么就可以用回溯法+递归来解决嵌套层数的问题。每一次的递归中嵌套一个for循环,那么递归就可以用于解决多层嵌套循环的问题了。
把组合问题抽象为如下树形结构:
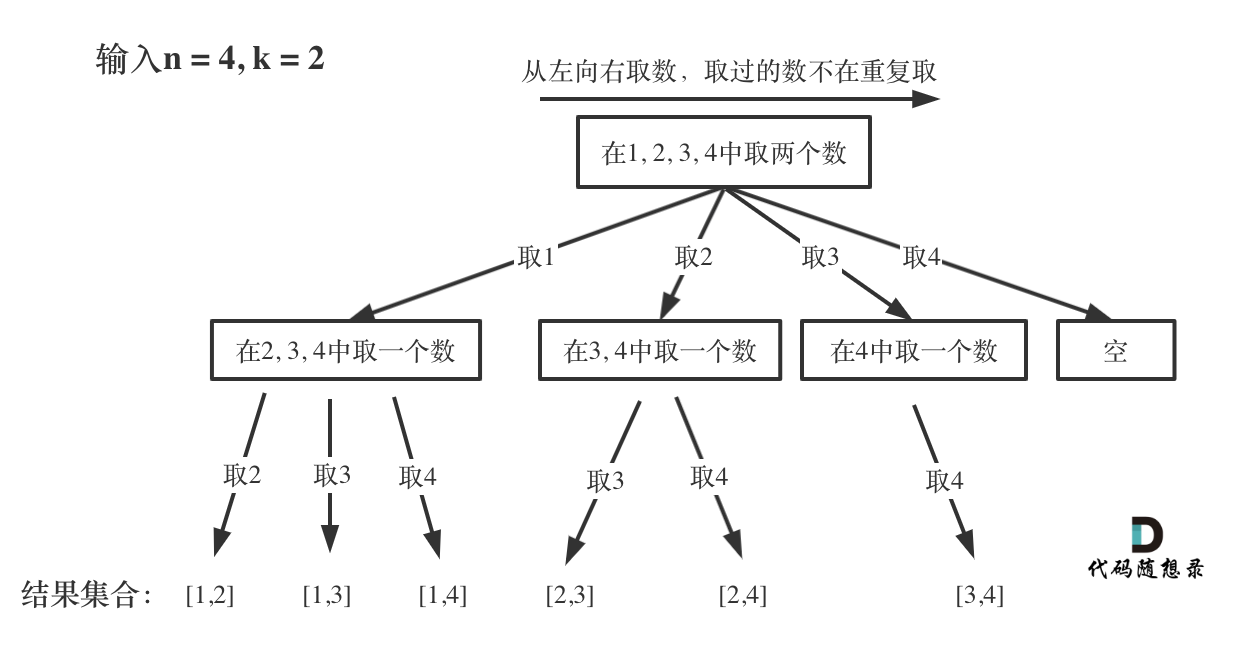
- 从左向右取数,取过的数不再重复取
- 每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围
- n 相当于树的宽度,k 相当于树的深度
- 每次搜索到了叶子结点,就找到了一个结果。只需要把达到叶子结点的结果收集起来,就可以求得 n 个数中 k 个数的组合集合
三步骤
1. 递归函数的返回值以及参数
-
定义两个全局变量
-
res 结果集
-
path 用来存放符合条件单一结果,也就是结果集中的一个数组
其实不定义这两个全局变量也是可以的,可以把这两个变量放进递归函数的参数里。但函数里参数太多影响可读性。
-
递归函数里一定有两个参数,既然是集合 n 里面取 k 个数,那么 n 和 k 是两个int型的参数
-
定义一个参数,int型变量startIndex,用来记录本层递归中,集合从哪里开始遍历(集合就是[1,...,n] )。每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠 startIndex
for i in range(startIndex, n + 1)
-
2. 回溯函数终止条件
path 这个数组的大小如果达到 k,说明找到了一个子集大小为 k 的组合了,此时用二维数组 res 保存这个 path,并终止本层递归。
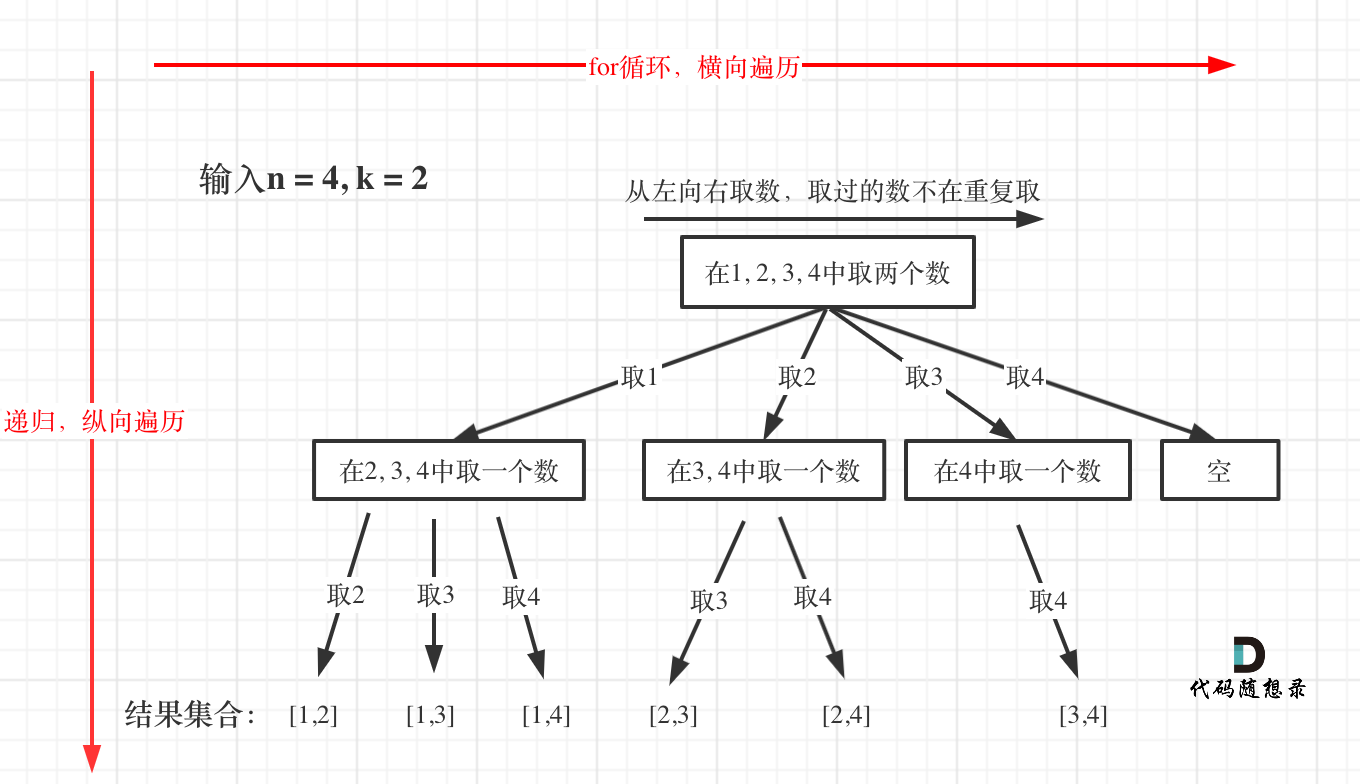
3. 单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,for 循环用来横向遍历,递归的过程是纵向遍历,最后回溯撤销
-
for 循环每次从 startIndex 开始遍历,用 path 保存取到的结点 i
-
backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子结点,遇到了叶子结点就返回
代码
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = [] # 存放符合条件结果的集合
path = [] # 用来存放符合条件结果
def backtrack(n, k, StartIndex):
if len(path) == k:
res.append(path[:])
return
for i in range(StartIndex, n - (k - len(path)) + 2):
path.append(i) # 处理结点
backtrack(n, k, i + 1) # 递归
path.pop() # 回溯,撤销处理的结点
backtrack(n, k, 1)
return res
作者:carlsun-2
链接:https://leetcode.cn/problems/combinations/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-hui-s-0uql/
4. 回溯 + 剪枝
如果 n = 4,k = 4 的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
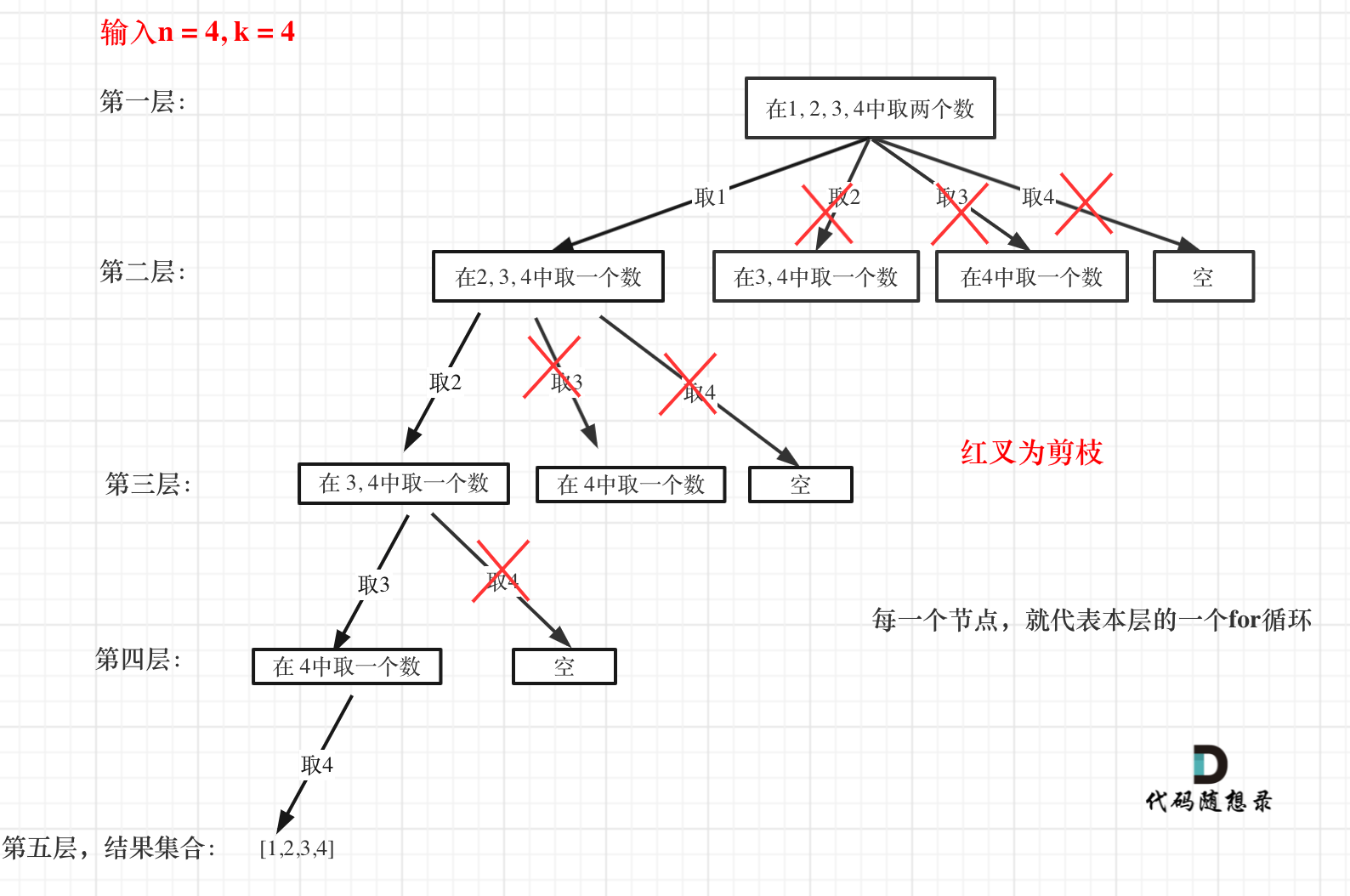
图中每一个结点就代表本层的一个 for 循环,那么每一层的 for 循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
所以,可以剪枝的地方就在递归中每一层的 for 循环所选择的起始位置。
如果 for 循环选择的起始位置之后的元素个数已经不足所需要的元素个数了,那么就没有必要搜索了。
for i in range(startIndex, n - (k - path.size()) + 2) # i为本次搜索的起始位置
其中:path.size() 为已经选择的元素个数,k - path.size() 为还需要的元素个数。因此中至多要从该起始位置 n - (k - path.size()) + 1 开始遍历。range()函数左闭右开,所以还要加 1。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
path = []
def backtrack(n, k, startIndex):
if len(path) == k:
res.append(path[:])
return
for i in range(startIndex, n - (k - len(path)) + 2): # 优化处:剪枝
path.append(i)
backtrack(n, k, i + 1)
path.pop()
backtrack(n, k, 1)
return res
作者:carlsun-2
链接:https://leetcode.cn/problems/combinations/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-hui-s-0uql/
可以发现,需要传入递归函数的参数其实只有 startIndex、path、k - len(path),k - len(path) 就是回溯树的深度 depth
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
def dfs(startIndex, path, depth):
if depth == 0:
res.append(path[:])
else:
for i in range(startIndex, n + 2 - depth):
path.append(i)
dfs(i + 1, path, depth - 1)
path.pop()
dfs(1, [], k) # 这里定义了 path = []
return res
公式法
数学中的组合公式为 C(n, k) = C(n - 1, k) + C(n - 1, k - 1)。
在 [1, n] 中选 k 个数,那么按照字典序可以在 [1, n - k + 1] 中选一个数 i ,然后在 [i + 1, n] 中选出其余 (k - 1) 个数,通过递归进行搜索即可。
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
def merge(array, k):
if k == 1: # 特殊情形
return [[i] for i in array]
else:
res = [] # 结果集
for i in range(n - k + 1): # 选出数 i。注意:[1, n - k + 1] 的索引就是 [0, n - k + 1)
curr = merge(array[i + 1:], k - 1) # 构造在数 x 后面的数组
for j in curr: # 选出其余 k-1 个数
res.append([array[i]] + j)
return res
return merge(list(range(1, n + 1)), k) # 数组 array 就是[1, ..., n]
思路简单,但是容易超出时间限制


 浙公网安备 33010602011771号
浙公网安备 33010602011771号