【搜索】力扣417：太平洋大西洋水流问题

给定一个二维的非负整数矩阵，每个位置的值表示海拔高度。假设左边和上边是太平洋，右边和下边是大西洋，求从哪些位置向下流水，可以同时流到太平洋和大西洋。水只能从海拔高的位置流到海拔低或相同的位置。

示例：

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

输入是一个二维的非负整数数组，表示海拔高度。输出是一个二维的数组，其中第二个数组的维度大小固定为 2，表示满足条件的位置坐标。

参考：
【负雪明烛】反向思考，算法图解

虽然题目要求的是满足向下流能到达两个大洋的位置，如果对所有的位置进行搜索，那么在不剪枝的情况下复杂度会很高。因此可以反过来想，从两个大洋分别开始向上流，这样只需要对矩形四条边进行搜索，分别用 p_visited 和 a_visited 表示能到达的位置。搜索完成后，只需遍历一遍矩阵，满足条件的位置即为两个大洋向上流都能到达的位置。

从太平洋边上的结点出发：

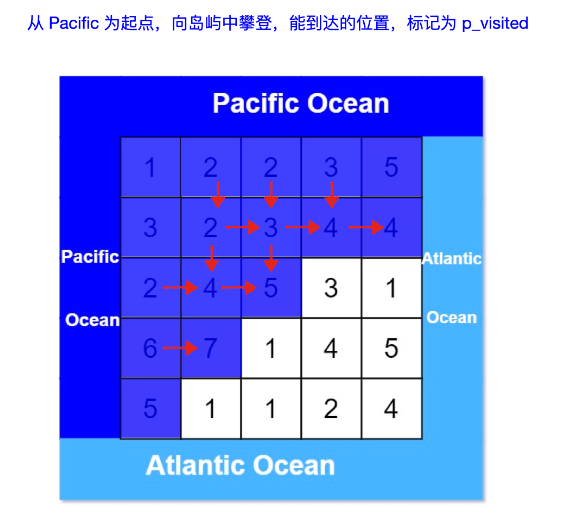
从大西洋边上的结点出发：

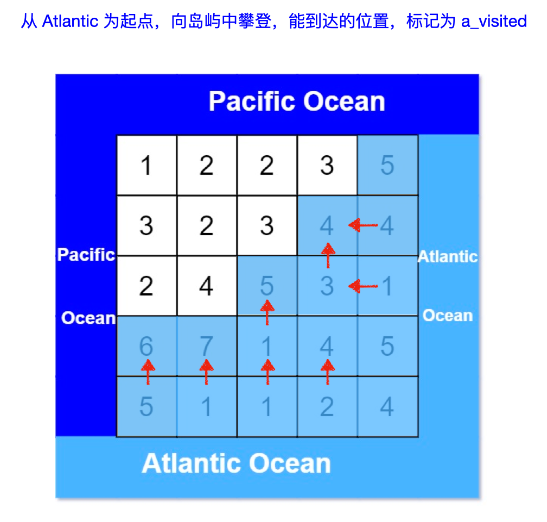
p_visited 和 a_visited 的交集即为所求：

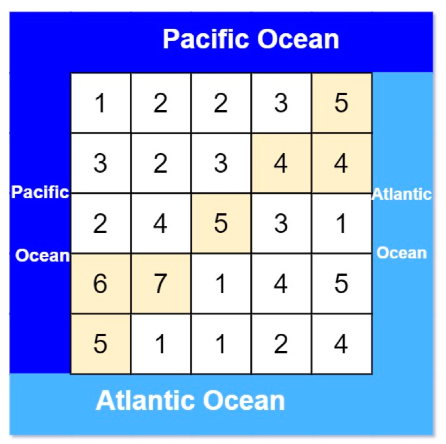
深度优先搜索

• 一般来说 DFS 需要有固定的起点，但是对于本题，四条边都是能与大洋接壤的，那么就把四条边界的每个位置都算作 DFS 的起点

• 使用两个二维数组 p_visited 和 a_visited，分别记录水往“高处”流所能到达的位置

• 对四条边进行遍历，以这些边的每个结点为起点向“高处”流；把能到达的那些的位置，分别在数组 p_visited 和 a_visited 标记出来

class Solution:
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        if not heights:
            return []
        m, n = len(heights), len(heights[0])
        res = []
        p_visited, a_visited = [[False] * n for _ in range(m)], [[False] * n for _ in range(m)] # 两个记录矩阵的初始化其实是一样的
        # 搜索左右两边的结点
        for i in range(m):
            self.dfs(p_visited, heights, m, n, i, 0) # 搜索左边Pacific岸，此时 j == 0
            self.dfs(a_visited, heights, m, n, i, n - 1) # 搜索右边Atlantic岸，此时 j == n-1
        # 搜索上下两边的结点
        for j in range(n):
            self.dfs(p_visited, heights, m, n, 0, j) # 搜索上边Pacific岸，此时i == 0
            self.dfs(a_visited, heights, m, n, m - 1, j) # 搜索下边Atlantic岸，此时 i == m-1
        # 求交集：均为True即加入结果集
        for i in range(m):
            for j in range(n):
                if p_visited[i][j] and a_visited[i][j]:
                    res.append([i, j]) # 加入结果集的是满足条件的结点的坐标
        return res

    def dfs(self, visited, heights, m, n, i, j):
        visited[i][j] = True
        directions = [(-1,0), (1,0), (0,-1), (0,1)] # 建立移动坐标
        for dir in directions:
            x, y = i + dir[0], j + dir[1]
            if not 0 <= x < m or not 0 <= y < n or visited[x][y] or heights[x][y] < heights[i][j]:
                continue
            self.dfs(visited, heights, m, n, x, y)

时间复杂度：O(mn)，其中 m 和 n 分别是矩阵 heights 的行数和列数。最多遍历每个单元格两次，寻找太平洋和大西洋都可以到达的单元格需要遍历整个矩阵，因此时间复杂度是 O(mn)。

空间复杂度：O(mn)。深度优先搜索的递归调用层数是 O(mn)，记录每个单元格是否可以到达太平洋和大西洋需要 O(mn) 的空间，因此空间复杂度是 O(mn)。

广度优先搜索

搜索过程中，同样需要记录每个单元格是否可以从太平洋反向到达，以及是否可以从大西洋反向到达。

反向搜索结束之后，遍历每个网格，如果一个网格既可以从太平洋反向到达也可以从大西洋反向到达，则该网格满足太平洋和大西洋都可以到达，将该网格添加到答案中。

class Solution:
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        m, n = len(heights), len(heights[0])

        def bfs(starts: List[Tuple[int, int]]) -> Set[Tuple[int, int]]:
            q = deque(starts)
            visited = set(starts)
            while q:
                x, y = q.popleft()
                for nx, ny in ((x, y + 1), (x, y - 1), (x - 1, y), (x + 1, y)):
                    if 0 <= nx < m and 0 <= ny < n and heights[nx][ny] >= heights[x][y] and (nx, ny) not in visited:
                        q.append((nx, ny))
                        visited.add((nx, ny))
            return visited

        pacific = [(0, i) for i in range(n)] + [(i, 0) for i in range(1, m)]
        atlantic = [(m - 1, i) for i in range(n)] + [(i, n - 1) for i in range(m - 1)]
        return list(map(list, bfs(pacific) & bfs(atlantic)))

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/pacific-atlantic-water-flow/solution/tai-ping-yang-da-xi-yang-shui-liu-wen-ti-sjk3/

时间复杂度：O(mn)。
空间复杂度：O(mn)。广度优先搜索的队列空间是 O(mn)，记录每个单元格是否可以到达太平洋和大西洋需要 O(mn) 的空间，因此空间复杂度是 O(mn)。