【复杂数据结构】力扣146：LRU 缓存 - 哈希表和双向链表

请你设计并实现一个满足 LRU(最近最少使用)缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity)：以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key)：如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1
void put(int key, int value)：
- 如果关键字 key 已经存在，则变更其数据值 value
- 如果关键字 key 不存在，则向缓存中插入该组 key-value
- 如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {2=2, 1=1}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {3=3, 1=1}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4

说人话：

每次将信息插入未满的缓存的时候，以及更新或查找一个缓存内存在的信息的时候，将该信息标为最近使用
在缓存满的情况下将一个新信息插入的时候，移除最旧的信息，插入新信息，并将该信息标为最近使用

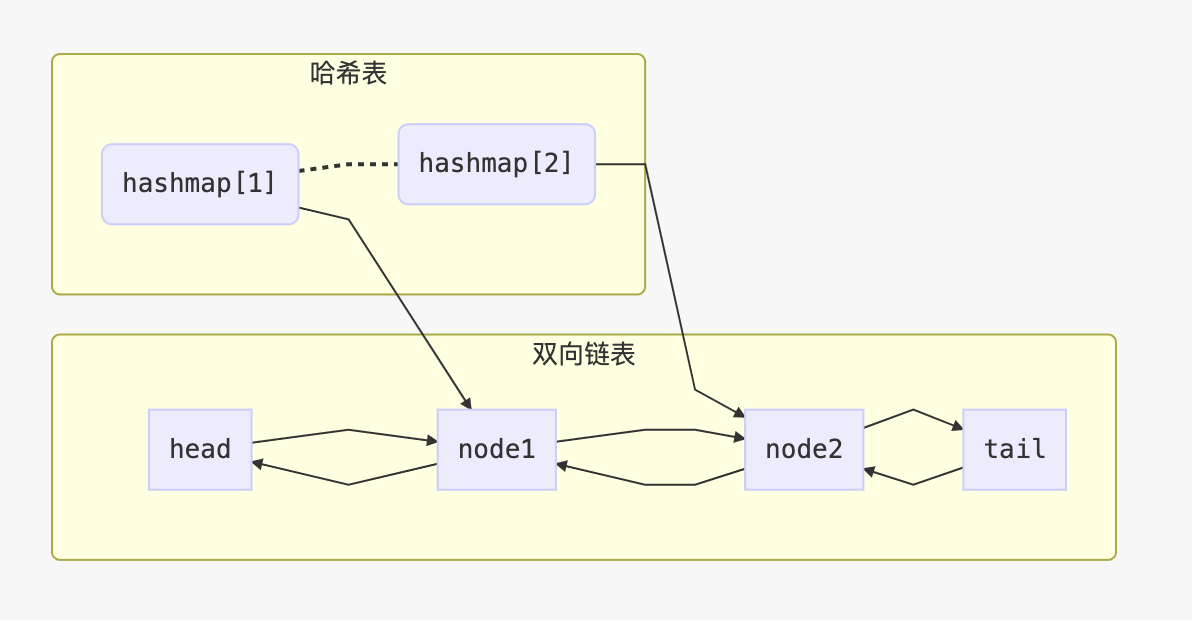
哈希表 + 双向链表

由 key-value 形式的数据结构想到哈希表，由时间复杂度及更新原则想到双向链表：

双向链表按照被使用的顺序存储了这些键值对，靠近头部的键值对是最近使用的，而靠近尾部的键值对是最久未使用的，可以在 O(1) 时间内支持如下操作：
- 撤出队列中某一项removeNode
- 将队列中某一项加到头部addToHead
- 删除最末尾一项removeTail
- 将结点移到尾部需要从头遍历到该结点才能保证链表不断，对于这种情况需要的时间复杂度是 O(n)，用队列实现也不必说，是 O(n)
哈希表通过缓存数据的键映射到其在双向链表中的位置

因此，先使用哈希表进行定位，找出缓存项在双向链表中的位置，随后将其移动到双向链表的头部，即可在 O(1) 的时间内完成 get 或 put 操作：

对于 get 操作，首先判断 key 是否存在：
- 如果 key 不存在，返回 −1
- 如果 key 存在，key 对应的结点是最近被使用的结点
  - 通过哈希表定位到该结点在双向链表中的位置，并将其移动到双向链表的头部
  - 最后返回该结点的值
对于 put 操作，首先判断 key 是否存在：
如果 key 不存在
- 使用 key 和 value 创建一个新的结点，在双向链表的头部添加该结点，并将 key 和该结点添加进哈希表中
- 然后判断双向链表的结点数是否超出容量，如果超出容量，则删除双向链表的尾部结点，并删除哈希表中对应的项
如果 key 存在，则与 get 操作类似。先通过哈希表定位，再将对应的结点的值更新为 value，并将该结点移到双向链表的头部

上述各项操作中，访问哈希表的时间复杂度为 O(1)，在双向链表的头部添加结点、在双向链表的尾部删除结点的复杂度也为 O(1)。而将一个结点移到双向链表的头部，可以分成「删除该结点」和「在双向链表的头部添加结点」两步操作，都可以在 O(1) 时间内完成。

另外要注意的是，在双向链表的实现中，使用一个伪头部（dummy head）和伪尾部（dummy tail）标记界限，这样在添加结点和删除结点的时候就不需要检查相邻的结点是否存在。

class ListNode:
    def __init__(self, key = 0, value = 0):
        self.key = key
        self.value = value
        # 双向链表移动除头尾外的每个结点都需要对结点前后的两个结点进行操作
        self.prev = None
        self.next = None

class LRUCache:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.hashmap = {} # dict()
        # 新建伪头部和伪尾部结点
        self.head = ListNode()
        self.tail = ListNode()
        # 初始化链表为 head <-> tail
        self.head.next = self.tail
        self.tail.prev = self.head
        self.size = 0

    def get(self, key: int) -> int:
        if key not in self.hashmap:
            return -1
        # else的情况（key存在）：先通过哈希表定位，再移动到头部，最后返回值
        node = self.hashmap[key]
        self.removeNode(node)
        self.addToHead(node)
        return node.value

    def put(self, key: int, value: int) -> None:
        # 如果关键字 key 不存在，创建一个新结点，并添加到哈希表
        if key not in self.hashmap:
            node = ListNode(key, value)
            self.hashmap[key] = node
            self.addToHead(node)
            self.size += 1
            # 如果加入新结点后超出容量，删除最后一个结点，并删除哈希表中对应的项
            if self.size > self.capacity: # len(self.hashmap) == self.capacity
                removed = self.removeTail()
                self.hashmap.pop(removed.key)
                self.size -= 1
        # 如果关键字 key 存在，先通过哈希表定位，再修改 value，并移动到头部
        else:
            node = self.hashmap[key]
            node.value = value # 新put的值
            self.removeNode(node)
            self.addToHead(node)

    # get和put操作都可能需要将双向链表中的某个结点移到头部，表示最近访问的结点，所以需要定义新方法：先撤出结点，再添加到头部
    def removeNode(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev
    def addToHead(self, node):
        # 变 node 的前后指向
        node.prev,node.next = self.head, self.head.next
        # 变指向 node 的连接，注意顺序，反了会断链
        self.head.next.prev = node
        self.head.next = node

    # put操作可能需要将双向链表中的末尾结点移除（超出容量capacity）
    def removeTail(self):
        # 定位
        node = self.tail.prev # 末尾结点是伪尾部结点的前一个结点
        # 撤出
        self.removeNode(node)
        return node


# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

时间复杂度：对于 put 和 get 都是 O(1)。

空间复杂度：O(capacity)，因为哈希表和双向链表最多存储 capacity + 1 个元素。

附：利用已封装数据结构（了解即可）

实现本题的两种操作，需要用到一个哈希表和一个双向链表。在面试中，面试官一般会期望面试者能够自己实现一个简单的双向链表，而不是使用语言自带的、封装好的数据结构。在 Python 语言中，有一种结合了哈希表与双向链表的数据结构 OrderedDict，只需要短短的几行代码就可以完成本题。在 Java 语言中，同样有类似的数据结构 LinkedHashMap。这些做法都不会符合面试官的要求。

from collections import OrderedDict
class LRUCache:

    def __init__(self, capacity: int):
        super().__init__() # super() 调用父类(超类)，super().__init__() 既继承类中表层的方法和表层属性，也继承方法内部的属性
        self.capacity = capacity

    def get(self, key: int) -> int:
        if key not in self:
            return -1
        self.move_to_end(key)
        return self[key]

    def put(self, key: int, value: int) -> None:
        if key in self:
            self.move_to_end(key)
        self[key] = value
        if len(self) > self.capacity:
            self.popitem(last=False)

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/lru-cache/solution/lruhuan-cun-ji-zhi-by-leetcode-solution/

posted @ 2022-07-29 11:28 Vonos 阅读(139) 评论(0) 收藏举报

刷新页面返回顶部

Jojo-L

【复杂数据结构】力扣146：LRU 缓存 - 哈希表和双向链表

哈希表 + 双向链表

附：利用已封装数据结构（了解即可）

公告