【图】力扣785:判断二分图(待更并查集)
存在一个 无向图 ,图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,对于 graph[u] 中的每个 v ,都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性:
不存在自环(graph[u] 不包含 u)。
不存在平行边(graph[u] 不包含重复值)。
如果 v 在 graph[u] 内,那么 u 也应该在 graph[v] 内(该图是无向图)
这个图可能不是连通图,也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
如果图是二分图,返回 true ;否则,返回 false 。
示例1:
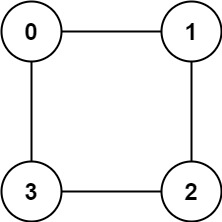
输入:graph = [[1,3],[0,2],[1,3],[0,2]]。输入是邻接链表表示的图(如位置 0 的邻接链表为 [1,3],表示 0 与 1、 0 与 3 相连)
输出:true
解释:可以将节点分成两组: {0, 2} 和
示例2:
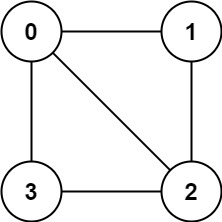
输入:graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出:false
解释:不能将节点分割成两个独立的子集,以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。
基础知识
- 二分图
若无向图 G = (V, E) 的顶点集 V 可以分割为两个互不相交的子集,且图中每条边的两个顶点分别属于不同的子集,则称图 G 为一个二分图。
- 二分图算法
二分图算法也称为染色法,是一种广度优先搜索。如果可以用两种颜色对图中的节点进行着色,并且保证相邻的节点颜色不同,那么图为二分。
算法流程:
-
所有结点均为无色(0)
-
任选一个结点开始,将其染成红色(1),并从该结点开始对整个无向图进行遍历
-
在遍历的过程中,如果通过结点 u 遍历到了结点 v(即 u 和 v 在图中有一条边直接相连),那么有两种情况:
-
如果 v 未被染色,就将其染成与 u 不同的颜色如绿色(-1),并对 v 直接相连的结点进行遍历
-
如果 v 被染色,并且颜色与 u 相同,说明给定的无向图不是二分图。可以直接退出遍历并返回 false
-
-
遍历顺利结束则说明给定的无向图是二分图,返回 true。
注意:题目给定的无向图不一定保证连通,因此需要进行多次遍历,直到每一个结点都被染色,或确定答案为 false 为止。
深度优先搜索 DFS
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph) # 点的个数
if n == 0:
return True
colors = [0] * n # 染色数组,所有元素初始化为 0。colors[i] 标记结点 i 的状态,0 为未着色,1 为着红色,-1 为着绿色
red, green = 1, -1 # 不可以不规定 red,因为调用 dfs 时需要用到
def dfs(node, color):
colors[node] = color # 给当前结点着色
color_neighber = -color # color_neighber = green if color == red else red,因为设置的颜色代数为相反数,所以可以巧妙地用负号而不是判断语句
for neighber in graph[node]: # 遍历结点所在的连通图
if colors[neighber] == 0: # 没有染色就给染相反色
colors[neighber] = color_neighber
if not dfs(neighber, color_neighber):
return False
elif colors[neighber] == color_neighber: # 染色合规则跳过,不需重复着色
continue
else: # 染色矛盾,返回false
return False
return True
for i in range(n): # 遍历每一个结点,也就是给其连通图染色
if colors[i] == 0: # 如果该结点未被染色,启动搜索对该连通图进行染色
if not dfs(i, red): # 给第一个结点染上红色
return False
return True
也可以用一个 flag 变量来记录布尔值:
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
red, green = 1, 2
color = [0] * n
valid = True
def dfs(node: int, color: int):
nonlocal valid # 声明之后的变量既不是全局变量,也不是局部变量,只在调用的子函数中发挥作用
color[node] = color
color_neighber = - color
for neighbor in graph[node]:
if color[neighbor] == 0:
dfs(neighbor, color_neighber)
if not valid:
return
elif color[neighbor] != color_neighber: # else 就是合规的情况,此时不需要再写,因为 valid 默认是true
valid = False
return
for i in range(n):
if color[i] == 0:
dfs(i, red)
if not valid:
break
return valid
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/is-graph-bipartite/solution/pan-duan-er-fen-tu-by-leetcode-solution/
时间复杂度:O(n+m),其中 n 和 m 分别是无向图中的点数和边数。
空间复杂度:O(n),存储结点颜色的数组需要O(n) 的空间,并且在深度优先搜索的过程中,栈的深度最大为 n,需要 O(n) 的空间。
广度优先搜索 BFS
新建队列queue
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
if n == 0:
return True
colors = [0] * n
red, green = 1, -1
def bfs(node, color):
queue = [[node, color]]
while queue:
node, color = queue.pop(0) # 给当前结点着色
color_neighber = -color # 给邻接结点着色
for neighber in graph[node]:
if colors[neighber] == 0: # 没有染色
colors[neighber] = color_neighber
queue.append([neighber, color_neighber])
elif colors[neighber] == color_neighber: # 染色合规
continue
else: # 染色矛盾
return False
return True
for i in range(n): # 遍历每一个结点,也就是给其连通图染色
if colors[i] == 0: # 如果该结点未被染色,启动搜索对该连通图进行染色
if not bfs(i, red): # 给第一个结点染上红色
return False
return True
不额外增加函数版本:
from collections import deque
class Solution:
def isBipartite(self, graph: List[List[int]]) -> bool:
n = len(graph)
colors = [0] * n # 不需规定 red 或 green,考虑的时候想着给两个颜色赋相反值即可,
for i in range(n):
if colors[i] == 0:
colors[i] = 1 # 对当前结点染红色
queue = deque()
queue.append(i)
while queue: # 从当前结点 node 开始搜索当前连通图。只有当当前结点没被染色时才搜索,已经染色了就循环到graph的下一个结点
node = queue.popleft()
color = colors[node] # 注意是取当前结点的颜色,而不是虚变量 i
for neighber in graph[node]: # 遍历当前结点的所有邻接点
if colors[neighber] == 0: # 邻接点未染色就给染色
colors[neighber] = - color
queue.append(neighber)
elif colors[neighber] == color: # 邻接点颜色与结点 node 颜色相同,说明矛盾,不是二分图,直接返回false
return False
else: # 邻接点颜色与结点 node 颜色不同,说明已经入队过了,无需重复操作
continue
return True
作者:an-zhi-ruo-su
链接:https://leetcode.cn/problems/is-graph-bipartite/solution/bfs-zhi-xing-yong-shi-216-ms-zai-suo-you-python3-t/
时间复杂度:O(n+m),其中 n 和 m 分别是无向图中的点数和边数。
空间复杂度:O(n),存储结点颜色的数组需要 O(n) 的空间,并且在广度优先搜索的过程中,队列中最多有 n−1 个节点,需要 O(n) 的空间。
并查集
如果图是二分图的话,那么图中每个顶点的所有邻接点都应该属于同一集合,且不与顶点处于同一集合。因此可以使用并查集来解决这个问题:
遍历图中每个顶点,将当前顶点的所有邻接点进行合并,并判断这些邻接点中是否存在某一邻接点已经和当前顶点处于同一个集合中,若是,则说明不是二分图。
class unionfind:
def __init__(self,n):
self.father={}
for i in range(n):
self.father[i]=i
def find(self, u):
root_u=u
while self.father[root_u]!=root_u:
root_u=self.father[root_u]
return root_u
def union(self, u, v):
root_u=self.find(u)
root_v=self.find(v)
if root_u!=root_v:
self.father[root_u]=root_v
graph = [[1,3],[0,2],[1,3],[0,2]]
def isBipartite(graph):
n=len(graph)
uf=unionfind(n)
for u in range(n):
len_nei=len(graph[u])
for i in range(len_nei):
v1=graph[u][i]
# 如果遍历到另一个节点 u 时 发现 u 和它的某一个邻居 v 是联通的 则返回 False
if uf.find(u)==uf.find(v1):
return False
# 遍历每一个点,将该点的邻居结点连接起来
for j in range(i+1, len_nei):
v2=graph[u][j]
uf.union(v1, v2)
return True
作者:yuer-flyfly
链接:https://leetcode.cn/problems/is-graph-bipartite/solution/pan-duan-er-fen-tu-tu-pan-duan-wu-xiang-dqalo/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号