【树】力扣144:二叉树的前序遍历(附中序后序层序)
输入一个二叉树,输出一个数组,为二叉树前序遍历的结果。
示例:
输入:root = [1,null,2,3]
输出:[1,2,3]
二叉树遍历题目:
114. 二叉树的前序遍历
94. 二叉树的中序遍历
145. 二叉树的后序遍历
102. 二叉树的层序遍历
递归
递归的本质是栈的调用。
递归的模板相对比较固定,一般都会新增一个 dfs 函数:
def dfs(root):
if not root:
return None
res.append(root.val) # 前序遍历
dfs(root.left)
dfs(root.right)
对于前序、中序和后序遍历,只需将递归函数里的 res.append(root.val) 放在不同位置即可,然后在主函数中调用这个递归函数就可以了,代码完全一样。
前序
-
base case: 空树,即根结点为空
-
重复的子问题:先取根结点,再遍历左子树,最后遍历右子树
-
终止条件:当前结点为空
定义辅函数 preorder(node) 表示当前遍历到 node 结点的结果集。先将 node 结点的值加入结果集,然后递归调用 preorder(node.left) 来遍历 node 结点的左子树,再递归调用 preorder(node.right) 来遍历 node 结点的右子树。递归终止的条件为结点为空。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root: # base case
return []
res = []
def preorder(node):
if not node: # 递归终止条件
return None
res.append(node.val) # 将 node 结点的值加入结果集
preorder(node.left) # 遍历 node 结点的左子树
preorder(node.right) # 遍历 node 结点的右子树
preorder(root)
return res
单独辅函数版本,注意self:
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
res = []
self.preorder(root)
def preorder(self, root): # 加上 self
if root == None:
return
res.append(root.val)
self.preorder(root.left)
self.preorder(root.right)
时间复杂度:O(n),其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n),为递归过程中栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
中序
遍历顺序:左孩子 -> 根结点 -> 右孩子
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def dfs(root):
if not root:
return None
dfs(root.left)
res.append(root.val)
dfs(root.right)
dfs(root)
return res
后序
遍历顺序:左孩子 -> 右孩子 -> 根结点
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def dfs(root):
if not root:
return None
dfs(root.left)
dfs(root.right)
res.append(root.val)
dfs(root)
return res
迭代
递归是隐式地维护了一个栈,在迭代的时候就需要显式地将这个栈模拟出来。
迭代法就是不断地将旧的变量值,递推计算新的变量值。
前序
1. 常规解法
前序遍历的顺序是 根结点、左子树、右子树,也就是 先输出根结点,再输出左子树,最后输出右子树。
由于栈 “先入后出” 的特点,所以结合前序遍历的顺序,迭代的过程就是:每次都先将根结点放入栈,然后是右子树和左子树。
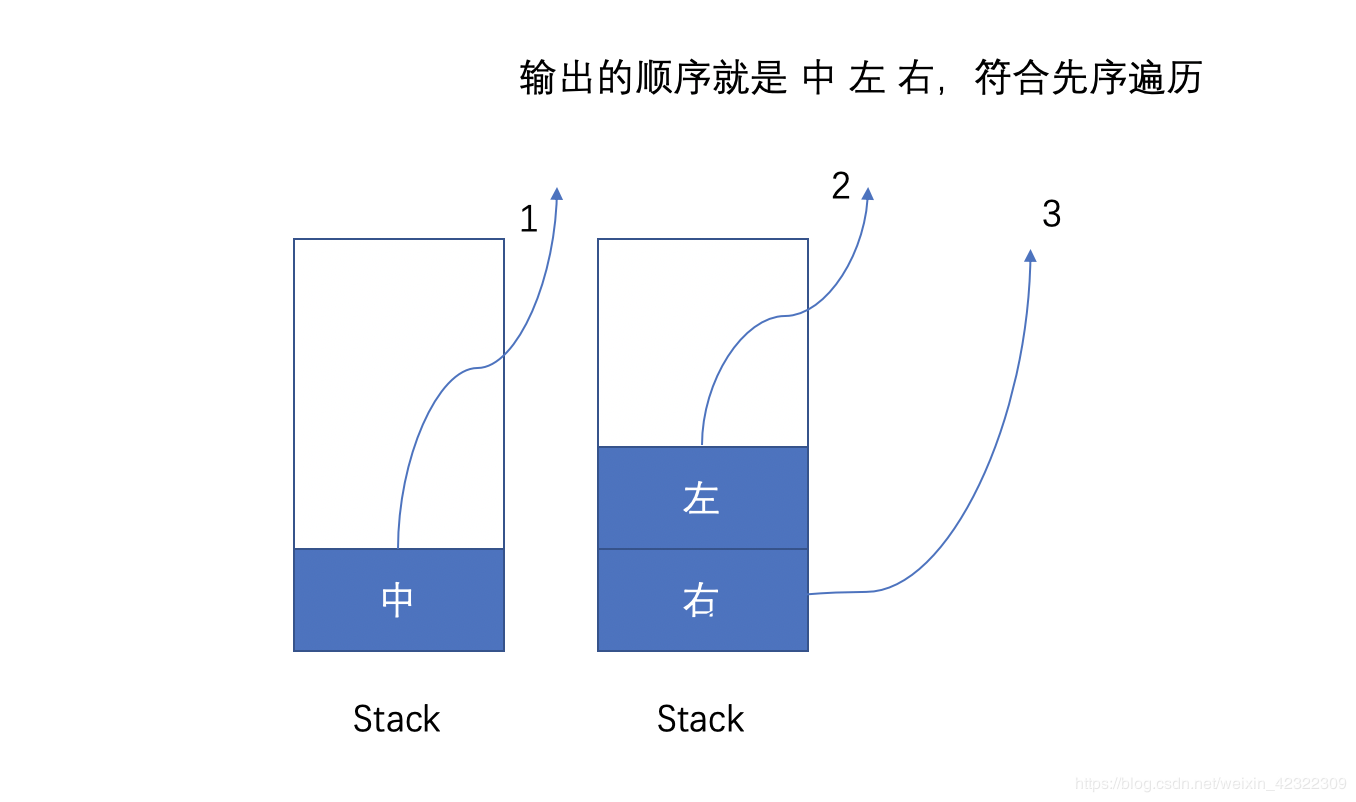
-
初始化维护一个栈 stack,先将根结点 root 入栈
stack = [root] -
当栈不为空时
- 弹出栈顶元素 node,将 node 结点的值加入结果集 res 中
node = stack.pop() res.append(node.val)- 若 node 的右子树不为空,右子树入栈
if node.right: stack.append(node.right)- 若 node 的左子树不为空,左子树入栈
if node.left: stack.append(node.left)
总体代码:
能够理解循环内的 node 不是 树的 root,也可以把 node 写为 root,在循环内这只是一个变量。
实际上就是dfs的实现
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
stack, res = [root], []
while stack:
node = stack.pop()
if node: # 可以不要这句判断
res.append(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return res
时间复杂度:O(n),其中 n 是二叉树的节点数。每一个结点恰好被遍历一次。
空间复杂度:O(n),为迭代过程中显式栈的开销,平均情况下为 O(logn),最坏情况下树呈现链状,为 O(n)。
这里的stack = [root],也可以写成
2. 模板解法
模板解法的思路稍有不同:
-
先将根结点 cur 和所有的左孩子入栈,并加入到结果集中,直至 cur 为空,用一个 while 循环实现
-
然后,每弹出一个栈顶元素 tmp,就到达它的右孩子,再将这个结点当作 cur 重新按上面的步骤来一遍,直至栈为空。这里又需要一个 while 循环
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
cur, stack, res = root, [], []
while cur or stack:
while cur: # 根结点和所有左孩子入栈,同时添加到结果集
stack.append(cur)
res.append(cur.val)
cur = cur.left
# 每弹出一个元素,就到达其右孩子
tmp = stack.pop()
cur = tmp.right
return res
中序
遍历顺序:左孩子 -> 根结点 -> 右孩子
和前序遍历的模板代码完全相同,只是在出栈的时候才将结点 tmp 的值加入到结果中。
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
cur, stack, res = root, [], []
while cur or stack:
while cur: # 根结点和所有左孩子入栈
stack.append(cur)
cur = cur.left
tmp = stack.pop()
res.append(tmp.val) # 出栈时再加入结点 tmp 的值
cur = tmp.right
return res
后序
模板解法
-
结点 cur 先到达最右端的叶子节点,并将路径上的结点入栈。
-
每次从栈中弹出一个元素后,cur 到达它的左孩子,并将左孩子看作 cur 继续执行上面的步骤。
-
最后将结果反向输出即可。
总体来讲就是和前序遍历的左右相反。
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
cur, stack, res = root, [], []
while cur or stack:
while cur: # 从根结点开始向右下遍历,先到达最右端叶子结点
stack.append(cur)
res.append(cur.val)
cur = cur.right
tmp = stack.pop()
cur = tmp.left
return res[::-1] # 反向输出
后序遍历采用模板解法并没有按照真实的栈操作,而是利用了结果的特点反向输出,显得技术含量不足。因此掌握标准的栈操作解法是必要的。
常规解法
类比前序遍历的常规解法,只需要将输出的“根 -> 左 -> 右”的顺序改为“左 -> 右 -> 根”就可以了。
如何实现呢?
有一个小技巧:入栈时额外加入一个标识,比如在栈中使用 flag == 0。每次从栈中弹出元素时,如果 flag 为 0,则需要将 flag 变为 1,并连同该结点再次入栈,只有当 flag 为 1 时才可将该结点加入到结果集中。
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if not root:
return []
stack, res = [(0, root)], [] # 在栈中添加 flag == 0,用小括号()
while stack:
flag, node = stack.pop()
if not node:
continue
if flag == 1: # 遍历过了,加入到结果集 res 中
res.append(node.val)
else:
stack.append((1, node))
# 先右再左
stack.append((0, node.right))
stack.append((0, node.left))
return res
层序
二叉树的层次遍历的迭代方法与前面不用,因为前面的都采用的是深度优先搜索的方式,而层次遍历使用的是广度优先搜索,广度优先搜索主要使用队列实现,也就不能使用前面的模板解法了。
广度优先搜索的步骤:
-
初始化队列 queue,并将根结点 root 加入到队列中
-
当 queue 不为空时:
-
从 queue 中弹出结点 node,加入到结果中
-
如果左子树非空,左子树加入 queue
-
如果右子树非空,右子树加入queue
-
此外,由于题目要求每一层保存在一个子数组中,所以额外加入变量 level 保存每层的遍历结果,并使用 for 循环来实现
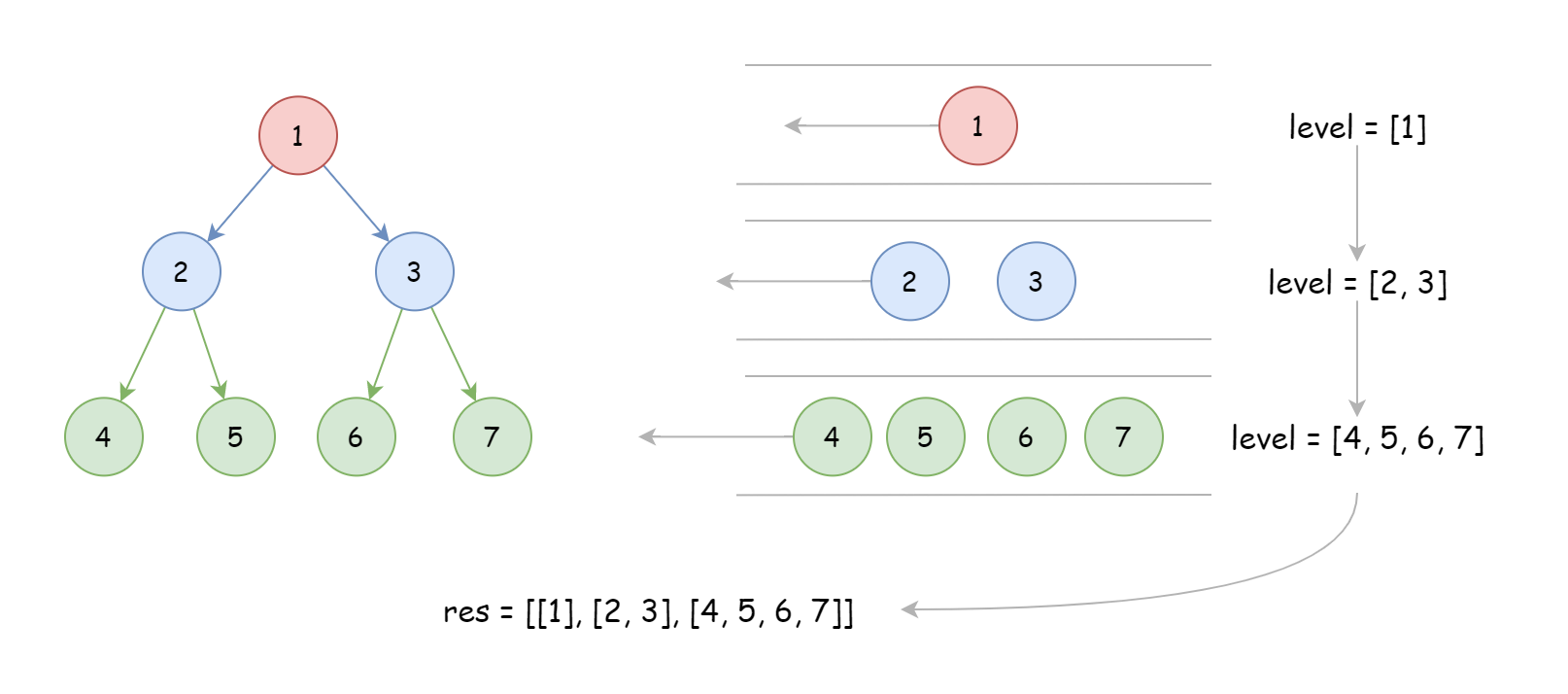
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
queue, res = [root], []
while queue:
level = []
for i in range(len(queue)):
node = queue.pop(0) # 这里的 queue 相当于一个队列,一端进另一端出。不是pop(),是pop(0)
level.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(level)
return res
Morris 中序遍历(常数空间)
用递归和迭代的方式都使用了辅助的空间,而莫里斯遍历的优点是没有使用任何辅助空间。
缺点是改变了整个树的结构,强行把一棵二叉树改成一段链表结构。
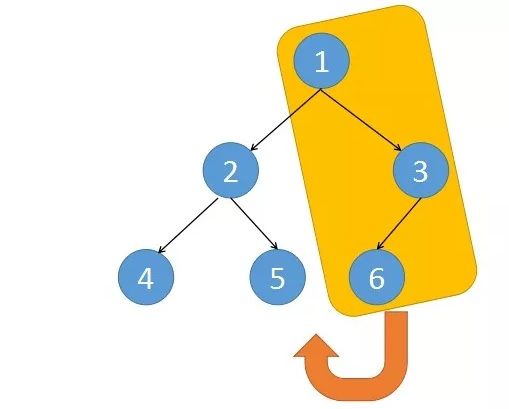
相当于将黄色区域部分挂到结点值为 5 的右子树上,接着再把 2 和 5 对应的这两个结点挂到 4 的右边。
这样整棵树基本上就变改成了一个链表了,之后再不断往右遍历。
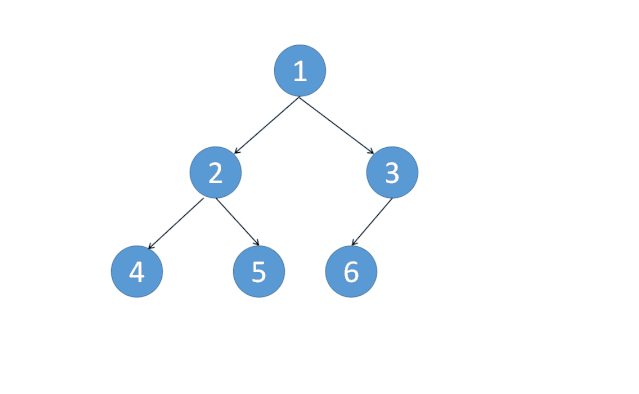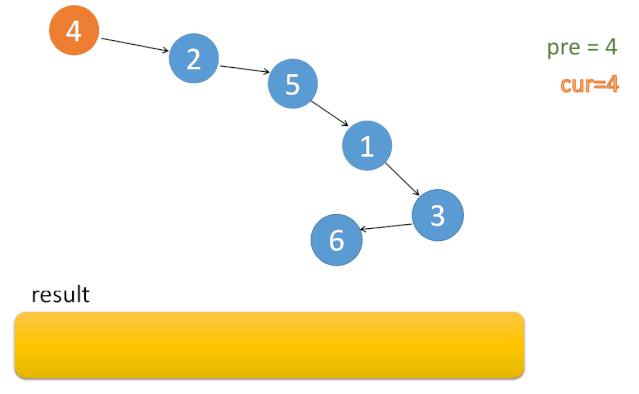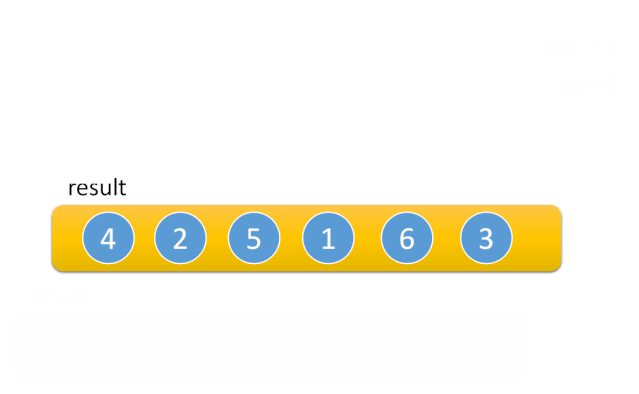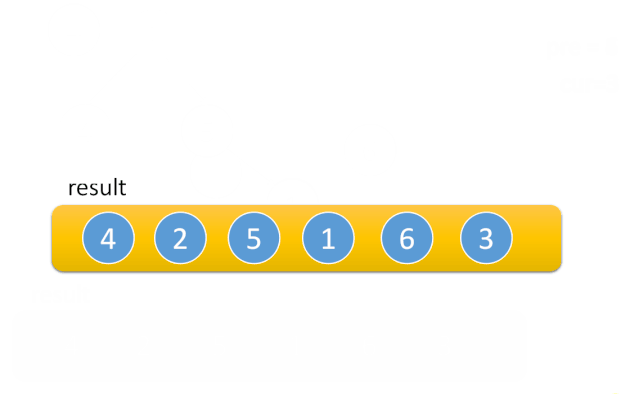
前置知识:
-
前驱结点:如果按照中序遍历访问树,访问的结果为 ABC,则称 A 为 B 的前驱结点,B 为 C 的前驱结点
-
前驱结点 predecessor(简写为pred)是 cur 左子树的最右子树(按照中序遍历走一遍就知道了)
-
由此可知,前驱结点的右子结点一定为空
主要思想:
-
树的链接是单向的,从根结点出发,只有通往子结点的单向路程
-
中序遍历迭代法的难点就在于:必须先访问当前结点的左子树,才能访问当前结点。但是只有通往左子树的单向路程,而没有回程路,因此无法进行下去,除非用额外的数据结构记录下回程的路
-
在这里可以利用当前结点的 前驱结点 建立回程的路,也不需要消耗额外的空间
-
根据前置知识的分析,当前结点的前驱结点的右子结点为空,因此可以用其保存回程的路
-
但是要注意,这是建立在破坏了树的结构的基础上的,因此最后还有一步“消除链接”的步骤,将树的结构还原
重点过程:当遍历到当前结点 cur 时,使用 cur 的前驱结点 pred
-
标记当前结点是否访问过
-
记录回溯到 cur 的路径(访问完 pred 以后,就应该访问 cur 了)
访问 cur 结点需要做的事:
-
访问 cur 结点的时候,先找其前驱结点 pred
-
找到前驱结点 pred 后,根据其右指针的值,来判断 cur 的访问状态
-
若 pred 的右子结点为空,说明 cur 第一次访问,其左子树还没有访问,此时应该将其指向cur,并访问 cur 的左子树
-
若 pred 的右子结点指向 cur,那么说明这是第二次访问 cur 了,也就是说其左子树已经访问完了,此时将 cur.val 加入结果集中
-
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return[]
res = []
pred, cur = None, root # 初始化前驱结点和当前结点(因为操作从 root 开始,也可以直接用 root 表示当前结点)
while cur:
# 若左结点不为空,就将当前结点连带右子树全部挂到左结点的最右子树下面
if cur.left:
pred = cur.left
while pred.right: # 右结点为空时说明到达了左子树的最右结点
pred = pred.right
pred.right = cur # 当前结点变为前驱结点的子结点
tmp = cur
cur = cur.left # 新的当前结点作为形状上的树的根结点
tmp.left = None
# 若左子树为空,则将这个结点加入结果集,并向右边遍历,一边输出一边检查是否所有结点都没有了左子树。如果有,则继续操作,没有则输出
else:
res.append(cur.val)
cur = cur.right
return res
作者:wang_ni_ma
链接:https://leetcode.cn/problems/binary-tree-inorder-traversal/solution/dong-hua-yan-shi-94-er-cha-shu-de-zhong-xu-bian-li/
时间复杂度:O(n),其中 n 为树的结点个数。找到每个前驱结点的复杂度是 O(n),因为 n 个结点的二叉树有 n − 1 条边,每条边只可能使用 2 次(一次定位到结点,一次找到前驱结点),因此总时间复杂度为 O(2n) = O(n)。
空间复杂度:O(1)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号