【字符串】力扣28:实现 strStr() (KMP/Sunday)
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回 -1 。
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。
示例1:
输入:haystack = "hello", needle = "ll"
输出:2
示例2:
输入:haystack = "aaaaa", needle = "bba"
输出:-1
本题是经典的字符串单模匹配的模型,因此可以使用字符串匹配算法解决,常见的字符串匹配算法包括 暴力匹配法、Knuth-Morris-Pratt 算法、Boyer-Moore 算法、Sunday 算法(BM的简化版)等。不用暴力匹配的话,本题是一道不是简单的简单题。
1 暴力匹配
让字符串 needle 与字符串 haystack 的所有长度为 m 的子串均匹配一次。
为了减少不必要的匹配,每次匹配失败即立刻停止当前子串的匹配,对下一个子串继续匹配。
如果当前子串匹配成功,返回当前子串的开始位置即可。如果所有子串都匹配失败,则返回 -1。
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
'''
实际上,题目说明了needle和haystack不是空字符串,前4行在本题是不需要的
'''
m, n = len(haystack), len(needle)
if not needle: # needle 是空字符串的特殊情况,即 n == 0
return 0
if not haystack or m < n: # haystack是空字符串 & 主串长度小于模式串长度的情况,可以降低实际操作时间
return -1
for i in range(m - n + 1): # 注意范围
flag = True
for j in range(n):
if haystack[i + j] != needle[j]:
flag = False
break
if flag: # haystack的某切片与needle匹配成功
return i
return -1
时间复杂度:O(nm),其中 n 是字符串 haystack 的长度,m 是字符串 needle 的长度。最坏情况下需要将字符串 needle 与字符串 haystack 的所有长度为 m 的子串均匹配一次。
空间复杂度:O(1)。只需要常数的空间保存若干变量。
python黑科技
find()函数赛高!使用的是BMHBNFS算法
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
return haystack.find(needle)
但很明显,题目的意思不会是想让答题者用内置函数一下子得到结果,而是如何实现这个find()函数。
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
m, n = len(haystack), len(needle)
for i in range(m):
if haystack[i: n + i] == needle: # if haystack[i: n + i] == needle[:]:
return i
return -1
但是!针对python语言,用切片haystack[i: n + i] == needle来实现也属于投机取巧,题目考的当然是这一步怎么比较的。
index函数也有用!
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
try:
return haystack.index(needle)
except ValueError:
return -1
以上投机取巧的方法突破算例实际所用时间和空间和朴素的暴力破解法差不多。
2 KMP算法
KMP 算法是由 Knuth、Morris和Pratt 三位学者发明的,取了三位学者名字的首字母,所以叫做 KMP。
KMP 主要应用在字符串匹配上。主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配。
KMP的时间复杂度为 O(m + n)。其中 n 为文本串长度,m 为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n);之前还要单独生成next数组,时间复杂度是O(m)。暴力的解法显而易见是 O(n * m),所以 KMP 在字符串匹配中极大提高了搜索效率。
如何记录已经匹配的文本内容,是KMP的重点,也是next数组肩负的重任。
没有彻底搞懂,懵懵懂懂就把代码背下来太容易忘了。不仅面试的时候可能写不出来,如果面试官问:next数组里的数字表示的是什么,为什么这么表示?答不上来。
2.1 前缀表
next数组 就是一个前缀表(prefix table)。
前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串可以往后移动的最大步长。
前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力,所以要用前缀表。
举个例子:
要在文本串 t = aabaabaafa 中查找是否出现过一个模式串 s = aabaaf。(记住文本串和模式串的作用,对于理解下文很重要,要不然容易看懵)
2.1.1 前缀表计算
-
字符串的前缀是指 所有以第一个字符开头的连续子串,即从串首开始到某个位置 i 结束
-
字符串的后缀是指 所有以最后一个字符结尾的连续子串,即从某个位置 i 开始到整个串末尾结束
-
真前(后)缀是指 不包含自身的前(后)缀
-
前缀函数是指 某个字符串中真后缀同时也是它的真前缀的最长子串的长度
举例:字符串 aabaaf
首先,不考虑空字符,所有的前缀有 a, aa, aab, aaba, aabaa, aabaaf,其中真前缀有 a, ab, aba, abab;所有的后缀有 f, af, aaf, baaf, abaaf, aabaaf,其中真后缀有 f, af, aaf, baaf, abaaf
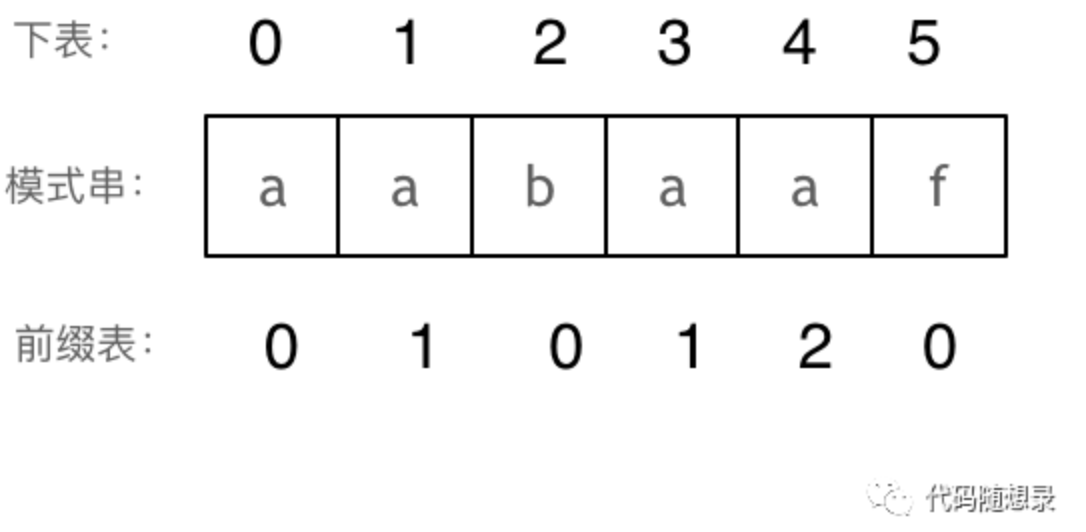
依旧以字符串 aabaaf 为例,计算其最长相同真前后缀来求其前缀表。
- 子串a
前缀有 a,没有真后缀。没有与真后缀相同的前缀,因此前缀函数为 0。 - 子串aa
前缀有 a, aa,真后缀有 a。前缀 a 与真后缀 a 相同,因此前缀函数为 1。 - 子串aab
前缀有 a, aa, aab,真后缀有 b, ab。没有与真后缀相同的前缀,因此前缀函数为 0。 - 子串aaba
前缀有 a, aa, aab, aaba,真后缀有 a, ba, aba。前缀 a 与真后缀 a 相同,因此前缀函数为 1。 - 子串aabaa
前缀有 a, aa, aab, aaba, aabaa,真后缀有 a, aa, baa, abaa。前缀 a 与真后缀 a 相同,前缀 aa 与真后缀 aa 相同,有两个真前缀与真后缀相同的子串,其中第二个子串最长,长度为2,因此前缀函数为 2。注意:不是满足要求的字串的个数,而是满足要求的最长字串的长度 - 子串aabaaf
前缀有 a, aa, aab, aaba, aabaa, aabaaf,真后缀有 f, af, aaf, baaf, abaaf。没有与真后缀相同的前缀,因此前缀函数为 0。
2.1.2 前缀表应用
再来看如何 利用前缀表找到 当字符不匹配的时候应该指针应该移动的位置:

找到了不匹配的位置, 此时要看它的前一个字符的前缀表的数值是多少。
为什么要前一个字符的前缀表的数值呢?因为要找前面字符串的最长相同的真前缀和真后缀。
前一个字符的前缀表的数值是2, 所以把下标移动到下标 2 的位置继续匹配。最后就在文本串中找到了和模式串匹配的子串。
2.2 前缀表与next数组
很多KMP算法都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组可以直接是前缀表。但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
为什么这么做呢?其实这并不涉及到KMP的原理,而是具体实现。
2.2.1 -1 构造前缀表统一减一的next数组
C++代码
定义一个函数 getNext 来构建next数组,函数参数为 指向next数组的指针 和 一个字符串(文本串or模式串)。
void getNext(int* next, const string& t)
构造next数组其实就是 计算模式串 s 的前缀表 的过程。主要有三步:
- 初始化
定义两个指针 i 和 j,j 指向真前缀终止位置(严格来说是真前缀终止位置减一的位置,j+1 指向真前缀终止位置),i 指向真后缀终止位置。
然后对next数组进行初始化赋值:
int j = -1;
next[0] = j;
next[i] 表示 i(包括 i)之前最长相等的真前后缀长度(其实就是 j),所以 next[i] = j,且初始化 next[0] = j。
- 处理真前后缀不相同的情况
因为 j 初始化为 -1,那么 i 就从 1 开始,进行 s[i] 与 s[j+1] 的比较。所以遍历模式串 s 的循环下标 i 要从 1 开始。
for(int i = 1; i < s.size(); i++) {
如果 s[i] 与 s[j+1] 不相同,也就是 真前后缀的末尾不相同,就要向前回溯。
怎么回溯呢?
既然 next[j] 记录着 j(包括 j)之前的子串的相同真前后缀的长度。那么 s[i] 与 s[j+1] 不相同,就要找 j+1 的前一个元素 在 next数组 里的值,即 next[j]。
while (j >= 0 && s[i] != s[j + 1]) { # 真前后缀不相同时
j = next[j]; # 向前回溯
}
- 处理前后缀相同的情况
如果 s[i] 与 s[j + 1] 相同,那么就同时向后移动 i 和 j 说明找到了相同的真前后缀,同时还要将 j(真前缀的长度)赋给 next[i], 因为 next[i] 要记录相同真前后缀的长度。
if (s[i] == s[j + 1]) { // 前后缀相同时
j++;
}
next[i] = j;
构建前缀表统一减一的next数组的整体代码
void getNext(int* next, const string& s){
int j = -1; # j 指向前缀终止位置(严格来说是前缀终止位置减一的位置),i 指向后缀终止位置(前缀终止位置减一的位置)
next[0] = j;
for(int i = 1; i < s.size(); i++) { # 注意:i 从1开始
while (j >= 0 && s[i] != s[j + 1]) { # 前后缀 s[j+1] 与 s[i] 不相同
j = next[j]; # 向前回溯(关键)
}
if (s[i] == s[j + 1]) { # 前后缀相同
j++;
}
next[i] = j; # 将 j(前缀的长度)赋给 next[i],i 循环结束即形成next数组
}
}
作者:carlsun-2
链接:https://leetcode.cn/problems/implement-strstr/solution/dai-ma-sui-xiang-lu-kmpsuan-fa-xiang-jie-mfbs/
此时如果输入的模式串为aabaaf,对应的next为 -1 0 -1 0 1 -1,前文得出的前缀表为 0 1 0 1 2 0,正好是next数组中每个元素加一的结果。(这里 j 和 next[0] 初始化为 -1,整个next数组是以 前缀表减一之后的效果来构建的。)
对应的图形解释
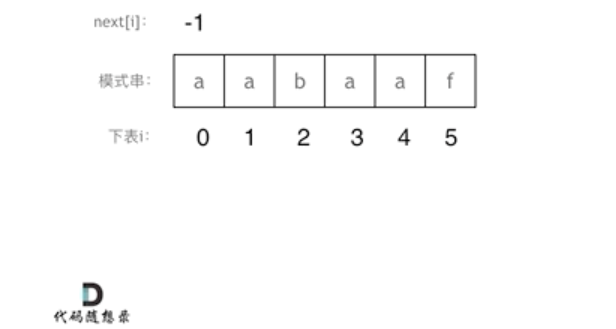
初始化真前缀指针 j = -1,即 j + 1 = 0。
next[i] 表示 i(包括 i)之前最长相等的真前后缀长度,所以 i == 0 时 next[0] = j == -1 。然后 i 开始在范围 [1, len(s)) 内循环。
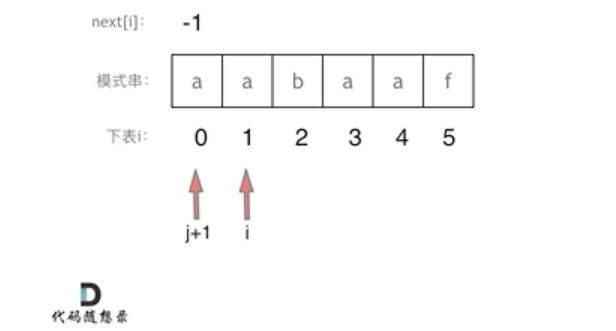
i == 1时 j + 1 == 0, 真后缀s[1] == 真前缀s[0],因此 执行 j++,此时 j 值为 0,next[1] = j == 0,i 继续循环。
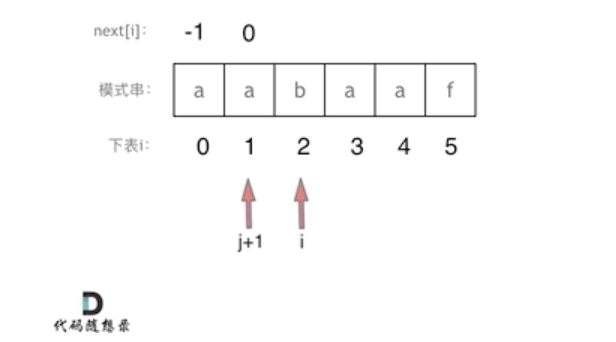
i == 2时 j + 1 == 1,真后缀s[2] != 真前缀s[1],因此 向前回溯,即执行 j = next[j] == -1;继续用真后缀s[2]与真前缀比较。
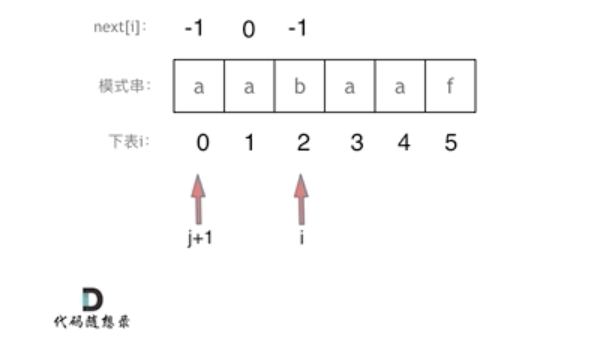
i == 2时 j + 1 == 0,真后缀s[2] != 真前缀s[0],此时真前缀指针 j 无法继续向前移动,因此 next[2] = j == -1;j 不变,i 继续循环。
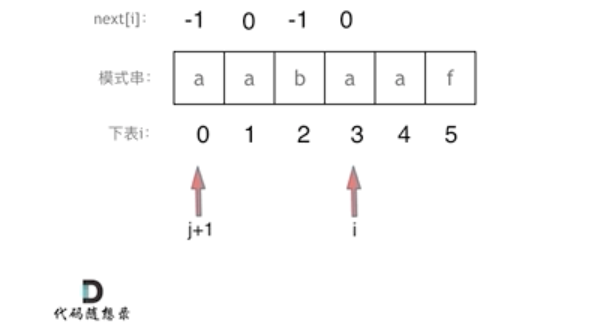
i == 3时 j + 1 == 0,真后缀s[3] == 真前缀s[0],因此 执行 j++,此时 j 值为 0,next[3] = j == 1,i 继续循环。
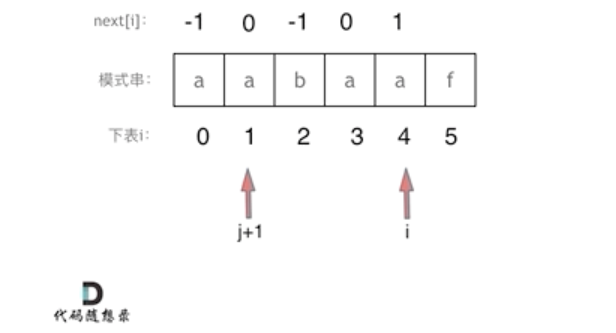
i == 4时 j + 1 == 1,真后缀s[4] == 真前缀s[1],因此 执行 j++,此时 j 值为 1,next[4] = j == 0,i 继续循环。
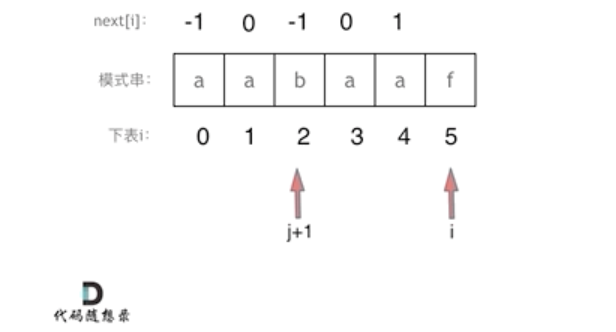
i == 5时 j + 1 == 2,真后缀s[5] != 真前缀s[2],因此 向前回溯,即执行 j = next[j] == 0;继续用真后缀s[5]与前缀比较。
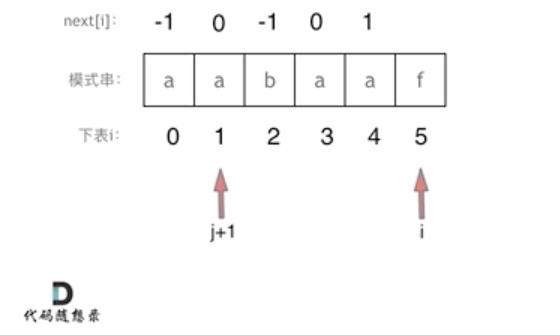
i == 5时 j + 1 == 1,真后缀s[5] != 真前缀s[1],因此 向前回溯,即执行 j = next[j] == -1;继续用真后缀s[5]与前缀比较。
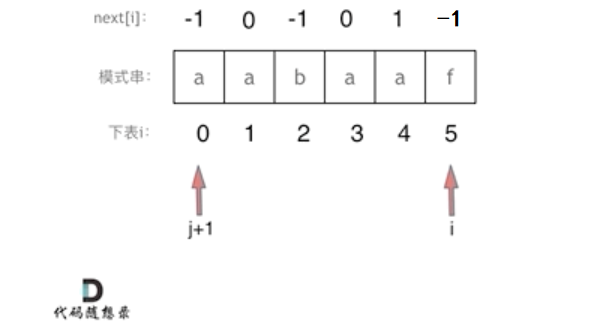
i == 5时 j + 1 == 0,真后缀s[5] != 真前缀s[0],此时真前缀指针 j 无法继续向前移动,因此 next[5] = j == -1。
此时 i 指针已经指向模式串 s 的最后一个元素,循环结束。
2.2.1 -2 使用前缀表统一减一的next数组做匹配
得到next数组之后,就要用它做匹配了。
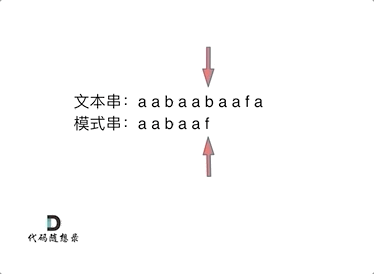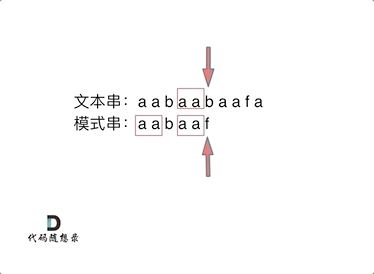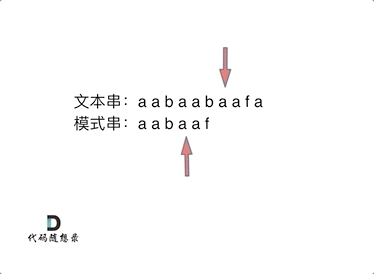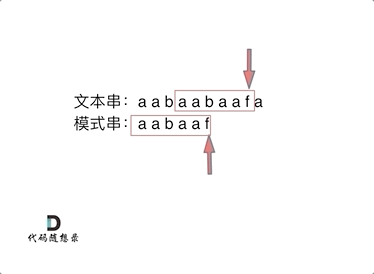
定义两个指针: j(严格来说是 j + 1)指向模式串 s 起始位置,i 指向文本串 t 起始位置。那么 i 从 0 开始,j 初始值依然为-1。
为什么呢?依然因为next数组里记录的指针 j 的起始位置为-1。
for (int i = 0; i < t.size(); i++)
接下来就是比较 t[i] 与 s[j + 1](因为 j 从 -1 开始)。
- 如果 t[i] 与 s[j + 1] 不同,j 就要从next数组里寻找下一个匹配的位置
while(j >= 0 && t[i] != s[j + 1]) { # 只有当 s[j + 1] == t[i]后,指针 j 才会移动,同时值加一变为 1;否则只有指针 i 在为了文本串 t 的第一个匹配元素而变化
j = next[j];
}
- 如果 t[i] 与 s[j + 1] 相同,那么 i 和 j 同时移动
if (t[i] == s[j + 1]) {
j++; # i的增加在for循环里
}
如何判断在文本串 t 里出现了模式串 s 呢?
如果 j 指向了模式串 s 的末尾,即 j == s.size(),那么就说明模式串 s 完全匹配文本串 t 里的某个子串了。
本题要在文本串字符串中找出模式串出现的第一个位置 (从 0 开始),所以return 当前在文本串匹配模式串的位置 i 减去 s.size()。
if (j == (s.size() - 1) ) {
return (i - s.size() + 1);
}
使用前缀表统一减一的next数组用模式串匹配文本串的整体代码:
int j = -1; # 因为next数组里记录的起始位置为-1
for (int i = 0; i < t.size(); i++) { # 注意:i 从0开始,范围在文本串 t 的长度内
while(j >= 0 && t[i] != s[j + 1]) { # 不匹配
j = next[j]; # j 寻找之前匹配的位置
}
if (t[i] == s[j + 1]) { # 若匹配,j 和 i 同时向后移动
j++;
}
if (j == (s.size() - 1) ) { # 文本串 t 里出现了模式串 s
return (i - s.size() + 1); # 注意 +1
}
}
作者:carlsun-2
链接:https://leetcode.cn/problems/implement-strstr/solution/dai-ma-sui-xiang-lu-kmpsuan-fa-xiang-jie-mfbs/
2.2.2 -1 构建和使用前缀表不减一的next数组
next数组仅仅涉及到KMP算法实现上的问题,如果想直接使用前缀表,可以换一种回退方式,用 j = next[j-1] 来进行回退。j = next[x] 这一步最为关键!
本题完整C++代码:
class Solution {
public:
'''
自定义函数getNext来构建next数组,函数参数为 指向next数组的指针 & 模式串
'''
void getNext(int* next, const string& s) {
int j = 0; # 初始化指针 j 为 0
next[0] = j;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) { # j 要保证大于 0,不能等于 0 了,因为下面有取 j-1 作为数组下标的操作。与真后缀相比较的真前缀为 s[j]
j = next[j - 1]; # 注意这里,是要找前一位的对应的回退位置了
}
if (s[i] == s[j]) { # 与真后缀相比较的真前缀为 s[j]
j++;
}
next[i] = j;
}
}
'''
此时如果输入的模式串为aabaaf,对应的next为 0 1 0 1 2 0(其实这就是前缀表的数值了)
用这样的next数组也可以用来做匹配,代码要有所改动
'''
int strStr(string haystack, string needle) {
if (needle.size() == 0) { # 考虑模式串为空的特殊情况
return 0;
}
int next[needle.size()]; # getNext函数中要用到next数组和模式串的长度,所以要在调用函数前定义
getNext(next, needle); # 调用getNext函数,得到模式串 needle 的前缀表
'''
使用next数组做匹配
'''
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
j = next[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == needle.size()) {
return (i - needle.size() + 1);
}
}
return -1;
}
};
作者:carlsun-2
链接:https://leetcode.cn/problems/implement-strstr/solution/dai-ma-sui-xiang-lu-kmpsuan-fa-xiang-jie-mfbs/
2.2.2 -2 构建和使用前缀表不减一的next数组(不构建新函数)
官解也用了KMP算法,但是没有自定义新函数,也就不存在函数调用了。理解了上文之后发现这一版代码更简单一些。
步骤1. 求模式串 needle 的前缀函数,需要保留这部分的前缀函数值。
步骤2. 求文本串 haystack 的前缀函数,无需保留这部分的前缀函数值,只需要用一个变量记录上一个位置的前缀函数值即可。当某个位置的前缀函数值等于模式串 needle 的长度时,说明找到了一次字符串 needle 在字符串 haystack 中的出现(因为此时真前缀恰为字符串 needle,真后缀为以当前位置为结束位置的字符串 haystack 的子串)。计算出起始位置,将其返回即可。
@ C++
class Solution {
public:
int strStr(string haystack, string needle) {
int n = haystack.size(), m = needle.size();
if (m == 0) { # 特殊情况
return 0;
}
'''
步骤1:求模式串 needle 的前缀函数,并需要保留这部分的前缀函数值
'''
vector<int> pi(m);
for (int i = 1, j = 0; i < m; i++) {
while (j > 0 && needle[i] != needle[j]) {
j = pi[j - 1];
}
if (needle[i] == needle[j]) {
j++;
}
pi[i] = j;
}
'''
步骤2:求文本串 haystack 的前缀函数,并用一个变量记录上一个位置的前缀函数值。
当某个位置的前缀函数值 等于 模式串 needle 的长度 时,计算出起始位置,将其返回
'''
for (int i = 1, j = 0; i < n; i++) {
while (j > 0 && haystack[i] != needle[j]) {
j = pi[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == m) {
return i - m + 1; # 存在匹配的子字符串时返回起始位置,注意 +1
}
}
return -1; # 不存在匹配的子字符串则返回-1
}
};
作者:LeetCode-Solution
链接:https://leetcode.cn/problems/implement-strstr/solution/shi-xian-strstr-by-leetcode-solution-ds6y/
2.3 python代码
2.3.1 前缀表统一减一的方法
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
a=len(needle)
b=len(haystack)
if a==0:
return 0
next=self.getnext(a,needle)
p=-1
for j in range(b):
while p>=0 and needle[p+1]!=haystack[j]:
p=next[p]
if needle[p+1]==haystack[j]:
p+=1
if p==a-1:
return j-a+1
return -1
def getnext(self,a,needle):
next=['' for i in range(a)]
k=-1
next[0]=k
for i in range(1,len(needle)):
while (k>-1 and needle[k+1]!=needle[i]):
k=next[k]
if needle[k+1]==needle[i]:
k+=1
next[i]=k
return next
作者:carlsun-2
链接:https://leetcode.cn/problems/implement-strstr/solution/dai-ma-sui-xiang-lu-kmpsuan-fa-xiang-jie-mfbs/
2.3.2 前缀表不减一的方法
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
a=len(needle)
b=len(haystack)
if a==0:
return 0
i=j=0
next=self.getnext(a,needle)
while(i<b and j<a):
if j==-1 or needle[j]==haystack[i]:
i+=1
j+=1
else:
j=next[j]
if j==a:
return i-j
else:
return -1
def getnext(self,a,needle):
next=['' for i in range(a)]
j,k=0,-1
next[0]=k
while(j<a-1):
if k==-1 or needle[k]==needle[j]:
k+=1
j+=1
next[j]=k
else:
k=next[k]
return next
作者:carlsun-2
链接:https://leetcode.cn/problems/implement-strstr/solution/dai-ma-sui-xiang-lu-kmpsuan-fa-xiang-jie-mfbs/
时间复杂度:O(n+m),其中 n 是字符串 haystack 的长度,m 是字符串 needle 的长度。至多需要遍历两字符串一次。
空间复杂度:O(m),其中 m 是字符串 needle 的长度。只需要保存字符串 needle 的前缀函数。
3 Sunday算法
来源:https://leetcode.cn/problems/implement-strstr/solution/python3-sundayjie-fa-9996-by-tes/
3.1 偏移表
偏移表的作用是存储每一个在 模式串 中出现的字符,在 模式串 中出现的最右位置到尾部的距离 +1,或 模式串长度 - 该字符最右出现的位置(从 0 开始)。即:
例如 aab:
模式串长度为len(pattern) = 3;
a 的最右位置为 1,到尾部的距离为 1,则偏移位是最右位置到尾部的距离 + 1 = 1 + 1 = 2,或 模式串长度 - 该字符最右出现的位置 = 3- 1 = 2;
b 的最右位置为 2,到尾部的距离为 0,则偏移位是最右位置到尾部的距离 + 1 = 1 + 1 = 2,或 模式串长度 - 该字符最右出现的位置 = 3- 2 = 1;
其他的均为 最右位置到尾部的距离 + 1 = 3 + 1 = 4,或 模式串长度 - 该字符最右出现的位置 = 3 - (-1) = 4
3.2 Sunday 匹配机制
匹配机制非常容易理解:
目标字符串 String
模式串 Pattern
当前查询索引 idx(初始为 0)
待匹配字符串 str_cut: String [idx: idx + len(Pattern)]
每次匹配都会从 目标字符串中 提取 待匹配字符串 与 模式串 进行匹配(循环到 idx + len(pattern) > len(String)):
-
若匹配,返回当前 idx
-
不匹配,则查看 待匹配字符串 的下一位字符 c:
-
若 c 存在于 Pattern 中,idx = idx + 偏移表[c]。即 idx 的移动位数 = 模式串长度 - 该字符最右出现的位置(从 0 开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。
相当于使得模式串的 c 对齐 待匹配字符串的 c。所以偏移表的作用是告诉我们下一步可能匹配需要移动的最大步数 -
若 c 不存在于 Pattern 中,则 idx = idx + len(pattern) + 1。即直接跳过字符 c ,idx 的移动位数 = 模式串长度 + 1
-
最坏情况:O(mn)
平均情况:O(n)
举例:
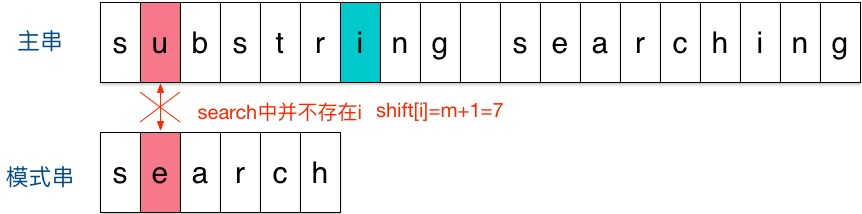
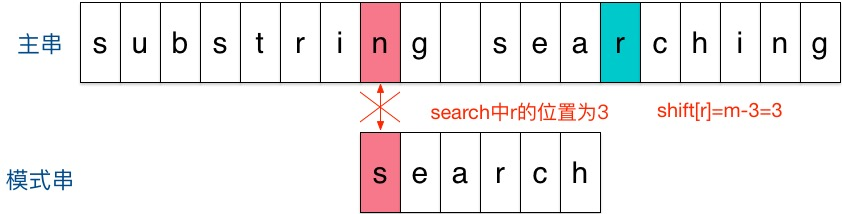
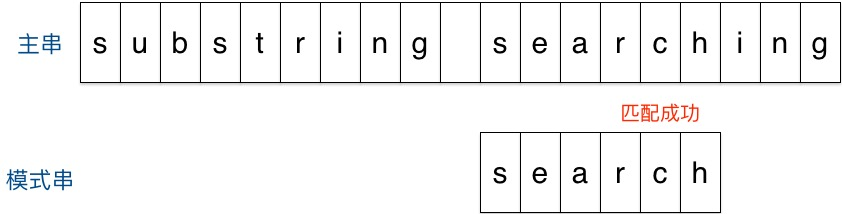
题目python代码:
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
# Func: 计算偏移表
def calShiftMat(st):
dic = {}
for i in range(len(st)-1,-1,-1):
if not dic.get(st[i]):
dic[st[i]] = len(st)-i
dic["ot"] = len(st)+1
return dic
# 其他情况判断
if len(needle) > len(haystack): return -1
if needle == "": return 0
# 偏移表预处理
dic = calShiftMat(needle)
idx = 0
while idx + len(needle) <= len(haystack):
# 待匹配字符串
str_cut = haystack[idx:idx+len(needle)]
# 判断是否匹配
if str_cut==needle:
return idx
else:
# 边界处理
if idx+len(needle) >= len(haystack):
return -1
# 不匹配情况下,根据下一个字符的偏移,移动idx
cur_c = haystack[idx+len(needle)]
if dic.get(cur_c):
idx += dic[cur_c]
else:
idx += dic["ot"]
return -1 if idx+len(needle) >= len(haystack) else idx
作者:Tes
链接:https://leetcode.cn/problems/implement-strstr/solution/python3-sundayjie-fa-9996-by-tes/
评论区改进版本
'''
计算偏移表词典一行感觉就可以了。ot 值其实多余
边界处理第一行条件 = 就可以了 不可能出现 > 情况,因为 while 已经判断过了
return只为 -1 就可以,不再需要判断
'''
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
# 特殊情况先考虑
if not needle:
return 0
m, n = len(haystack), len(needle)
if n > m or m == 0:
return -1
# 偏移表预处理
shift = {char: n - j for j, char in enumerate(needle)}
idx = 0
while idx + n <= m:
# 获取待匹配字符串
str_cut = haystack[idx: idx + n]
# 判断是否匹配
if str_cut == needle: # 匹配成功,返回idx
return idx
elif idx + n >= m: # 边界情况一定要考虑,如果满足这个条件,那么不存在下一步找待匹配字符串的下一个字符 c 的操作
return -1
elif idx + n < m:
# 不匹配情况下,根据待匹配字符串下一个字符的偏移,移动 idx
nextc = haystack[idx + n] # 找到待匹配字符串的下一个字符 c
if shift.get(nextc): # c 存在于模式串 needle 中就说明偏移表shift里也存储了 c
idx += shift[nextc]
else: # c 不存在于模式串 needle 中
idx += n + 1
return -1


 浙公网安备 33010602011771号
浙公网安备 33010602011771号