【前缀和与积分图】力扣560：和为 K 的子数组()

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。
示例1：

输入：nums = [1,1,1], k = 2
输出：2

示例2：

输入：nums = [1,2,3], k = 3
输出：2

由题意：① 数组元素可以重复使用；② 一次求和可以使用1 ~ n个元素。

方法1. 枚举

考虑以 i 结尾和为 k 的连续子数组个数，我们需要统计符合条件的下标 j 的个数，其中 0≤j≤i 且 [j..i] 这个子数组的和恰好为 k 。

可以枚举 [0...i] 里所有的下标 j 来判断是否符合条件，这里有两种方式：

• 确定子数组的开头 i 和结尾 j ，除了两层for循环，还需要 O(n) 的时间复杂度遍历子数组来求和，复杂度就将达到 O(n^3) 从而无法通过所有测试用例

for i in range(n):
    for j in range(i, n):
        if sum(nums[i: j+1]) == k:
            count += 1

因此可以优化求和环节

for i in range(n):
    sum = 0
    for j in range(i, n):
        sum += nums[j]
        if sum == k:
            count += 1

这样，时间复杂度降到了 O(n^2)，但是在python3中其实依然会超时。

• 倒推：确定子数组的开头 i ，j 从 i 开始向前遍历，这样就是在已经知道 [j, i] 子数组的和的情况下，就能 O(1) 推出 [j-1, i] 的和，因此这部分的遍历求和是不需要的，在枚举下标 j 的时候已经能 O(1) 求出 [j, i] 的子数组之和。

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        n = len(nums)
        count = 0
        for i in range(0, n):
            sum = 0
            for j in range(i, -1, -1):
                sum += nums[j]
                if sum == k:
                    count += 1 # 注意这后面不能为了省时间而加上break，因为也许继续编历时前面的元素相互抵消而二次、三次满足前缀和为k的情况
        return count

时间复杂度：O(n^2)，其中 n 为数组的长度。枚举子数组开头和结尾需要 O(n^2) 的时间，其中求和需要 O(1) 的时间复杂度，因此总时间复杂度为 O(n^2)。

空间复杂度：O(1)。只需要常数空间存放若干变量。

方法2. 前缀和

先遍历一次数组，求出前缀和数组。之后这个数组可以代替暴力破解。但是很遗憾，时间复杂度还是O(n^2)。

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        n = len(nums)
        count = 0
        preSum = [0]
        # 求长度为 n+1 的前缀和数组preSum
        for num in nums:
            preSum.append(preSum[-1] + num)
        # 求区间和(前 j 个数之和减去前 i-1 个数之和)
        for i in range(1, n + 1):
            for j in range(i, n + 1):
                if preSum[j] - preSum[i - 1] == k:
                    count += 1
        return count

方法3. 前缀和 + 哈希表

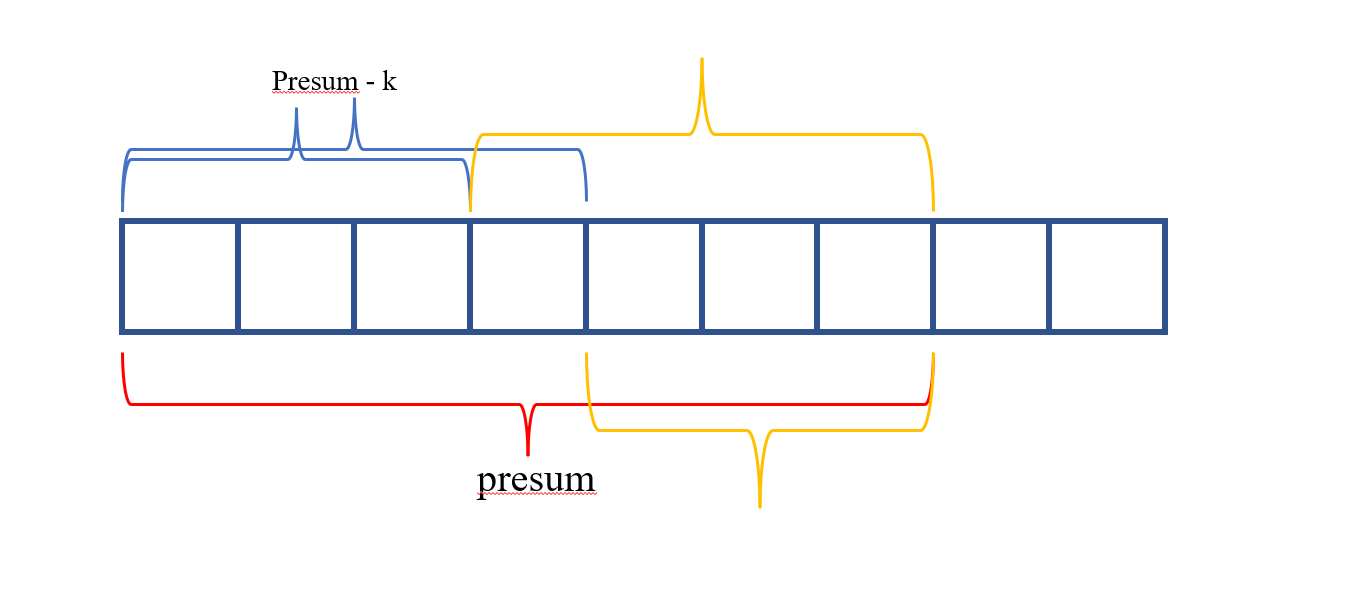
进一步优化，就是可以边算前缀和，边统计。可以利用 hashtable 记录前缀和来避免重复计算。在遍历到位置 i 时，当前的前缀和是 preSum，那么 hb[preSum-k] 即为以当前位置结尾、满足条件的区间个数。

• 维护一个 hashtable，key 为前缀和preSum，value 为 preSum 出现的次数
• 迭代数组，然后不断更新 preSum 和 hashtable
  • 如果 preSum 等于 k，那么很明显 count 应该 +1
  • 如果 preSum - k 在此时的 hashtable 中存在，就把这个前缀和已经出现的次数加到 count
    
    

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        count, preSum = 0, 0
        ht = {} # 建立哈希表
        for num in nums:
            preSum += num # 更新前缀和
            if preSum == k:
                count += 1
            if preSum - k in ht:
                count += ht[preSum - k]
            '''
            更新哈希表
            以下代码的一行实现 ht[preSum] = ht.get(preSum, 0) + 1
            '''
            if preSum in ht:
                ht[preSum] += 1
            else:
                ht[preSum] = 1
        return count

时间复杂度：O(n)，其中 n 为数组的长度。遍历数组的时间复杂度为 O(n)，中间利用哈希表查询删除的复杂度均为 O(1)，因此总时间复杂度为 O(n)。

空间复杂度：O(n)，其中 n 为数组的长度。哈希表在最坏情况下可能有 n 个不同的键值，因此需要 O(n) 的空间复杂度。

思路相同，不需要多级判断的方法：

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        # 要求的连续子数组
        count = 0
        n = len(nums)
        preSums = collections.defaultdict(int)
        preSums[0] = 1
        presum = 0
        for i in range(n):
            presum += nums[i]
            # if preSums[presum - k] != 0:
            count += preSums[presum - k]   # 利用 defaultdict 的特性，当 presum-k 不存在时，返回的是0，避免了判断
            preSums[presum] += 1  # 给前缀和为presum的个数加1
        return count

作者：wu-qiong-sheng-gao-de-qia-nong
链接：https://leetcode.cn/problems/subarray-sum-equals-k/solution/python3-by-wu-qiong-sheng-gao-de-qia-non-w6jw/