【前缀和与积分图】力扣304：二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：
计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。
实现 NumMatrix 类：
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

示例：

输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
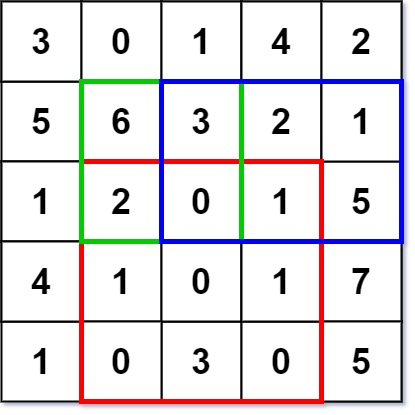
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

方法1. 对每一行计算一维前缀和

将第 303 题的做法应用于这道题，初始化时对矩阵的每一行计算前缀和，检索时对二维区域中的每一行计算子数组和，然后对每一行的子数组和计算总和。
具体实现方面，创建 m 行 n+1 列的二维数组 preSum，其中 m 和 n 分别是矩阵 matrix 的行数和列数，preSum[i] 为 matrix[i] 的前缀和数组。将 preSum 的列数设为 n+1 的目的是为了方便计算每一行的子数组和，不需要对 \(col_{1}\)=0 的情况特殊处理。

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        self.preSum = [[0] * (n + 1) for _ in range(m)]
        for i in range(m):
            for j in range(n):
                self.preSum[i][j + 1] = self.preSum[i][j] + matrix[i][j]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
    for i in range(row1, row2 + 1))：
        res = sum(self.preSum[i][col2 + 1] - self.preSum[i][col1]
        return res

# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

时间复杂度：初始化 O(mn)，每次检索 O(m)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。初始化需要遍历矩阵 matrix 计算二维前缀和，时间复杂度是 O(mn)。每次检索需要对二维区域中的每一行计算子数组和，二维区域的行数不超过 m，计算每一行的子数组和的时间复杂度是 O(1)，因此每次检索的时间复杂度是 O(m)。
空间复杂度：O(mn)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。需要创建一个 m 行 n+1 列的前缀和数组 preSum。

方法2. 对整个矩阵计算二维前缀和

方法1虽然利用了前缀和，但是每次检索的时间复杂度是 O(m)，仍然没有降到 O(1)。为了将每次检索的时间复杂度降到 O(1)，需要使用二维前缀和，在初始化的时候计算二维前缀和数组。

做这种初始化一次、检索多次的题目的秘诀：在初始化的时候做预处理。

2.1 求 preSum

定义 preSum[i][j] 表示 从 [0,0] 位置到 [i,j] 位置的子矩形所有元素之和。

\[S(O,D)=S(O,C)+S(O,B)−S(O,A)+D \]

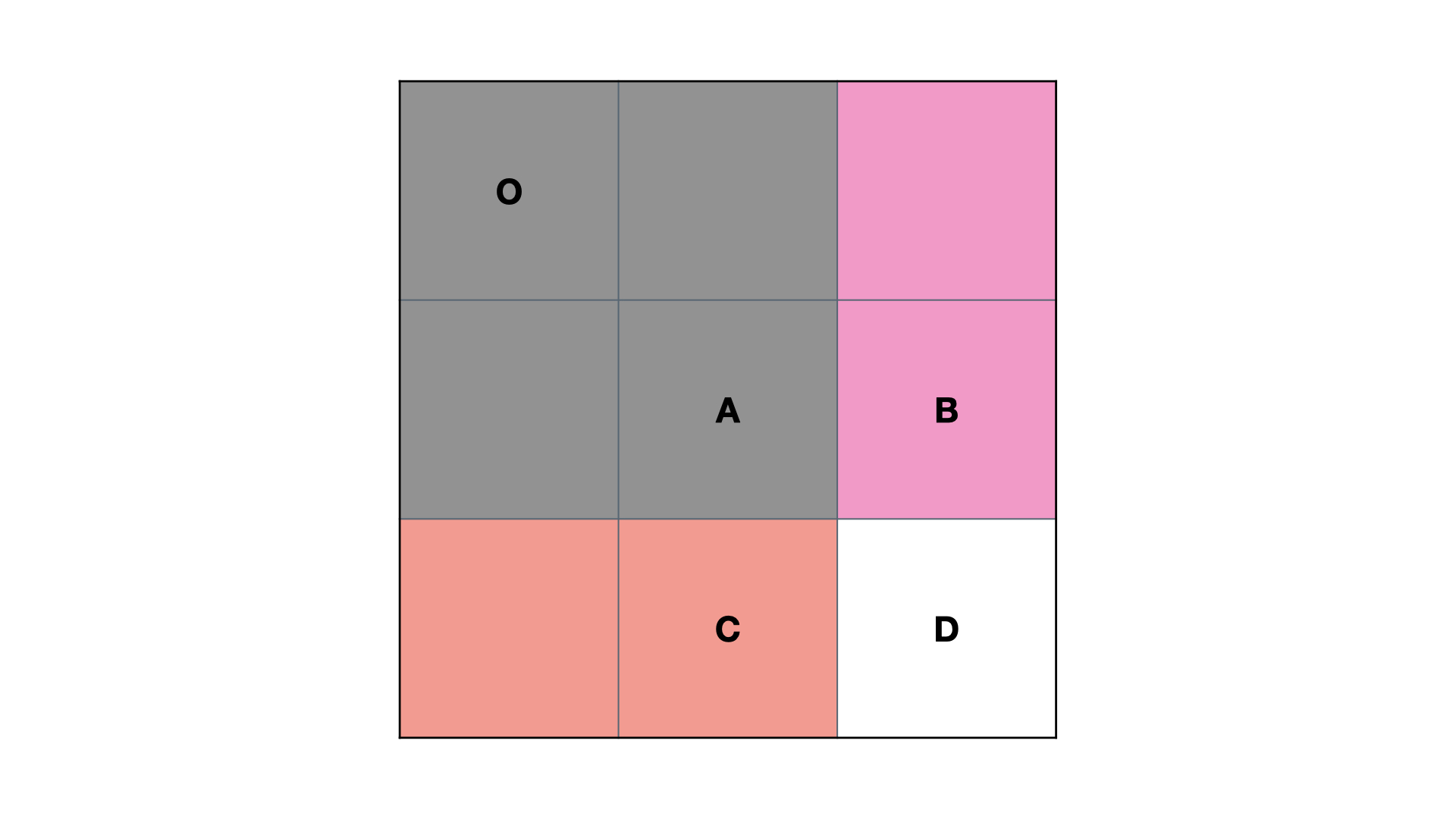
如果求 preSum[i][j] 表示的话，对应了以下的递推公式：

\[preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i][j] \]

2.2 根据 preSum 求子矩形面积

\[S(A,D)=S(O,D)−S(O,E)−S(O,F)+S(O,G) \]

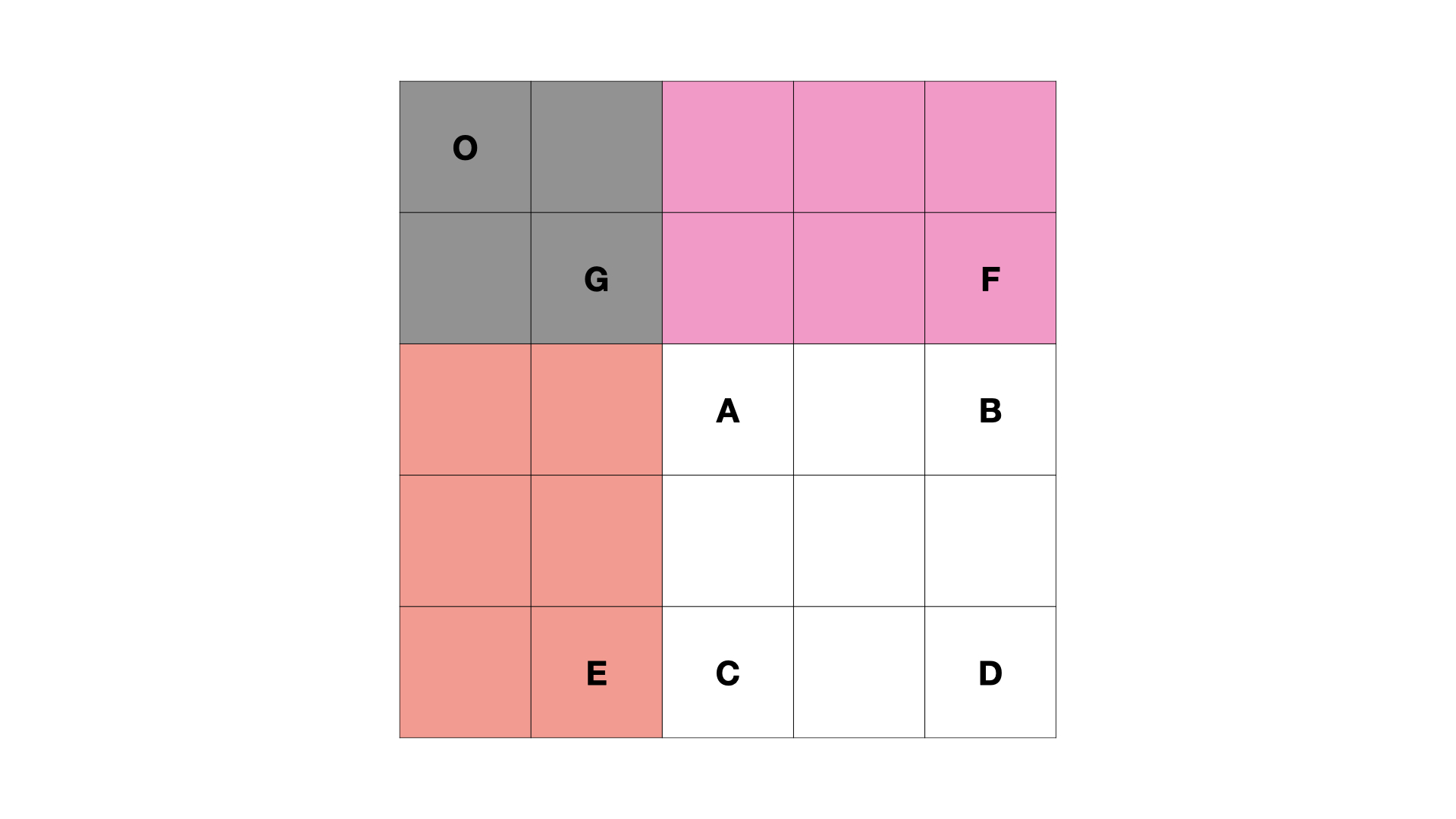
如果要求 [row1, col1] 到 [row2, col2] 的子矩形的面积的话，用 preSum 对应了以下的递推公式：

\[preSum[row2][col2] - preSum[row2][col1 - 1] - preSum[row1 - 1][col2] + preSum[row1 - 1][col1 - 1] \]

下面代码实现的时候，使用的 preSum 比原矩阵 matrix 多了一行一列，是为了让第 0 行与第 0 列的元素也能使用上面的递推公式。如果 preSum 矩阵大小和 martix 大小相等，则需要对第 0 行与第 0 列特殊判断。

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        if not matrix or not matrix[0]:
            M, N = 0, 0
        else:
            M, N = len(matrix), len(matrix[0])
        self.preSum = [[0] * (N + 1) for _ in range(M + 1)]
        for i in range(M):
            for j in range(N):
                self.preSum[i + 1][j + 1] = self.preSum[i][j + 1] + self.preSum[i + 1][j]  - self.preSum[i][j] + matrix[i][j]


    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.preSum[row2 + 1][col2 + 1] - self.preSum[row2 + 1][col1] - self.preSum[row1][col2 + 1] + self.preSum[row1][col1]

作者：fuxuemingzhu
链接：https://leetcode.cn/problems/range-sum-query-2d-immutable/solution/ru-he-qiu-er-wei-de-qian-zhui-he-yi-ji-y-6c21/。

时间复杂度：初始化 O(mn)，每次检索 O(1)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。初始化需要遍历矩阵 matrix 计算二维前缀和，时间复杂度是 O(mn)。每次检索的时间复杂度是 O(1)。
空间复杂度：O(mn)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。需要创建一个 m+1 行 n+1 列的二维前缀和数组 preSum。