【多重集合和映射】力扣332：重新安排行程（附回溯框架）()

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。
所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票必须都用一次且只能用一次。

示例：

输入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出：["JFK","ATL","JFK","SFO","ATL","SFO"]
解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠后。

化简题意：给定一个 n 个点 m 条边的图，要求从指定的顶点出发，经过所有的边恰好一次（可以理解为给定起点的「一笔画」问题），使得路径的字典序最小。
这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系：

通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路
通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路
具有欧拉回路的无向图称为欧拉图
具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图

由于题目中说必然存在一条有效路径，那么这张图是一个欧拉图或者半欧拉图，所以算法不需要回溯（即加入到结果集里的元素不需要删除）。

整个图最多存在一个死胡同(出度和入度相差1），且这个死胡同一定是最后一个访问到的，否则无法完成一笔画
- 如果没有保证至少存在一种合理的路径，需要判别这张图是否是欧拉图或者半欧拉图：
  - 对于无向图 G，G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。
  - 对于无向图 G，G 是半欧拉图当且仅当 G 是连通的且 G 中恰有 0 个或 2 个奇度顶点。
  - 对于有向图 G，G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
  - 对于有向图 G，G 是半欧拉图当且仅当
    - 如果将 G 中的所有有向边退化为无向边时，那么 G 的所有顶点属于同一个强连通分量；
    - 最多只有一个顶点的出度与入度差为 1；
    - 最多只有一个顶点的入度与出度差为 1；
    - 所有其他顶点的入度和出度相同。
DFS的调用其实是一个拆边的过程（既每次递归调用删除一条边，所有子递归都返回后，再将当前节点加入结果集保证了结果集的逆序输出），一定是递归到这个死胡同（没有子递归可以调用）后递归函数开始返回。所以死胡同是第一个加入结果集的元素
最后逆序输出即可

既然要求字典序最小，那么每次就应该贪心地选择当前节点所连的节点中字典序最小的那一个，并将其入栈。最后栈中就保存了遍历的顺序。

当贪心地选择字典序最小的节点前进时，可能先走入「死胡同」，从而导致无法遍历到其他还未访问的边。于是希望能够遍历完当前节点所连接的其他节点后再进入「死胡同」

为了保证能够快速找到当前节点所连的节点中字典序最小的那一个，可以使用优先队列存储当前节点所连到的点，每次 O(1) 地找到最小字典序的节点，并 O(logm) 地删除它。

1. 深度优先搜索
Hierholzer 算法用于在连通图中寻找欧拉路径，流程如下：

从起点出发，进行深度优先搜索 (DFS)
每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边
如果没有可移动的路径，则将所在节点加入到栈中，并返回

当顺序地考虑该问题时，无法判断当前节点的哪一个分支是「死胡同」分支。不妨倒过来思考。注意到只有那个入度与出度差为 1 的节点会导致死胡同，而该节点必然是最后一个遍历到的节点。可以改变入栈的规则，遍历完一个节点所连的所有节点后，才将该节点入栈（即逆序入栈）。

对于当前节点而言，从它的每一个非「死胡同」分支出发进行深度优先搜索，都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说，当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。

这样就能保证「一笔画」地走完所有边，最终的栈中逆序地保存了「一笔画」的结果。只要将栈中的内容反转，即可得到答案。

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        def dfs(curr: str):
            while vec[curr]:
                tmp = heapq.heappop(vec[curr])
                dfs(tmp)
            stack.append(curr)

        vec = collections.defaultdict(list)
        for depart, arrive in tickets:
            vec[depart].append(arrive)
        for key in vec:
            heapq.heapify(vec[key])

        stack = list()
        dfs("JFK")
        return stack[::-1]

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/reconstruct-itinerary/solution/zhong-xin-an-pai-xing-cheng-by-leetcode-solution/

时间复杂度：O(mlogm)，其中 m 是边的数量。对于每一条边需要 O(logm) 地删除它，最终的答案序列长度为 m+1，而与 n 无关。
空间复杂度：O(m)，其中 m 是边的数量。需要存储每一条边。

简介代码详细解析

import collections

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:

        # 核心思想--深度搜索 + 回溯
        # 首先先把图的邻接表存进字典，然后对字典的value进行排序
        # 然后从'JFK'开始深搜，每前进一层就减去一条路径
        # 直到某个节点不存通往其他节点的路径时，说明该节点就为此次行程的终点
        # 需要跳出while循环进行回溯，返回到上一层节点进行搜索，再次找到倒数第二个终点，依次类推
        # 设定ans为返回答案，每次找到的节点都要往头部插入

        # 举例说明：[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
        # 构建领接表的字典：{'JFK': ['SFO', 'ATL'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})
        # 按照题目要求对字典的val排序：{'JFK': ['ATL', 'SFO'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})
        # 开始从 JFL 开始进行dfs搜索
        # 1.JFK --> ALT  
        #   JFK pop出ALT,JFK的字典变为：'JFK': ['SFO']
        # 2.JFK --> ALT --> JFK 
        #   ALT pop出JFK,ALT的字典变为：'ALT': ['SFO']
        # 3.JFK --> ALT --> JFK --> SFO 
        #   JFK pop出SFO,JFK的字典变为：'JFK': ['']
        # 4.JFK --> ALT --> JFK --> SFO --> ATL 
        #   SFO pop出ALT,SFO的字典变为：'SFO': ['']
        # 5.JFK --> ALT --> JFK --> SFO --> ATL --> SFO
        #   ATL pop出SFO,ATL的字典变为：'ATL': ['']
        # 此时我们可以发现SFO的val为空，没有地方可以去了，说明我们已经找出了终点SFO
        # 然后向上回溯，依次将其添加到ans中
        # 最终答案为：["JFK","ATL","JFK","SFO","ATL","SFO"]


        d = collections.defaultdict(list)   #邻接表
        for f, t in tickets:
            d[f] += [t]  # 路径存进邻接表

        for f in d:
            d[f].sort()  # 邻接表排序

        ans = []
        def dfs(f):  # 深搜函数
            while d[f]:
                dfs(d[f].pop(0))  # 路径检索
            ans.insert(0, f)  # 放在最前

        dfs('JFK')
        return ans

作者：charlesd
链接：https://leetcode.cn/problems/reconstruct-itinerary/solution/332-zhong-xin-an-pai-xing-cheng-chao-xiang-xi-ti-j/

2. 回溯算法
首先把回溯算法的框架写出来

    def findItinerary(self, tickets):
        path = [] # 记录路径
        # res = [] # 多条路径，记录结果
        def backtrack(cur):

            if # 结束条件:
                # res.append(path[:])
                return True

            for 某节点 in 当前节点可以有的选择:
                # 去掉不合适选择
                path.append(某节点)  # 做选择
                if backtrack(某节点):  # 进入下一层决策树
                    return True
                path.pop()  # 取消选择

            return False
        backtrack(cur)
        return path

作者：yun-yi-hen
链接：https://leetcode.cn/problems/reconstruct-itinerary/solution/pythonhui-su-suan-fa-ji-bai-9523-by-yun-yi-hen/

本题的结束条件：遍历完所有路径，path的长度为字符串二维数组长度 + 1
循环结构：每次取出某节点后，将这个节点从备用选择中删除，防止出现循环路径
用字典把对应的机场位置存储起来，变成如图所示的状态，然后就好求解了：

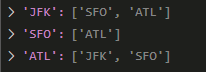
[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]

class Solution:
    def findItinerary(self, tickets):
        from collections import defaultdict
        ticket_dict = defaultdict(list)
        for item in tickets:
            ticket_dict[item[0]].append(item[1])

        path = ['JFK']

        def backtrack(cur_from):
            if len(path) == len(tickets) + 1:  # 结束条件
                return True
            ticket_dict[cur_from].sort()
            for _ in ticket_dict[cur_from]:
                cur_to = ticket_dict[cur_from].pop(0)  # 删除当前节点
                path.append(cur_to)  # 做选择
                if backtrack(cur_to):  # 进入下一层决策树
                    return True
                path.pop()  # 取消选择
                ticket_dict[cur_from].append(cur_to)  # 恢复当前节点
            return False

        backtrack('JFK')
        return path

作者：yun-yi-hen
链接：https://leetcode.cn/problems/reconstruct-itinerary/solution/pythonhui-su-suan-fa-ji-bai-9523-by-yun-yi-hen/

posted @ 2022-06-20 20:09 Vonos 阅读(152) 评论(0) 收藏举报

刷新页面返回顶部

Jojo-L

【多重集合和映射】力扣332：重新安排行程（附回溯框架）()

公告