【哈希表】力扣149:直线上最多的点数(未完)
给你一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
示例:
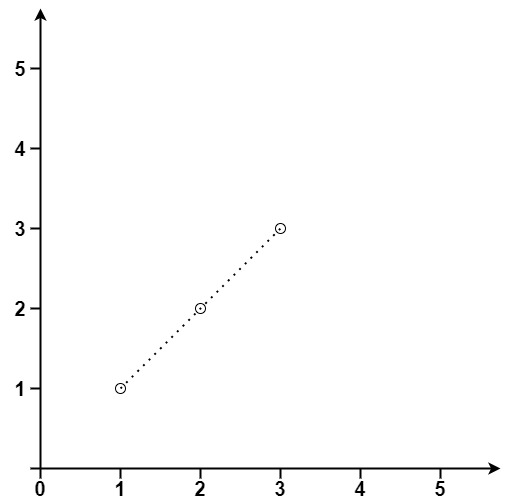
输入:points = [[1,1],[2,2],[3,3]]
输出:3
原理:两个点可以确定一条线;一条线可以由一个点和斜率而唯一确定。
对于每个点,对其它点建立哈希表(键为斜率,值是这个直线拥有的点数),统计同一斜率的点一共有多少个(可以使用 Counter 直接统计各个直线拥有的点数)。另外也要考虑斜率不存在和重复坐标的情况。
小技巧1:在遍历每个点时,对于数组中位置 i 的点,只需要考虑 i 之后的点即可,因为 i 之前的点已经考虑过 i 了。
小技巧2:如果点数小于 3 个,直接返回点数(因为肯定能组成直线)。
时间复杂度:O(n^2 ×logm),其中 n 为点的数量,m 为横纵坐标差的最大值。最坏情况下需要枚举所有 n 个点,枚举单个点过程中需要进行 O(n) 次最大公约数计算,单次最大公约数计算的时间复杂度是 O(logm)。
空间复杂度:O(n),其中 n 为点的数量。主要为哈希表的开销。
一行代码:
分步代码利用生成器构造一下
from collections import Counter
class Solution:
def maxPoints(self, points: List[List[int]]) -> int:
return max(sum(1 for j in points if j == i) + Counter([float('Inf') if i[1] - j[1] == 0 else (i[0] - j[0]) / (i[1] - j[1]) for j in points if j != i]).most_common(1)[0][1] if sum(1 for j in points if j == i) != len(points) else sum(1 for j in points if j == i) for i in points) if len(points) > 2 else len(points)
作者:qsctech-sange
链接:https://leetcode.cn/problems/max-points-on-a-line/solution/yi-xing-sang-xin-bing-kuang-de-yi-xing-liu-jie-fa-/
不用哈希表的枚举统计:
@ Java
class Solution {
public int maxPoints(int[][] ps) {
int n = ps.length;
int ans = 1;
for (int i = 0; i < n; i++) {
int[] x = ps[i];
for (int j = i + 1; j < n; j++) {
int[] y = ps[j];
int cnt = 2;
for (int k = j + 1; k < n; k++) {
int[] p = ps[k];
int s1 = (y[1] - x[1]) * (p[0] - y[0]);
int s2 = (p[1] - y[1]) * (y[0] - x[0]);
if (s1 == s2) cnt++;
}
ans = Math.max(ans, cnt);
}
}
return ans;
}
}
作者:AC_OIer
链接:https://leetcode.cn/problems/max-points-on-a-line/solution/gong-shui-san-xie-liang-chong-mei-ju-zhi-u44s/
思维很清晰的超多代码答案:
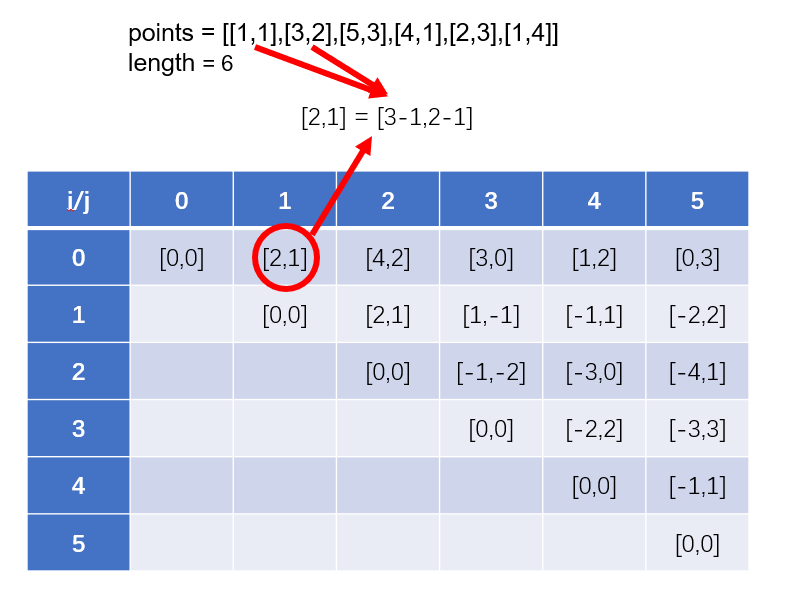
建立一个 length * length 长度的二维数组存储从第 i 个点到第 j 个点的斜率,斜率用 [x1-x0,y1-y0] 进行存储,只需要遍历这个表中同行斜率最多的相同元素个数即可。
- i到j的斜率填表:
![image]()
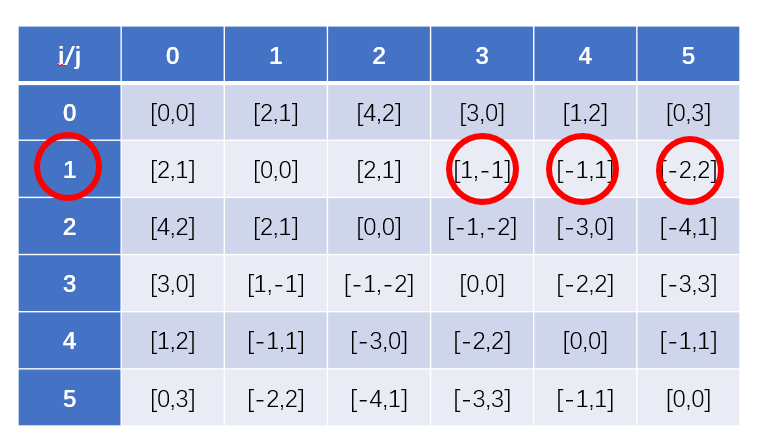
- 对称元素补表:
![image]()
- 找出一行中出现次数最多的斜率:加上点自己本身就是可连接点的个数
![image]()
class Solution:
def is_same(self,slope1,slope2): # 判断斜率是否相同
if slope1[1] == 0 and slope2[1] == 0 and slope2[0]!=0: #如果两个斜率均为正无穷(竖着的直线)并且第二个点不是第i个点
return True
elif slope1[1] == 0 or slope2[1] == 0: #如果有一个斜率为正无穷,那么直接返回False
return False
else:
if slope1[0]/slope1[1] == slope2[0]/slope2[1]: #斜率相同返回True
return True
else:
return False
def maxPoints(self, points: List[List[int]]) -> int:
length = len(points) #length为点的个数
if length == 1: #如果只有一个点,直接返回1
return 1
slope = [[[0,0]for i in range(length)]for i in range(length)] # 存储斜率 [x,y] 斜率 x/y
for i in range(length):
for j in range(i+1,length):
slope[i][j][0] = points[j][0] - points[i][0]
slope[i][j][1] = points[j][1] - points[i][1]
# 获取斜率 [x,y] x = x1 - x0, y = y1 - y0 ,slope[i][j]表示从点i到点j的斜率
set = 1
for i in range(length): # i到j的斜率和j到i的斜率相同,把表填写完整
for j in range(set):
slope[i][j] = slope[j][i]
set += 1
#接下来就是查找每行出现最多相同斜率的个数即可,就是本题答案
count = 0
for i in range(length):
for j in range(length):
if i == j:
continue
else:
flag = 1
for k in range(length):
if self.is_same(slope[i][j],slope[i][k]):
flag += 1
if flag > count:
count = flag
return count
作者:superzyc
链接:https://leetcode.cn/problems/max-points-on-a-line/solution/python-cun-chu-xie-lu-jin-xing-pan-duan-g6j4n/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号